Miből állnak az atommagok? Ha megmérjük a tömegüket és töltésüket, rájövünk, hogy azok nem függetlenek. Arra jutunk, hogy az atommag pozitív elektromos töltésű protonokból és semleges neutronokból áll. Atommagokat ütköztetve egymásnak, protonokat és neutronokat szakíthatunk ki, így megmérhetjük azok tulajdonságait is. Rájövünk, hogy nem elég összeadni az alkotók tömegét, a kölcsönhatásukat is figyelembe kell venni. Az így fejlődő modellünkkel ezután megjósolhatjuk milyen mag keletkezne, ha protonokat és neutronokat kevernénk össze. Egy szinttel lejjebb is feltehetnénk az eredeti kérdést: miből áll a proton? Hasonlóan, eljutunk a kvarkokhoz és gluonokhoz, de ezeknél a részecskéknél komoly problémába ütközünk.
Képzeljünk el azt a kiforgatott helyzetet, hogy milyen lenne, ha ismernénk a protonokat, neutronokat, sőt a kölcsönhatásukat is, azonban az atommagokat mégsem tudnánk az elmélettel felépíteni. Nem tudnánk mondjuk megjósolni, hogy milyen atommagot kapnánk, ha két protont és három neutront kevernénk össze. Még kellemetlenebb lenne, ha már a kvarkokat, gluonokat is ismernénk, de az atommagok kialakulását még mindig nem tudnánk kiszámolni. Szerencsére az atommagokra ez nincs így, de egy szinttel lejjebb, a kvarkokkal már igen. Nem tudjuk hogyan állnak össze a kvarkok protonná. Előfordulnak efféle buborékok egy elméletben: látszólag minden tapasztalatot meg tud magyarázni, bonyolultakat is, viszont ,,egyszerű” problémák magyarázata mégis hiányzik. A 2000-ben, Millenniumi problémák néven a 7 legfontosabb megoldatlan, ehhez hasonló problémát gyűjtötték össze. Többségük matematikai, fizikai, de van köztük informatikai is. A kvarkokra vonatkozó probléma a ,,Yang–Mills elméletek tömegugrása”, ami a részecskék kvarkokból való összeállásának folyamatát magyarázná meg. Erről lesz szó a továbbiakban.
A kvantumszíndinamika
A hadronokat a kisebb kvarkok és gluonok alkotják. Ilyen például a proton és a neutron is. Az elektronban ezzel szemben nincsenek kvarkok, így az elemi részecske. A kvarkokat, gluonokat és a köztük lévő kölcsönhatást leíró elmélet a kvantumszíndinamika. Az elmélet szerint a kvarkoknak és gluonoknak színtöltésük van, ami nagyon hasonló az elektromos töltéshez, de háromféle van belőle: piros és antipiros, zöld és antizöld, valamint kék és antikék, tehát minden pozitív-negatív töltéshez tartozik egy szín is. Jelenleg 6-féle kvarkot ismerünk: u, d, s, c, b és t-kvarkot. A kvantumszíndinamikát már a 60-as évek óta ismerjük és használjuk, sőt az elmélet jóslatait naponta tesztelik, az olyan kísérleti eszközök, mint a CERN Nagy Hadronütköztetője (az LHC), vagy az amerikai Relativisztikus Nehézion Ütköztető (a RHIC). Eddigi tapasztalataink alapján mondhatjuk, hogy jól ismerjük az elméletet, és jól is működik, noha önmagában egy darab kvarkot vagy gluont sem sikerült megfigyelnünk. A fenti példánál maradva, meg tudjuk csinálni, hogy kilökünk az atommagból egy protont és megvizsgáljuk, annak az egynek a méretét, tömegét vagy az elektromos töltését. A kvarkokkal és gluonokkal ezt nem tudtuk megtenni, sőt a kvantumszíndinamika azt jósolja, hogy ez nem is lehetséges. Az elmélet szerint a kvarkok csak párban vagy csoportban figyelhetők meg. Ha megpróbálnánk egy kvarkot erővel kivenni egy proton belsejéből, a vákuum új kvark és antikvark párt hozna létre a távolodás helyén és végül egy összetett kvark-antikvark pár maradna a kezünkben. A folyamat elképzelésére látunk egy példát a 4. ábrán. Tehát a vizsgálni kívánt kvarkunk egy összetett részecskébe, hadronba záródik. Ezt a jelenséget nevezzük kvarkbezárásnak, míg magát a folyamatot hadronizációnak.
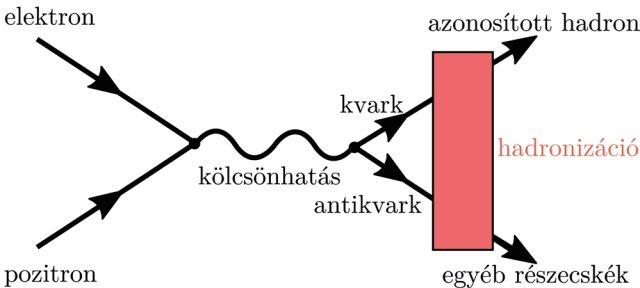
Bár nem tudjuk a kvarkokat és gluonokat önmagukban vizsgálni, bizonyíthatjuk, hogy léteznek. Részecskegyorsítókkal elektronokat lőttek a sokkal nagyobb méretű protonokra, amelyek visszapattanásáról kiderült, hogy a proton nem gömbszerű, hanem kis csomók vannak benne, a három kvark: két u és egy d-kvark. Nem tudjuk, hogy miért nem figyelhetők meg a kvarkok és gluonok önmagukban, de ez nem jelenti azt, hogy rossz az elméletünk. Például azt sem tudjuk, hogy a gravitáció miért vonz és sosem taszít, mégis tudjuk miként épül fel egy galaxis. Az alapkutatások feladata éppen az ilyen elvont kérdések tisztázása.
A kvarkok és gluonok megismeréséhez részecskéket gyorsítunk és ütköztetünk össze: elektronokat, protonokat, vagy nagyobb, arany és ólom atommagokat. Ha ezt elég nagy energiával tesszük, akkor az atommagokból, protonokból és neutronokból kvarkok és gluonok szakadnak ki, információt adva a kölcsönhatásaikról. A kiszakadt kvarkok a kvarkbezárás miatt a vákuumból még több kvark-antikvark párt keltenek és hadronokká állnak össze, vagyis hadronizálnak. Ez alól még nem láttunk kivételt, mondjuk egy ott maradt kvarkot a detektorban. A kvantumszíndinamika jósolja a kvarkbezárást, azonban annak pontos folyamatát, a hadronizációt máig nem sikerült az első törvényekből származtatni. Nem tudjuk megmondani például, hogy egy adott kvark pontosan milyen hadronba fog záródni, vagy mi határozza ezt meg. Ez egy kellemetlen helyzet, mivel a részecskefizikát leíró Standard Modellel, ami a kvantumszíndinamika mellett a részecskék minden más kölcsönhatását tartalmazza, ennél sokkal de sokkal bonyolultabb folyamatokat is ki tudunk számolni és mérésekkel igazolni. Mégis, ezt az elemi folyamatot nem tudjuk leírni. Emiatt került be a probléma a Milleniumi problémák közé.
Természetesen, az utóbbi évtized felfedezéseihez, mint például a Higgs-részecskéhez szükség volt olyan információkra, hogy miként formálják meg a kvarkok a hadronokat, emiatt a részecskefizikusok modelleket dolgoztak ki, hogy közelítsék a valóságot. Ez azonban nem oldotta meg az eredeti problémát. Olyan ez, mintha látnánk, hogy víz gyűlik fel a hajónk alján, a lyukat is látnánk, de folt híján csak a vizet mernénk ki.
A kvantumszíndinamikáról és annak határairól tovább tájékozódhatunk a Természet Világa és a Fizikai Szemle lapokban, valamint az Atomcsill online elérhető előadásaiból (http://www.atomcsill.elte.hu/).
A hadronizáció
A hadronizációt leíró modelleknek két nagy csoportja van: az egyikben csak a statisztikáját írjuk le a bezáródás folyamatának, például azt, hogy mekkora valószínűséggel záródik egy bizonyos típusú kvark – mondjuk u-kvark – a protonba vagy valamilyen más hadronba. Más modellek egyszerűsítik a kvarkok kölcsönhatásait, így ki lehet számolni belőlük, hogy egy adott kvark hogyan formál meg egy hadront. Mindkét megközelítés gyengesége, hogy szorosan nem a kvantumszíndinamikához kapcsolódnak, további plusz feltételezések vannak bennük és kísérleti adatok kellenek ahhoz, hogy beállítsák az elmélet paramétereit, amelyek száma nem kevés. Ezek segítségével viszont olyan dolgokat lehet kiszámolni, hogy milyen típusú hadronok keletkeznek az ütközés során, és milyen ezen a típusok aránya, amelyeket mérésekkel tesztelhetünk. Ideális esetben ezeket a kvantumszíndinamika első törvényeiből kellene tudnunk meghatározni.
Statisztikus leírás
A statisztikus leírás során nem arra vagyunk kíváncsiak, hogy mi a kvarkok bezáródásának pontos folyamata, csupán a lehetséges kimenetelek valószínűségére. Például arra, hogy egy adott típusú kvark vagy gluon, mekkora valószínűséggel fog valamilyen hadronba záródni. Ezeket a valószínűségeket nem tudjuk kiszámolni a kvantumszíndinamikából, de becslést tudunk rájuk adni. Például, a kvarkok nagyobb valószínűséggel záródnak olyan hadronba, ami két kvarkból áll, mint abba, ami háromból, hiszen a kvarkok egy párt könnyebben találnak, mint kettőt. Tudjuk azt is, hogy nagyobb tömegű részecskéket nehezebb létrehozni a vákuumból, mint könnyűeket, így azt várjuk, hogy a nehezebb kvarkok, mint c, b vagy t-kvark kevesebbszer fog előfordulni, így azok a hadronok is, amelyekben ilyen kvarkok vannak. Ezeket a sejtéseket igazolják a kísérleti eredmények. Leggyakrabban pionokat (u és d-kvark keveréke) és kaonokat (d és s-kvark keveréke) találnak. Ezek a legkönnyebb kvarkokat és azokból is csak kettőt tartalmaznak. A protonokban és neutronokban három-három kvark van (uud és udd), így jóval ritkábbak, ahogy a J/ψ nevű részecske is (c és anti-c keveréke), ami két nehéz kvarkot tartalmaz. Logikus kérdés, hogy ha a pionokat és kaonokat egyszerűbb létrehozni az ütközésekben, akkor a világunkat miért a protonok és neutronok építik fel? Ez azért van, mert a pion és kaon nem stabil részecske, kevesebb, mint egymilliomod másodperc alatt bomlanak el, míg a proton jelen tudásunk szerint stabil.
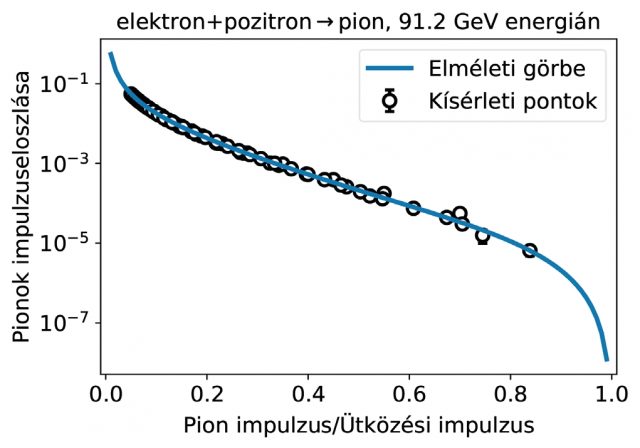
Ha elég nagy energiával elektront és pozitront ütköztetünk össze (1. ábra), a vákuumból kvarkok keletkeznek. A hadronizáció miatt ezek a kvarkok hadronokba záródnak, amelyek típusát és a típusok arányát kísérletileg mérhetjük. Más részről a Standard Modell segítségével ki tudjuk számolni, hogy kísérletben mért eredményeket. Minél kevesebb paramétert tartalmaz a modellünk, ami jól adja vissza a kísérleti eredményeket, annál jobb. A leggyakoribb ilyen eloszlások 3 paramétert tartalmaznak, így pion esetén a 6-féle kvark plusz a gluon, egyenként 3, összesen (6+1)×3=21 paramétert ad, amit be kell állítani. Különböző, megfontolásokkal csökkenteni lehet a paraméterek számát 15 körülire, például az elektromos töltés és a kvarkok típusának szimmetriáinak figyelembevételével. Hasonló mennyiségű paraméter kell kaonra, protonra vagy egyéb hadronra. Ez nagyon sok paraméter, viszont a meghatározásuk után meg tudjuk mondani, hogy mekkora valószínűséggel, mi fog történni az ütközés után.
A paraméterek ismeretében kiszámolhatjuk azt, hogy az elektron-pozitron ütközésben keletkezett pionoknak mi lesz az impulzus szerinti eloszlása, ami a 2. ábrán látható. Az elméleti görbe a beállított paraméterekkel láthatóan jól adja vissza a kísérletileg mért adatokat.
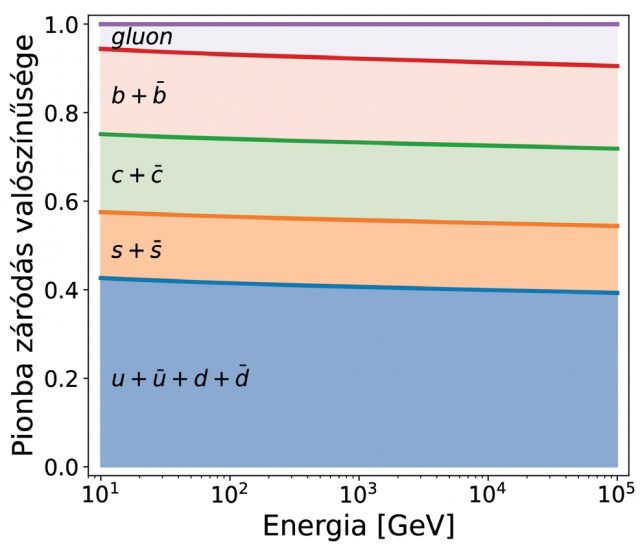
Érdekes mennyiség, amit kiszámolhatunk a valószínűségi eloszlások segítségével, hogy egy adott hadronba mekkora valószínűséggel záródik egy kvark. Ha a valószínűségi leírásunk jól működik, akkor azoknak a kvarkoknak lesz a legnagyobb járuléka, amelyek eleve a hadront alkotják. A kvantumszíndinamika azt jósolja, hogy ezeken kívül, a hadronokban más kvarkok is jelen lehetnek, igaz nagyon rövid ideig, mint egy zajos háttér. A 3. ábrán a kvarkok pionba záródásának valószínűségei láthatók összeadva, különböző energiákon. Az ábra teteje az 1-nél van, hiszen összességében a kvarkoknak és a gluonok a pion 100%-át adják. Tudjuk, hogy a piont u és d-kvark építi fel és látható, hogy összességében ezek adják a legnagyobb járulékot. Az is látható, hogy a felépítő kvarkokon kívül más kvarkok is jelen vannak, sőt nehéz kvarkok és a gluon is. Az is látható, hogy ezeknek az arányoknak gyenge az energiafüggése.
Az ábrák elkészítéséhez az egyik legnépszerűbb statisztikus modellt használtam alapul, amelynek eredményei online elérhetők (http://research.kek.jp/people/kumanos/ffs.html). A durhami egyetem minden részecskefizikai kísérlet eredményét összegyűjtötte online, amiket egy új projekt részeként szabadon vizsgálhatunk, és ábrázolhatunk online (https://hepdata.net). Innen vannak a kísérleti pontok a 2. ábrán.
Dinamikai leírás
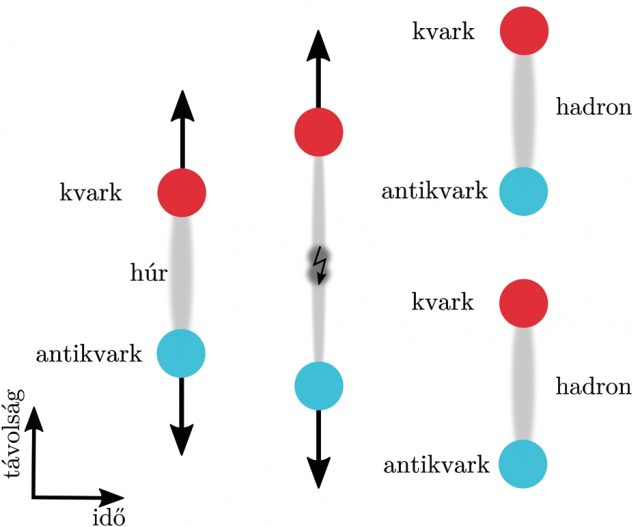
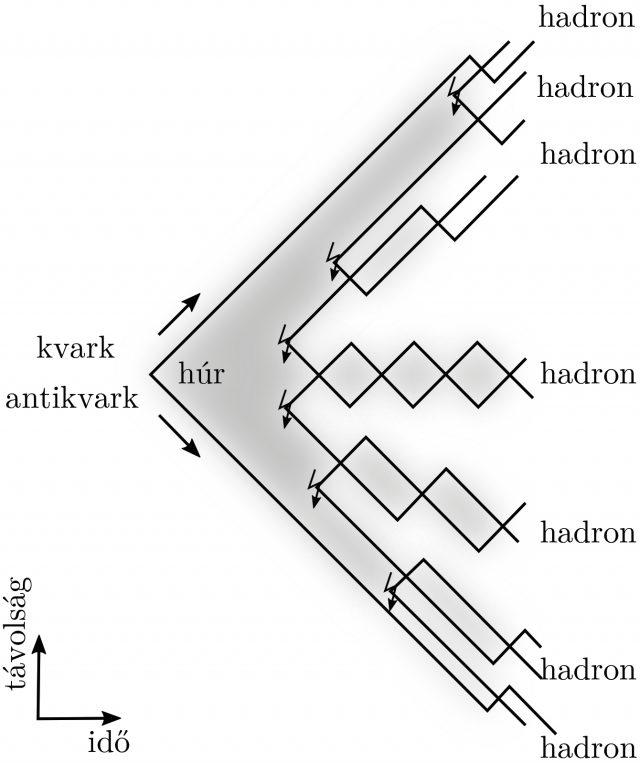
A hadronizáció leírásának egy másik típusa az, amikor a kvarkok és gluonok között valamilyen közelítő kölcsönhatást teszünk fel az eredeti helyett, amelyből ki tudjuk számolni azokat a valószínűségeket, mint a statisztikai leírásnál. A legelterjedtebb, a húrmodell. A húrmodellnek semmi köze a húrelmélethez. Ebben a modellben azt teszik fel, hogy a kvarkok között húrok vannak, amelyek megnyúlnak, amikor a kvarkok eltávolodnak egymástól. Ha a húrban túl nagy a feszültség, elszakad és az új végpontjain egy-egy kvark antikvark keletkezik. Ha az új részrendszereknek marad elég energiája, a húrok ismét megnyúlnak és elpattannak, ha nem, a húrral összekapcsolt kvarkok hadronokba záródtak. Egy illusztráció látható a húrok elszakadásáról a 4. ábrán. A 5. ábrán egy konkrét hadronizációs folyamat látható, több szakadással, a folyamat hagyományos ábrázolásmódjában.
Ebben a modellben is kiszámolhatunk olyan mennyiségeket, amelyek kísérletileg is mérhetők, ezekkel lehet beállítani a modell paramétereit. Például a húrok erejét vagy azt, hogy milyen feszültségnél szakadnak el. A paraméterek száma nem sokkal kevesebb a statisztikai leírásnál, viszont lényeges különbség, hogy egy konkrét folyamatunk van a hadronok keltésére és bezáródására. Ismerve a paramétereket, lemodellezhetünk egy egész részecskeütközést és nyomon követhetjük miként viselkednek a kvarkok és gluonok ebben az egyszerűsített képben.
A világon néhány kutatócsoport azzal foglalkozik, hogy a részecskefizikában ismert kölcsönhatásokat beleírják egy számítógépes programba és így leszimulálják azt, amit a részecskeütközések során látnánk. Ez a módszer eltér a rácstérelméleti számolásoktól, amelyeket szuperszámítógépeken végeznek. Itt, toldozva-foltozva úgy egészítik a kódot, hogy minél jobban egyezzenek az eredményeik a kísérletekkel, és lehetőleg minél kevesebb plusz paramétert tegyenek bele. Az ilyen programokat részecskefizikai eseménygenerátornak nevezik és fontos szerepük van a kísérletek megtervezésénél: várható eredményeket tudjuk velük előre megbecsülni, hogy eléggé érzékenyek-e a műszerek ahhoz, hogy kimutassuk, amit akarunk. A legelterjedtebb a PYTHIA (http://home.thep.lu.se/~torbjorn/Pythia.html) kód, ami proton-proton ütközésekre specializálódott, míg a magyar kutatók által is fejlesztett HIJING a nehezebb atommag-atommag ütközésekre. A PYTHIA, a húrmodellt használja, de támogatja a statisztikus leírás használatát is. A programok ingyenesek, példaprogramjai között híres mérések szimulációit próbálhatjuk ki alapszintű programozási ismeret segítségével.
A hadronizáció megértése egy nyitott kérdés. Az itt bemutatott modellek csak közelítései annak, amit a kvantumszíndinamikával kellene tudnunk kiszámolni. Addig azonban, amíg a valós problémát megoldják, ezek a modellek nélkülözhetetlenek. Fontosak a kísérletek tervezésénél és az eredmények kiértékelésénél is. Mára eljutottunk odáig, hogy olyan pontosan vagyunk képesek mérni, hogy új hadronizációs modellekre van szükségünk, például a kvark-gluon plazma vizsgálatához.
![]() Köszönetnyilvánítás
Köszönetnyilvánítás
A szerző kutatásait az Emberi Erőforrások Minisztériuma Új Nemzeti Kiválóság Programja és az OTKA K120660 támogatja.
 A cikk az MTA TTK és a TIT közös ismeretterjesztő pályázatának második helyezését érte el Természet Világa kategóriában.
A cikk az MTA TTK és a TIT közös ismeretterjesztő pályázatának második helyezését érte el Természet Világa kategóriában.
A cikk a Természet Világa 2019. februári (150. évf. 02. sz.) számában jelent meg.


