„Kezdetben volt egy nagy korong,
Lent a föld lapos s fent a csillagok,
Alattunk lent az ördögök,
Felettünk fent az angyalok.Így játszadoztak az emberek,
Éltek és álmodtak, mi mást lehet?
De néhány kíváncsi ezek felett,
Valami újat keresgetett,
Mert nem hitte el, hogy nem lehet,
A korong széléig merészkedett.Hátukon egy-egy nagy hátizsák,
S csak gyűlt bele lassan az igazság,
Mely súly alatt a korong szélei
Elkezdtek lassan gömbbé hajlani.”
(Demjén Ferenc)
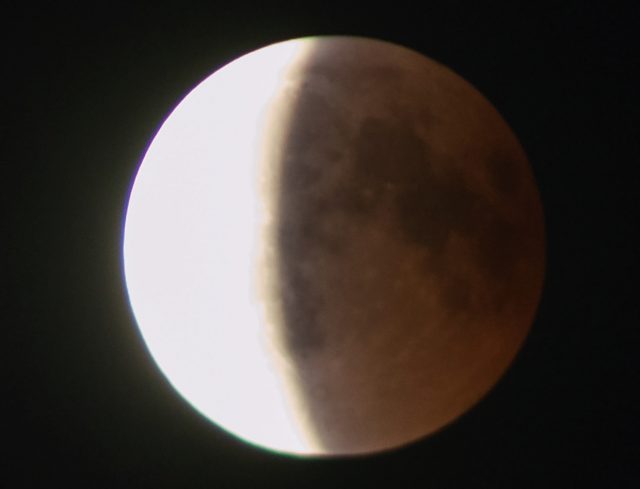
A tudós ember nem csak néz, hanem lát is. Észrevesz olyan dolgokat, amelyek szokatlanok, és úgy érzi, hogy el kell gondolkodni rajta, és késztetést érez, hogy magyarázatot is keressen rá. Az időszámításunk előtti III. évszázadban már észrevették, hogy holdfogyatkozáskor az égitest eltűnése, és felbukkanása egy ív mentén történik. Mivel az égi vándor ismét előkerült rájöttek, hogy ez a jelenség valaminek az árnyéka, a Holdat csak ideiglenesen nem látjuk. Minek az árnyéka lehet íves? Lehet lapos korong, de egy gömbnek az árnyéka is íves. Könnyen belátható mindez, ha némi geometriai ismeret birtokában megnézzük a holdfogyatkozások fényképeinek fázisait.
Egy másik megfigyelés is izgalmasnak bizonyult, két egymástól nagyon távol lévő városban, amelyek egymáshoz viszonyítva északi illetve déli irányban helyezkednek el, másképpen vet árnyékot egy gnómon.
Az is közismert volt, hogy amikor közelednek a vitorlás hajók, az árbocaik teteje látható meg először, távolodáskor pedig az tűnik el a szemünk elől utoljára. Három optikai jelenség, amely a felületes szemlélő számára nem kapcsolható össze. Eratoszthenész (Kr. e. 276 – Kr. e. 194) görög gondolkodó megtalálta a kapcsolatot, mégpedig élőhelyünk, a Föld geometriai alakját. Elegáns, a geometria szerint levezethető, bizonyítható állítást fogalmazott meg: a Föld gömb alakú! Ezzel a feltételezéssel mindhárom jelenség magyarázható.
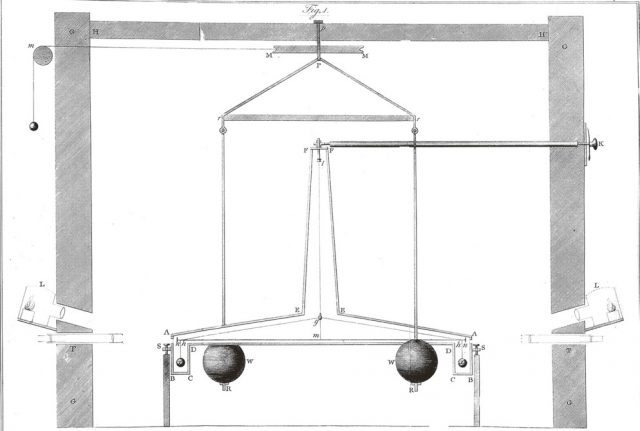
A gravitáció ismerete hiányában nehezen magyarázható, hogy a gömb alakú Föld miért vonz mindent a középpontja felé, másképpen fogalmazva miért nem esnek le róla a tárgyak. Igazán jól csak a Föld méretét ismerve lehetett megérteni mindhárom jelenséget. A kürénéi származású gondolkodó megtalálta a módszert, ami segítségével mérések alapján kiszámolta a Föld méretét, és a mai ismereteink szerinti értéktől mindösszesen 2 százalék eltéréssel határozta meg. Ha a Föld alakja mellett az átmérőjét és a tömegét is ismerjük, akkor már könnyen érthetővé válik, hogy miért nem esünk le róla, és az is, hogy miért nem tapasztaljuk hétköznapi körülmények között a tömegvonzást a körülöttünk található testek között. A gravitációnak, ennek az elvont fogalomnak a megértéshez észre kellett venni, hogy az elképesztően távoli jelenségeknek ugyanaz a magyarázata. A Hold és a lehulló alma mozgásában kellett megtalálni a közöset. Az 1687-ben megjelenő Philosophiae Naturalis Principia Mathematica, Newton műve erre is magyarázatot adott. A jelenségek leírásához először mindkét testet, a Holdat és az almát is gondolatban ponttá kellett zsugorítani. Megfigyelni azt a pályát, amit a tömegpontok bejárnak, és megtalálni köztük az összefüggést. Konkrét esetekre számolható formában adta közre a tömegvonzást leíró képletet. Az egyenletre pillantva látszik, hogy tömegpontok közötti hatást ír le, kiterjedt testek esetében integrálással juthatunk eredményre. Ez ma már a középiskolát végzetteknek kötelező tananyag, amit, ha jól sajátít el a diák, maga is kiszámolhat, ellenőrizhet. A képlet Newton idejében még nem volt teljes, a gravitációs törvényt csak arányosság formájában fogalmazta meg. Newton elmélete alapján Henry Cavendish 1797-98-ban megmérte a Föld sűrűségét, ami 5,448 ± 0,033- szorosa a vízének. Ebből az átmérő (6371 kilométer,- amit ugye már Eratoszthenész megmért az ókorban) ismeretében a Föld tömege (5,972·1024 kg) meghatározható. Kísérletéhez egy érzékeny torziós ingát használt.

A torziós szálon függő, fából készült rúd két végére két 0,73 kg tömegű testet helyezett el. Mellé, az inga karjainak végeihez 158 kg tömegű testeket tett. A kísérlet a gyenge gravitációs vonzást mérte a kis és a nagy golyók között. Az ébredő erők a torziós szálat elcsavarták, az elcsavarodás mértéke a vonzóerővel arányos. A hatás oly csekély, hogy a körülöttük lévő levegő legkisebb mozgása is meghiúsította volna a mérést, így a mérleget egy zárt dobozban, az egész összeállítást pedig egy házikóban helyezte el. A torziós inga elcsavarodása oly kicsiny volt, hogy a megmérése nem vezetett volna eredményre. Érzékenyebbé tehető a mérés, ha a torziós szálon függő rúd torziós lengéseinek periódusidejét mérjük.
További fontos körülmény, hogy a mérő személynek is van tömege, így jelenléte a mérés közelében elfogadhatatlan hibát eredményezett volna. Cavendish ezért egy távcsövet épített, amivel a házikó oldalán lévő lyukakon keresztül végezte a megfigyeléseit. Pillantsunk a képletre és számoljunk egy kicsit!
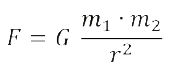
Eszerint a kisebb golyó 7,3 N erővel nyomná az asztalt. A mérés során a 158 kg tömegű test vonzása eredményeként ennek az erőnek mintegy harminchat milliomoda nagyságú vonzóerő ébred. Ezt az erőt mérte meg Cavendish, oly precízen, hogy a számításait három tizedesjegy pontossággal adhatta meg. A kiszámított átlagsűrűség sokkal nagyobb, mint a földkéregé, tehát feltételezhető, hogy bolygónknak van egy nagy sűrűségű magja. Ez kezdetben hipotézis volt, így a mérést a tézis első megerősítésnek vehetjük.
Eötvös Loránd egyetemi óráin erről a torziós ingáról tartott előadást, és a fent említett tulajdonságokat sorolva fogalmazódott meg benne a továbbfejlesztés lehetősége. Nem csak a mérő személy tömege lehet hatással a torziós ingára, hanem a körülötte lévő tárgyak mindegyike. Eötvös laboratóriuma Budapesten a mai Puskin utcában volt. A továbbfejlesztett torziós inga képes volt a Duna vízszintjének megmérésére, pedig a folyam majdnem egy kilométerre található a laboratóriumtól. Az ingák képesek mind vízszintes, mind függőleges irányban mérni. Így lettek arra alkalmasak, hogy belássanak a Föld felszíne alá és számot adjanak az eltérő sűrűségekről.
Több mint 2200 év telt el Eratoszthenész mérése óta, olyan műszerek, eszközök birtokába jutottunk, amelyek még az ötven évvel előttünk élt emberek számára is elképzelhetetlenek. A Föld alakját illetően nem maradhat kétely az iskolát végzett ember számára. És mégis úgy látszik, vannak, akik megingathatatlanul hisznek abban, hogy Földünk egy lapos korong, amely nyugalomban van, és szilárd kupolaként borul fölé az ég. Ez a bronzkori eredetű nézet jelenik meg a Bibliában is.


Napjainkban reneszánszát éli a lapos Föld „elmélet”, melynek akadnak magyar követői is. A Lapos Föld Társaság (Flat Earth Society) megalakulásakor (1849) a Biblia szó szerinti értelmezése alapján kezdte hirdetni e szemléletet. Napjainkban már nem a Bibliában olvasottakra hivatkoznak, hanem a tudományt hívják segítségül. Érvelésükkel csak természettudományokban járatlanokat tudnak elbizonytalanítani, megtéveszteni. A vélekedés terjedését nagymértékben köszönhetjük a nyomtatott és elektronikus médiumokban dolgozó „híresztelőknek”, akik nem értik a tudomány működését, vagy csak a szenzáció és a nézettség lebeg munkájuk közben a szemük előtt. Sajnos azt a látszatot keltik, hogy tudományos cikket olvasunk, tudományos vita nézői, hallgatói vagyunk. A megjelenés nem azt sugallja, hogy áltudományról, hiedelemről, vagy vallási meggyőződésről van szó, hanem egy-egy lehetséges elmélet tudósai vitatkoznak. Egyenrangúnak állítja be a cikk szerzője, a műsor készítője a laposföld nézet terjesztőjét, a tudománnyal, annak képviselőjével. Ilyen műsorba elmenni, ott megszólalni tudósként, egyet jelent azzal, hogy a másik oldalt elismerjük tudományként. Nem szabad alábecsülni ezek hatását, főleg, hogy a közösségi médiumokban az ilyen bombasztikus hírek hihetetlen sebességgel terjednek, köszönhetően annak, hogy itt nem szükséges a terjesztőnek ellenőriztetni, szakmai körökben referáltatni a közölt információkat. Mit mondhat a hívőnek a tudomány? Mit szólna Eötvös Loránd az ilyen gondolkodásmódhoz? Tudóshoz illő módon, tényekre támaszkodna. Amit a Földről látunk, az alapján előfordulhatna, hogy a Nap és az égitestek keringenek a Föld körül. Vegyünk egy közismert példát, ülünk az álló vonaton és azt látjuk, hogy a mellettünk lévő szerelvény megmozdul, de az is lehet, hogy mi eredtünk útnak. Hogyan tudjuk meghatározni, hogy ki indult el? Például méréssel! Ha van a fülke asztalán egy pohár víz, akkor könnyű a dolgunk, meg kell figyelni a víz felszínét, ha ferde, akkor a mi vonatunk, ha vízszintes, akkor a másik szerelvény gyorsul. Vegyük észre, hogy Newton törvényeit használjuk, ezek pedig csak inerciarendszerekben érvényesek. Az inerciarendszer olyan koordináta-rendszer, amiben egy magára hagyott (más testekkel kölcsönhatásban nem levő) test egyenes vonalú egyenletes mozgást végez. Ennek analógiájára el tudjuk dönteni, hogy Földünk inerciarendszer vagy sem: ki kell mutatnunk azokat az erőket, amelyek inerciarendszerben sohasem lépnének fel. Eötvös Loránd az ingával számtalan mérést végzett, de rajta kívül is még sokan mérték a Föld gravitációs terét, és mindenkinek ugyanaz az eredmény jött ki, a Föld gömb alakú, és forog! A forgó Föld nem tekinthető inerciarendszernek. Két tehetetlenségi erővel kell számolnunk, amelyeket megmérve eldönthetjük a „vitát”. Az egyik a centrifugális erő, amely függ a forgástengelytől mért távolságtól (r), a forgási sebességtől (ω), és a tömegtől (m):
Fc = m∙ω2∙r
A Föld felszínén egy nyugvó test súlya (a nehézségi erő), a gravitációs vonzóerő és a forgó vonatkoztatási rendszerben fellépő centrifugális erő eredője. A centrifugális erő értéke az egyenlítőn éppen ellentétes irányú a Föld tömegéből eredő vonzóerővel a tömegvonzással. A képlet szerint itt a legnagyobb az r, és legkisebb a g értéke. Ha a Föld minden pontján ugyanazt az értéket mérnénk, akkor inerciarendszerben lennénk. A mérések azt mutatják, hogy az egyenlítőtől az északi és a déli sarkok felé közeledve egyre nagyobb a g értéke, vagyis a pólusokhoz közeledve a centrifugális gyorsulás értéke csökken, mégpedig éppen úgy, ahogy az ismert képletek megjósolják. Abban az esetben, ha a forgó Földön egy test mozog is, egy másik tehetetlenségi erővel, a Coriolis-erővel is számolnunk kell. Nagyságát kiszámolhatjuk az alábbi képlettel:
FCoriolis = 2∙m∙v∙ω∙sinα
ahol α a mozgásiránynak a Föld forgástengelyével bezárt szöge. A francia Foucault 1851-ben nem a Coriolis-erőt mérte meg, hanem a hatását mutatta ki híres inga kísérletében. Az inga végén lengő golyóra ható erők között megtaláljuk a Coriolis-erőt is, ennek következtében az inga lengési síkja lassan elfordul. Az a kísérletező, aki nem a párizsi Pantheont választja helyszínül, hanem attól északabbra, vagy délebbre mér, más-más elfordulási sebességet fog tapasztalni, pontosan úgy, ahogy a fizika megjósolja. Budapesten óránként 11 fok az elfordulás. Ez azt jelenti, hogy a mérés ideje hosszú lesz.

Eötvös Loránd is épített egy műszert, amely szintén képes a Föld forgását igazolni. Az 1900-as évek elején elvégzett kísérletekben szisztematikus hiba jelentkezett, amikor az Indiai- és a Csendes-óceánon haladó hajókon vizsgálták a gravitációs térerősséget. Ugyanazon a helyen keletre és nyugatra haladva eltérő értéket adtak a mérések. Ez elgondolkodtatta Eötvöst és tervezett egy csodálatos műszert a jelenség, az Eötvös-effektus kutatására. A mérőberendezés egy kettős tűcsapágyon megtámasztott rúd, két végén elhelyezett nagyobb tömegekkel. Tulajdonképpen egy speciális mérleg, amelyet a függőleges szimmetriatengelye körül lehetett forgatni. Ha az Eötvös-mérleg karja északdél irányba mutat, akkor az egyik test keletre, a másik nyugatra mozdul éppen. A keletre tartó a Coriolis-gyorsulás miatt könnyebb, a nyugatra tartó pedig nehezebb lesz. 180 fokos elfordulás után a szerepek felcserélődnek, ekkor ellentétes irányú lesz a „súlyváltozás”, a műszer billegni kezd. Eötvös a mérlegkar lengésidejét és a forgás periódusidejét összehangolta, ekkor a szinte mérhetetlenül kicsi effektus a rezonancia segítségével jól láthatóvá és mérhetővé vált. Ezzel megmutatta a szisztematikus hiba okát. Ha valaki kiszámolja, hogy a mozgás hányadik tizedesjegyben okoz eltérést, rögtön beláthatja, hogy miért szán könyvében Leon Lederman egy teljes fejezetet Eötvös Lorándnak „Egy kimondhatatlanul pontos marslakó” címmel.
Hogyan érvelhetünk az alábbi jellemző kijelentésekkel szemben?
„Az nem lehet, hogy egy labdán élsz, de nem tudod lemérni a görbületét. Járj utána te is, de légy óvatos! A tudomány nem engedi, hogy bizonyos kérdéseket feltegyél.”
Nehéz a válasz, mert aki ilyet állít, az sajnos minden bizonnyal tudományellenes nézeteket vall, ő csak a tudomány eredményeit használja anélkül, hogy tudna róla. Ha a közoktatásban szerzett tudás érték lenne a “közoktatást elszenvedők” szemében, sokkal könnyebb lenne a helyzet. Amíg nem változik ez a szemlélet, addig csak falra hányt borsó sikerességű lesz a fenti cikk megértése is.
HÄRTLEIN KÁROLY
A cikk a Természet Világa 2019. novemberi számában (150. évf. 11. sz.) jelent meg.





