KISS ÁRPÁD – PERJÉS ZOLTÁN
A gravitációs hullámok
Kevesen tudják, hogy világszerte folynak korunk legnagyobb szabású kísérleti fizikai méréseinek előkészületei. Gravitációs obszervatóriumok épülnek az Egyesült Államokban, Ausztráliában, Németországban, Olaszországban és Japánban. A cél: új ablakot nyitni az égboltra a gravitációs hullámok minden eddiginél érzékenyebb megfigyelőmódszerével. Ehhez mérhető vállalkozás a fizikában csupán a részecskefizikusok által megálmodott hatalmas ütköztető gyűrű volt, annak építését azonban az Egyesült Államok kongresszusa a túlzott költségek miatt leállította.
A gravitációs hullámok észlelésében sorsdöntő volt az 1992. év: ekkor hagyta jvá az Egyesült Államok kongresszusa a LIGO (Lézer Interferometriás Gravitációs Obszervatórium) megépítését. Az észlelések 1998-ban kezdődnek. 1993 őszén a francia és az olasz kormány jóváhagyta a VIRGO programot, amely ugyancsak az évezred végére ígéri a gravitációs hullámok kimutatását. 1993-ban pedig a fizikai Nóbel-díjat Russel Hulse és Robert Taylor a gravitációs hullámok létezését megerősítő pulzár megfigyeléseikért kapták.
Az épülő gravitációs obszervatóriumok nagyon megváltoztatják a világmindenségről alkotott elképzeléseinket. A világmindenség az optikai távcsövekben nyugodt, alig változó képet mutat; a csillagok fejlődése évmilliók alatt zajlik le. A rádiócsillagászat új vonásokkal gazdagította ezt a képet: a pulzárok rendszeresen érkező impulzusait példátlan pontossággal követik a megfigyelések. Ezekben a sűrű anyagú neutroncsillagokban a folyamatok másodpercek vagy éppen ezredmásodpercek alatt történnek. Különböző hullámhossz-tartományait észlelik: a molekulák és az atomok a gyenge gravitációjú, kis sebességű tartományokban sugározzák ki az elektromágneses információt. A gravitációs hullámok viszont az erős gravitációjú, nagy sűrűségű tartományokból erednek. A nagy energiasűrűségük miatt az ezekben a tartományokban lejátszódó jelenségek erősen befolyásolják az egész világmindenség fejlődését.
A gravitációs hullámok létét már 1915-ben kikövetkeztette Einstein az általános relativitáselméletből. A gravitáció azonban oly csekély kölcsönhatás, hogy Einstein megkockáztatta: talán soha nem sikerül a hullámok kísérleti kimutatása. Annyi bizonyos, hogy a kellő erősségű hullámok forrását a laboratóriumokon kívül, kozmikus jelenségekben kell keresni.
Gravitációs hullámok a relativitáselméletben
Einstein relativitáselmélete bevezeti a négy dimenziós téridő fogalmát. Megszűnik a tér és az idő függetlensége. Ez a szemléletmód átfogóbb, mint Newtoné, akinek a felfogása szerint az idő teljesen elkülönül a térbeli viszonyoktól.
Az általános relativitáselmélet a tömegvonzást a tér és az idő geometriai szerkezetének gyűrődéseként, görbületeként fogja fel. A görbületet a Föld, a Nap, a Galaktika és bármi más test energiája hozza létre. A gravitációs hullámok gyorsan változó hepehupák a téridő görbültségében, amelyek a fény sebességével terjednek.
A geometria “gyűrődését” egyszerűen jellemezhetjük egy adott helyen: megadjuk az oda illeszkedő kör sugarát. Szerencsére a legtöbb csillagászati tartományban a gravitációs hullámok hosszúsága sokkal kisebb, mint a többi fajta térgörbület sugara. Így eléggé pontosan fel tudjuk bontani a görbületet a háttérgörbületre és a hullámopk okozta görbületre. A háttérgörbület a görbület átlaga több hullámhossznyi távolságra. A hullámok görbülete a teljes görbület és a háttérgörbület különbsége.
Hogyan mérhetők a gravitációs hullámok? Az általános relativitáselmélet szerint a téridő görbületét az általa szomszédos részecskékben keltett viszonylagos gyorsulás útján mérjük. Egy elhanyagolható tömegű, a téridőt alig görbítő megfigyelő egy hozzá közeli részecskére ható erőt méri. Megteheti, hogy elfelejti a részecskét és méri a szabadesés gyorsulását. Az erőt úgy kapja, hogy a gyorsulást megszorozza a részecske tömegével. Más módon is mérhet: a részecskét egy önmagához képest rögzített pontban tartja, mérve az ehhez szükséges erőt.
Ha leszámítjuk a megfigyelő és a részecske esetleges együttes gyorsulásából származó erőt, akkor a keltett erő arányos a megfigyelő és a részecske távolságával. A részecskének a megfigyelőhöz viszonyított gyorsulását a téridő görbültsége idézi elő. Ezt az erőt bontja fel lassan változó (háttér) összetevőre és gyorsan változóra. Meggyőződik arról, hogy a közvetlen környezetében nincsenek gyorsan mozgó vagy változó tömegek. Ekkor a gyorsan változó összetevőt a gravitációs hullámoknak tulajdoníthatja.
Ha a gravitáció csupán hullámok alakjában van jelen, akkor a próbarészecske kicsiny, periodikus helyzetváltozást mutat.
Gravitációs hullámok keltése
Einstein már 1916-ban levezette a gravitációs sugárzás alapformuláját, amely ma is kitűnően megállja a helyét. Ez –a híres kvadrupólformula –a mozgó tömeg nyomatékának változásából származtatja a gravitációs teljesítményt. A hullámoknak és forrásaiknak a szerkezetét a multipólus-nyomatékok jellemzik. Például a pontszerű elektromos töltés körül gömbszimmetrikus mező alakul ki, amelynek a távolságfüggése is jellegzetes. Ez az “egypólus” mezeje. A mágnesrúd mezeje már irányfüggést is mutat. Ez a “dipólusmező”. A “kavdrupól” elnevezés az általános relativitáselméletnek arra az egyedülálló sajátságára utal, a tömegnyomatékok közül sem az egypólus, sem pedig a dipólus nem kelt hullámokat. A legalacsonyabb nyomaték a kvadrupólustag. (A teljesítmény e nyomaték harmadik időderiváltjának négyzetével arányos.)
A kvadrupólformula az általános relativitáselmélet gravitációs egyenleteiből következik. Eredetileg Einstein a levezetés során feltette, hogy a keltett gravitációs tér gyenge, és hogy a keltő anyag a fény sebességéhez képest lassan mozog. A kvadrupólformula azonban minden olyan forrásra használható, amelynek hosszúsága kisebb, mint a kibocsátott gravitációs hullámok hosssza.
A világmindenségből érkező gravitációs hullámok háromféle lefolyásúak lehetnek. Az egymás körül szoros pályán keringő kettős csilalgok gravitációs sugárzása hosszú ideig közelítőleg állandó rezgésszámú marad; a gravitációs sugárzása periodikus. E kettős rendszerek pályafutásuk végén, az elvesztett energia következtében egymásba zuhannak. Ekkor egyetlen rövid, nagy intenzitású impulzust sugároznak ki, amelynek a rezgésszáma gyorsan változik. Az ilyen típusú jeleket “kitörésnek” nevezik. Ilyen a felrobbanó szupernóvák gravitációs jelalakja is. A harmadik típusba a véletlenszerű gravitációs hullámok tartoznak. Ezeket például a világmindenség keletkezése után lezajló heves anyagmozgások keltik. Az észlelésük elvezethet a kozmológiai folyamatok jobb megértéséhez.
Az épülő gravitációs obszervatóriuok képesek lesznek mindhárom fajta gravitációs jel észlelésére.
A pulzárok szerepe
Laboratóriumi viszonyok között nem lehet kimutatható erősségű gravitációs hullámokat kelteni. Az asztrofizikai folyamatokban viszont az ott előforduló hatalmas anyagsűrűségek és a tekintélyes sebességek miatt a keletkező gravitációs hullámok mérhetőek. Ebből szemponból is igen nagy jelentőségű volt a pulzárok felfedezése. Az első négy pulzárt 1967-ben találta A. Hewish és Jocelyn Bell Cambridge-ben. Ma mintegy 450 pulzárt ismerünk. Egyedileg jellemző rádiójelalakjuk van, amelyek periódusideje a másodperc törtrészétől kb. négy másodpercig terjed. Körülbelül tucatnyi milliszekundumos (ezredmásodperc periódusidejű) pulzárt is ismerünk.
A pulzárok neutroncsillagok, kicsiny, 10–20 km átmérőjű égitestek, tömegük körülbelül 1,5 naptömeg: óriási a sűrűségük. A világítótoronyéhoz hasonló csóvában kibocsátott rádiójeleik a mozgásukról, belső szerkezetük átrendeződéséről is felvilágosítást adnak.
A PSR 1913+16 jelzésű kettős pulzárt 1974 nyarán vette észre először J. R. Taylor és doktorandusza, R. A. Hulse az arecibói (Puerto Rico) rádiótávcső segítségével. Kiderült, hogy a PSR 1913 + 16 rövid, 59 ezredmásodperces periódusideje 7,75 óránként visszatérő ingadozást mutat. Ez a nagy másodlagos periódus a keringésből származó Doppler-eltolódásra jellemző. A görbe alakjából kitűnik, hogy a pulzár pályája elipszis, amelynek a síkjára ferdén látunk rá. A látható tartományban a pulzár irányából semmit sem észlelünk: valószínű, hogy nemcsak a pulzár, hanem a társa is neutroncsillag.
A Földhöz legközelebbi pontból körülbelül 3 másodperccel hamarabb érkeznek a jelek, mint a legtávolabbiból. Ennyi időt vesz igénybe, hogy a fény áthaladjon a teljes pályán. Így megtudjuk, hogy a pálya kb. 1,4 millió km átmérőjű.
Kezdettől fogva az általános relativitáselmélet érzékeny kísérleti eszközét látták ebben a pulzárban, mert a két nagy sűrűségű égitest nagy sebességgel (a fénysebesség néhány ezrelékével) kering egymás erős gravitációs terében. Az általános relativitáselmélet egyik következménye, hogy a keringés ellipszise lassan elfordul a mozgás irányában, a pálya tehát nem zárt görbe. Ez a relativitáselmélet három klasszikus kísérleti bizonyítékának egyike, amelyet elsőként a Merkur bolygó keringésében mutattak ki. A mért szögértéke a Merkurénak sokszorosa, 4,2 fok/év.
A kvadrupólformulából a pályaadatok alapján meghatározható a gravitációs hullámok kisugárzására fordított teljesítmény. Ez a kereken 1025 watt teljesítmény a pálya menti mozgás energiáját csökkenti. Ezért az ellipszis nagytengelye (1,4 millió km) keringésenként 3,1 milliméterrel rövidül, ami 67 nsec periódusidő-csökkenésnek felel meg.
Taylor 12 éven át észlelte a kettős pulzár pályaadatainak változásait. Megállapította a keringési idő csökkenését. A pályaadatok mérése alapján meghatározott energiaveszteség 1% pontossággal megegyezik az általános relativitáselmélet jóslatával. Az elmélet és mérés e nagyszerű összhangját a gravitációs sugárzás létezésének erős bizonyítékaként értelmezik.
Az általános relativitáselmélet szerint a kettő rendszerek nem keringenek örökkön-örökké égi pályájukon. Ezzel fizetik meg a kisugárzott gravitációs teljesítmény számláját. Az adatok alapján a kettős pulzár sorsa is meghatározható. A pálya elnyújtsága csökken, és 250 millió év múlva gyakorlatilag körpályává válik, átmérője a Napéval lesz azonos. További százmillió év múlva a két égitest már 250 km-re megközelíti egymást. A folyamat ekkor már jelentősen felgyorsul, hiszen a teljes energia egyre nagyobb hányada fordul át a gravitációs sugárzás energiájává. Ez gyorsabb pályaméret- és keringési időcsökkenéssel jár együtt.
Lézeres észlelések
A hullámok kozmikus forrásai (kettős csillagok, szupernóva stb.) hatalmas teljesítményt sugároznak ki, de a nagy távolság miatt a hatásuk a Földön csekély. A gravitációs hullámok erősségét az általuk okozott viszonylagos megnyúlással jellemezhetjük. Ha az antenna hossza L és a gravitációs hullámok hatására dL hosszúsággal megnyúlik, akkor a viszonylagos megnyúlás: h = dL/L. Egy szupernóva-robbanás a Tejútrendszerben körülbelül h » 10-18 erősségű gravitációs hullámot küldene a Földre. Azonban átlagosan csak 40 évente várható ilyen esemény. A hozzánk közeli Szűz halmaz több ezer, a mi Tejútunkhoz hasonló galaktikát tartalmaz, így a várható eseménysűrűség is nagyobb. A legborúlátóbb becslések évi 3-4 eseményt jósolnak. A nagyobb távolság miatt azonban a gravitációs hullámok ezerszer gyengébbek, mint a Tejútról érkezőek. A LIGO és a VIRGO gravitációs detektorainak ezért kb. 10-21 relatív távolságváltozást kell kimutatniuk. Ilyen kis változások mérésére a már eddig is jól bevált Michelson-interferométert lehet használni (1. ábra). Egy nagy teljesítményű és igen pontosan stabilizált lézer fényét az osztótükör két ágra ontja. Ezek a karvégek tükreiről visszaverődve egyesülnek ismét az osztótükrön. Az eredményt fénydetektor észleli. A két ág úthosszát úgy állítják be, hogy az osztótükrön történő egyesülés ellentétes hullámfázisban történjék, és a fénysugarak pontosan kioltsák egymást. Így a detektorr a nem esik fény. Ha viszont gravitációs hullámok haladnak keresztül a karokon, akkor a karhosszak megváltozása miatt elromlik a kioltás, a detektor a gravitációs hullámok erősségével arányos fényintenzitást regisztrál. A gyakorlatban a fénysugár többször is visszaverődik egy karban, minden alkalommal a tükör más helyén. Ezáltal megsokszorozódik a fáziskülönbség.
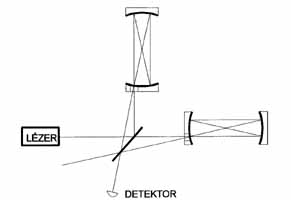
1. ábra. A fény útja a lézer-interferométerben
A mérési elv tehát egyszerű, megvalósíthatóságát már a hetvenes évek végén bebizonyította a kaliforniai Hughes Laboratóriumban épült Malibu interferométer. Eldőlt, hogy a lézeres interferometriát felhasználó mérési technika kellő érzékenységű detektorokat tud biztosítani a gravitációs hullámok kimutatására. A 80-as években sorra építettek a kutatóintézetek detektor-prototípusokat (München, Glasgow, Pisa, Caltech, MIT, Tokió, Perth). A detektorok érzékenysége folyamatosan javult. A 90-es évek elejére elérték a Tejútrendszer-beli szupernóvarobbanások gravitációs észleléséhez szükséges érzékenységszintet. Sajnos csak ekkor, így az 1987 februárjában a Nagy Magellán Ködben történt szupernóvarobbanásról még lemaradtak.
Az elért eredmények lehetővé tették az interferometrikus obszervatóriumok egy új nemzedékének a megépítését. A LIGO gravitációs obszervatórium két interferométer-rendszerből áll. az egyik egy Washington állambeli, korábbi nukleáris kísérleti telepen, a másik pedig a Luisiana állambeli Hanford támaszponton lesz. Legalább két interferométer szükséges ugyanis ahhoz, hogy a kozmikus eredetű jeleket megkülönböztessék a helyi zajoktól, kisebb-nagyobb földlökésektől. Mindegyik karhossz 4 km lesz, 1,2 méter átmérőjű csövekben halad a fénysugár, amelyekben igen nagy vákuum biztosítja a zajmentes terjedést. A végükben nagy visszaverőképességű tükör függ.
A LIGO rendszer megépüléséig a várható összkiadás 253 millió dollár, amelyből 210 milliót az Egyesült Államok kormánya ad, a többi pedig ipari támogatásból származik. Sok elvi műszaki probléma megoldása még hátra van. Nagy erőkkel folyik az e célra alkalmas nagy teljesítményű, igen stabil lézer fejlesztése, az interferométer tükreinek zajmentes felfüggesztését biztosító technika kialakítása, az adatfeldolgozás kifejlesztése.
A földi eredetű erőteljes háttérzaj – mely az alapzat rezgéseiből, a berendezés részeinek hőmozgásából, a lézerfény ingadozásaiból és egyéb forrásokból származik – rátelepszik a megfigyelésekre. Számítógép segítségével lehet a jelent megtisztítani. Ehhez azonban elengedhetetlenül szükséges, hogy a kiválasztandó jelalakot ismerjük. Ezt sablonnak nevezik. Elméleti fizikusok világszerte dolgoznak ezeknek a sablonoknak a kiszámításán. Csoportunk – Gergely Á. László, Perjés Zoltán és Vasúth Mátyás – például a forgó fekete lyuk köré befogott kozmikus test sugárzását tanulmányozza. Az ilyen testekből összegyűjtött anyaggyűrű mind a folyamatos, mind pedig a kitörésszerű gravitációs hullámoknak egyik fontos forrása.
Az
épülő nagyszabású LIGO és az európai VIRGO obszervatórium észlelései nyomán
hamarosan bepillantást nyerünk a neutroncsillagok és fekete lyukak titokzatos
világába, s várhatóan ismét alaposan átrajzolhatjuk majd a világmindenségről
kialakult képünket.