Hraskó Péter
Wigner Jenő kalandozásai a rezonanciák birodalmában

Van a fizikában három egymással nagyon szoros kapcsolatban álló formula, amelyeket Lorentz-görbének, a vonalszélesség képletének és Breit–Wigner-formulának hívnak. Nemcsak az a közös bennük, hogy alapvető fontosságúak: a matematikai alakjukat is ugyanaz az

képlet írja le (a, b és c pozitív konstansok, amelyek a három esetben különbözők). Ugyanarról a valamiről van-e szó három különböző összefüggésben, vagy lényegesen különböző tartalmakat kifejező matematikai képletek véletlen formai egybeeséséről? Ennek a némileg teológiai színezetű problémának a tisztázásában kiemelkedő szerepet játszott Wigner Jenő, aki egyébként nemcsak a Breit–Wigner-formula egyik felfedezője, hanem a vonalszélesség képletéé is.

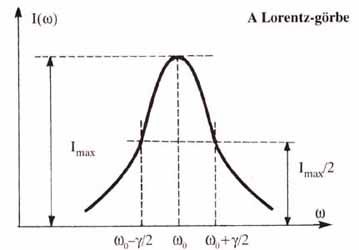
A Lorentz-görbe

H. A. Lorentz a fénytörés tanulmányozása kapcsán jutott el nevezetes formulájához. Az üvegprizma a szivárvány színeire bontja fel a ráeső napfényt. Így jön létre a színkép – vagy spektrum –, amely könnyen megmagyarázható a fény hullámelmélete alapján. Azt kell csupán feltenni, hogy az n törésmutató függ a fény w körfrekvenciájától és a frekvencia növekedésével nő. A törésmutatónak ezt a tulajdonságát hívják diszperziónak, az n(w) függvényt pedig diszperziós görbének.

A XIX. század második felében a diszperziós görbét abból a hipotézisből vezették le, hogy az anyag – a prizma üvegje – a fényben terjedő elektromos mező hatására polarizálódik, mert ellentétes töltésű részecskéket tartalmaz. Ezekre a hipotetikus töltött részecskékre már azelőtt használták az “elektron” elnevezést, mielőtt J. J. Thomson 1897-ben a katódsugarakban felfedezte a ma elektronként ismert elemi részecskét. Lorentz 1892-ben publikált elméletében az anyag pozitív és negatív töltésű részecskéi (“elektronjai”) rugalmas erővel vannak összekötve és valamilyen meghatározott w₀ frekvenciával képesek szabadon rezegni egymáshoz képest. A környező anyaggal való kölcsönhatás és az elektromágneses kisugárzás következtében azonban ez a szabad rezgés valójában folyamatosan fékeződik (csillapított rezgés), és ha nem hat valamilyen gerjesztő erő, hamar megszűnik.

A prizmára ráeső fényhullámban terjedő elektromos mező Coulomb-erővel hat a töltött részecskékre, amelynek következtében az ellentétesen töltött anyagrészecskék a fényhullám w körfrekvenciájával rezegni kezdenek egymáshoz képest. A periodikus erővel gerjesztett súrlódó harmonikus oszcillátor mozgásának a tárgyalása a mechanika viszonylag egyszerű feladatai közé tartozik. A gerjesztőerő folyamatosan növeli, a csillapítóerő pedig folyamatosan csökkenti a rezgés energiáját, amelyet egyéb energiafajtává, hővé és elektromágneses sugárzássá alakít át. Azt az energiát, amelyet az oszcillátor a csillapítás következtében az w körfrekvencia körüli egységnyi frekvenciatartományban egységnyi idő alatt valamilyen formában lead (és ugyanakkor a fényhullámból felvesz), az

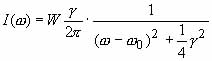
képlet írja le, amelyben g a súrlódási együttható és a rezgő tömeg szorzata, W pedig az időegység alatt leadott (és egyidejűleg felvett) összenergia (az I(w) integrálja). Az I(w) függvény a Lorentz-görbe. Matematikai szempontból ez ugyanaz a függvény, mint f(x), ha x-et w-val helyettesítjük és a konstansokat megfelelően választjuk meg. A függvény alakja nagyon egyszerű: egyetlen szimmetrikus csúcs a vízszintes tengely w₀ (azaz b) pontjában. A g a csúcs szélességét jellemzi: a görbe az w= w₀  ą g /2 pontokban csökken a csúcsban felvett maximális érték felére. A függvényt rezonanciagörbének is nevezik, mert azt fejezi ki, hogy a gerjesztőerő akkor ad át maximális energiát a rezgésnek és ezen keresztül az oszcillátor környezetének, amikor w körfrekvenciája közel van az oszcillátor szabad rezgéseinek w₀ körfrekvenciájához (rezonanciában van vele).
Lorentz elsődleges célja nem ennek, hanem az n(w) diszperziós görbének a meghatározása volt. Elektronelmélete segítségével ezt is kiszámította. Azt találta, hogy ha minden anyagfajtában több különböző w₀ körfrekvenciájú oszcillátor létezik, amelyeknek a frekvenciáját az egyes anyagokra tapasztalatilag kell meghatározni, akkor az olyan frekvenciákon, amelyek egyik ilyen karakterisztikus frekvenciához sincsenek közel, n(w) a frekvenciának valóban növekvő függvénye, ahogy a kísérletekből is megállapítható. Ilyen esetben a fénytörés úgy következik be, hogy a fénysugár gyakorlatilag nem veszít az energiájából, hiszen egyik oszcillátorral sincs rezonanciában.

A karakterisztikus frekvenciák közvetlen közelében azonban más a helyzet. Az n(w) függvény itt a frekvencia növekedésével csökken (anomális diszperzió) és a prizmában a fényenergia jelentős rezonáns elnyelődése következik be. Ezeket a frekvenciasávokat abszorpciós sávoknak nevezik.

Amikor a fény nem üvegen, hanem valamilyen ritka gázon halad keresztül, az abszorpciós sávok rendkívül keskeny abszorpciós vonalakká szűkülnek össze. Lorentz elmélete számot ad erről a jelenségről is. Ritka gázokban a fényhullám az egyes atomokat vagy molekulákat polarizálja, amelyek átlagban nagy távolságra vannak egymástól. Ennek az a következménye, hogy a gerjesztési energiájuk sokkal nehezebben adódik át a környezetnek, mint az üvegben, ahol a molekulák sűrűn helyezkednek el egymás mellett, és gyakorlatilag egyedül elektromágneses sugárzás formájában távozik. Lorentz elméletében ez a körülmény a fényenergia elnyelődését meghatározó paraméter csökkenésében, vagyis a rezonanciagörbe csúcsának a keskenyedésében jelentkezik (természetes vonalszélesség).

A vonalszélesség képlete

A spektroszkópiai módszerek finomodása lehetővé tette az abszorpciós vonalak alakjának a felbontását, és igazolta, hogy rájuk is érvényes az I(w) képlet. De a XX. század tízes, húszas éveiben ez már sokkal inkább problémát jelentett, mint magyarázatot. Időközben létrejött ugyanis a kvantumelmélet, amely Lorentz elmélete alól tökéletesen kihúzta a talajt. Fényesen beigazolódott ugyan, hogy az anyag legkisebb részecskéi – az atomok és a molekulák – elektromosan polarizálhatók, a karakterisztikus frekvenciákról pedig kiderült, hogy az energiaszintek közötti átmenetekhez tartozó Bohr-frekvenciákkal azonosak, amelyek a kvantumelmélet alapján ki is számíthatók. A Newton-egyenletet azonban, amelyen Lorentz számításai alapultak, felváltotta a Schrödinger-egyenlet, és hiába maradt a fizikai kép lényegében változatlan, egyáltalán nem volt nyilvánvaló, hogy a kvantumelméletből ugyanaz az I(w) rezonanciagörbe vezethető le, mint a klasszikusból.

A problémát Wigner Jenő és V. Weisskopf tisztázta 1930-ban két fundamentális dolgozatban, amelyek máig sem veszítettek a jelentőségükbő1. Wigner ekkor 28 éves volt, Weisskopf 22. A kvantumelmélet mindössze ötéves múltra tekintett vissza (Heisenberg mátrixmechanikája 1925-ben, Schrödinger hullámmechanikája 1926-ban keletkezett), ezek a fiatalemberek mégis virtuóz módon alkalmazták ezt a nehéz, új elméletet a spektrumvonalak alakjának vizsgálatára.

Akkor már lehetett tudni, hogy a fotonkibocsátással járó “kvantumugrás” az atom valamelyik gerjesztett állapotából az alapállapotba (vagy egy alacsonyabb energiájú gerjesztett állapotba) a radioaktív bomláshoz hasonló jelenség, amely az exponenciális bomlási törvényt követi. Einstein még 1916-ban ennek a fizikai képnek az alapján származtatta le a fekete sugárzás spektrumát. Az exponenciális bomlási törvényben szereplő bomlási állandó értékére 1927-ben vezetett le képletet Dirac a kvantumelmélet alapján. Wigner és Weisskopf elgondolása szerint az izoláltnak tekinthető atomok esetében ez a radioaktív bomlási folyamat felel meg az oszcillátorok csillapodását okozó súrlódásnak Lorentz elméletében, következésképpen a Dirac által kiszámított bomlási állandónak kell betöltenie a g állandó szerepét a spektrumvonal alakját leíró I(w)-képletben.
Ahhoz, hogy ezt az elgondolást pontosan megfogalmazhassák, Wignernek és Weisskopfnak új matematikai eljárást kellett kifejlesztenie, amelyet ma Wigner–Weisskopf-perturbációszámításnak nevezünk. A perturbációs módszer közelítő eljárás, amelyet akkor lehet alkalmazni, amikor valamilyen gyenge hatás következményét kell figyelembe venni. A gerjesztett állapotú atom elektromágneses sugárzását előidéző hatás gyenge a Coulomb-erőhöz képest, amely az atomon belül az elektronok és az atommag között hat. Ezért tudta Dirac kiszámítani ugyancsak perturbációs eljárással a fotonemisszió bomlási állandóját.

A bomlási állandó kiszámításához azonban elég összehasonlítani az atom állapotát két egymáshoz infinitezimálisan közeli időpillanatban. Ezt a mennyiséget ugyanis az határozza meg, hogy tetszőlegesen rövid dt idő alatt a gerjesztett atomok mekkora hányada ugrik át fotonemisszióval alacsonyabb energiájú állapotba. Ahhoz azonban, hogy meg lehessen állapítani a bomlási állandó pontos helyét a spektrumban, olyan perturbációs módszer kell, amely hosszú időtartamokra is érvényes. Ez azzal a híradástechnikából is jól ismert ténnyel függ össze, hogy a spektrális (w-tól függő) mennyiségeket annál pontosabban lehet meghatározni, minél hosszabb ideig figyeljük meg a szóban forgó folyamatot.

A Wigner–Weisskopf-módszer olyan perturbatív eljárás, amely a bomlási idővel összemérhető időtartamokra is alkalmazható. A legfontosabb következtetések, amelyekre módszere segítségével a két kutató eljutott, a következőkben foglalhatók össze.

Jelöljük az atom kvantumállapotainak az energiáját az energia növekedésének sorrendjében E₀, E₁, E₂, ... -vel. E₀ az alapállapot, E₁ az első gerjesztett állapot energiája. Az alapállapot stabil, az első gerjesztett állapot pedig az e^–t/t exponenciális bomlási törvény szerint fotonkibocsátással az alapállapotra bomlik el (t az időállandó, 1/t pedig a bomlási állandó).

Legyen w₁₀ annak valószínűsége, hogy miközben az atom az első gerjesztett állapotából az alapállapotba “ugrik át”, olyan fotont emittál, amelynek az energiája az E körüli egységnyi energiatartományba esik. Wigner és Weisskopf szerint ezt a valószínűséget az

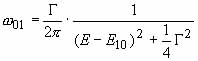
képlet határozza meg, amelyben E₁₀ = E₁ – E₀ a bomló állapot gerjesztési energiája és G = 2/t. Tisztán matematikai szempontból ez függvény – a vonalszélesség képlete – pontosan ugyanolyan, mint a Lorentz-görbe. A görbe alakját meghatározó három konstans fizikai jelentése azonban a két esetben lényegesen különböző. A független változó sem ugyanaz, bár az E = w képlet szoros összefüggést állapít meg a foton energiája és frekvenciája között. Ha az alapállapot és az első gerjesztett állapot energiája pontosan egyenlő lenne a kvantumelméletből kiszámítható E₀, E₁ energiával, akkor az energiamegmaradás törvénye szerint a foton energiájának pontosan E10-val kellene egyenlőnek lennie, márpedig Wigner és Weisskopf fenti képlete szerint ez az energia szór az E₁₀ érték körül. A Wigner–Weisskopf-elmélet eszerint azt igazolja, hogy a gerjesztett állapot energiája nem egyenlő pontosan E₁-gyel, hanem van valamilyen DE bizonytalansága, amelyet a G vonalszélesség határoz meg. Ha DE-n azt az eltérést értjük E₁₀-tól, amelynél a w₁₀ (E) függvény a maximumáról a felére csökken, akkor nyilván DE = G/2. Mivel azonban G 2/t-val egyenlő, ezt az egyenlőséget

DE ˇ t = 

alakban is felírhatjuk: minél rövidebb élettartamú a bomló kvantumállapot, annál pontatlanabbul van meghatározva az energiája. Mivel az alapállapot stabil, az E₀ energiának nincs bizonytalansága.

Emlékezzünk most vissza Lorentz elméletére, amelyben ugyanaz az I(w) képlet írja le az oszcillátorok által leadott és felvett energiát. A vonalszélesség képlete is ilyen kettős arculatú. Ha az w frekvenciájú fény ritka gázon halad keresztül, amelynek atomjai túlnyomórészt alapállapotban vannak, akkor gerjeszti számottevő mértékben az atomokat az első gerjesztett állapotra, amikor az E = w fotonenergia rezonál a gerjesztési energiával (w ť E₁₀). A gázon áthaladó fehér fényből ezek a frekvenciák fognak hiányozni. A helyükön megjelennek a keskeny abszorpciós vonalak, amelyeknek az alakját szintén a vonalszélesség képlete írja le.

A Wigner–Weisskopf-módszer a megszületése óta eltelt 70 év során a legkülönbözőbb fizikai jelenségek tárgyalásánál bizonyult nélkülözhetetlennek. A 60-as években például az időtükrözési szimmetriának a semleges K-mezonok bomlásában tapasztalható sérülését ezzel az eljárással lehetett matematikailag analizálni.

A Breit–Wigner-formula

Az atomfizikáról most át kell váltanunk a magfizikára, mert a Breit–Wigner-formula – a fizika egyik legtöbbet használt összefüggése – annak a robbanásszerű fejlődésnek volt a következménye, amely a magfizikában a 30-as évek közepén következett be. 1935-re világossá vált, hogy amikor lassú, néhány elektronvolt energiájú neutronnyalábbal bombáznak nehéz atommagokat, rezonanciaszerű kölcsönhatás jön létre a neutronok és az atommagok között. A kölcsönhatás erősségét a hatáskeresztmetszetnek nevezett mennyiséggel mérik, amelyet s-val jelölnek. A s négyzetméter dimenziójú mennyiség és az atommag geometriai keresztmetszetével lenne egyenlő, ha a neutron pontszerű volna, és csak akkor lépne kölcsönhatásba az atommaggal, amikor eltalálja. A valóságos hatáskeresztmetszet azonban a szóródási folyamat kvantumos természete következtében nagyságrendekkel is meghaladhatja az atommag geometriai keresztmetszetét. Ez történik az említett rezonanciáknál: a s(E) görbe, amely a hatáskeresztmetszet függését írja le a neutronok E energiájától, egymástól többé-kevésbé elkülönülő rezonanciacsúcsokat mutat.

A tapasztalat szerint a rezonanciacsúcsok tartományába eső energiákon a neutronnal két dolog történhet: vagy szóródik az atommagon, vagy befogódik, és az új, eggyel több neutront tartalmazó izotóp elektromágneses úton – g-sugárzással – veszíti el az energiáját. Az első folyamat hatáskeresztmetszetét ss(E)-vel, a másodikét sg(E)-vel fogjuk jelölni. Breit és Wigner 1936-ban publikált elmélete ezekre a görbékre a

képleteket szolgáltatja, amelyekben E a rezonanciaenergia, l pedig a neutron de Broglie-hullámhossza. A hatáskeresztmetszet maximuma az E energiánál van, a csúcs szélességét pedig a G értéke határozza meg, amely a szóródási és a befogási folyamatra ugyanaz. A Gs, Gg mennyiségeket parciális szélességeknek nevezzük. Az összegük G-val egyenlő, a G_s /G és a G_g/ G hányadosok pedig a szóródás és a befogódás részarányát határozzák meg.

Wigner és négy évvel idősebb kollégája, G. Breit teljesítményét csak akkor értékelhetjük méltóképpen, ha legalább futólag felidézzük az atmoszférát, amelyben ez az eredmény megszületett. Nem ők voltak az elsők, akik a lassú neutronokkal végbemenő folyamatok hatáskeresztmetszetét rezonanciaformulával próbálták leírni. Ilyen elméletet 1935-ben többen is közöltek, egyebek között H. Bethe és E. Fermi, mindketten jövendő Nobel-díjasok. A neutronok szóródását a nehéz atommagokon ők ahhoz hasonlóan képzelték el, ahogy a fény szóródik egy olyan mikroszkopikus üvegszemcsén, amely összemérhető a fény hullámhosszával. A neutron befogódásának ebben az elképzelésben a fény részleges abszorpciója felelt meg, amely amiatt következik be, hogy az üveg nem tökéletesen áttetsző. Ez a modell a hatáskeresztmetszetekre szintén rezonanciaformulát eredményez, és ennyiben helyesen tükrözi a tapasztalatot, de a szórási és a befogási folyamatok viszonylagos súlyára hibás eredményt ad. Bethe és Fermi számításai szerint a neutronok befogódását mindig jelentős szórásnak kell kísérnie, de ezt a mérések egyértelműen cáfolták: a befogás bizonyult domináns folyamatnak, amely nagyságrendekkel volt intenzívebb, mint a szórás.

1935 végére ez a probléma vált a magfizika központi kérdésévé. A felfokozott figyelmet, amelyben részesült, világosan mutatja, hogy a megoldást csaknem napra egyszerre találta meg Breit és Wigner, valamint Niels Bohr. Az új elgondolás lényege az volt, hogy a rezonanciák annak az atommagnak a kvantumállapotai, amely a neutron befogódásakor jön létre. Az atomok gerjesztett állapotaival állíthatók párhuzamba, amelyek fotonelnyeléssel jönnek létre az alapállapotból, bár a részletek tekintetében a két eset között fontos eltérések lehetségesek.
A Gszélesség most is a rezonanciaállapot bomlási állandójával arányos mennyiség, és mivel ez az állapot egyaránt elbomolhat neutronkibocsátással (szórási folyamat) vagy gamma-sugárzással (befogás), ezért mindkét folyamat hozzájárul a bomlási állandóhoz. Ezt fejezi ki a G = G_s + G_g képlet, amelyre fentebb már utaltunk. Mivel a tapasztalat szerint a befogás a szórásnál sokkal intenzívebb folyamat, G_sŤ G_g és a rezonanciák megfigyelt szélessége praktikusan a befogási folyamat szélességével egyenlő. Bethe és Fermi elméletében ezzel szemben a rezonanciák szélességét egyedül a szóródás határozta meg, rezonanciaformulájuk nevezőjében ugyanis a G helyén G_s állt, ezért jósolt az elméletük a valóságosnál intenzívebb neutronszórást.

Bohr 1936. január 27-én a Koppenhágai Akadémia felolvasóülésén ismertette a magfizikai rezonanciákra vonatkozó elképzelését. Az előadás szövege a Nature február 29-i számában jelent meg. Bohr február 11-én Londonban is tartott ugyanerről előadást. A folyóirat szerkesztősége annyira fontosnak tartotta a kérdést, hogy ugyanabban a február 29-i számban a News and Views rovat külön is beszámolt erről az előadásról. Breit és Wigner cikkét február 15-én vette kézhez a Physical Review szerkesztője, és a folyóirat április l-jei számában jelent meg.

Bohr és a Breit–Wigner páros gyökeresen eltérő módon tárta a fizikus közvélemény elé a neutronrezonancia-rejtély megoldását. Bohr cikke színtiszta szöveg, egyetlen képlet sincs benne, és kifejezetten olvasmányos. Breit és Wigner dolgozata tele van formulákkal, amelyeknek a levezetését nem könnyű követni. Bohr szemléletes magyarázatot ad arra, miért nyomja el a befogás a szórási folyamatot. A neutron úgy kezd kölcsönhatni a maggal, hogy ütközik annak valamelyik nukleonjával. Eközben az energiája csaknem mindig a kötési energia értéke alá csökken, ennek következtében kötve marad az új izotópban, és létrejön a közbenső vagy kompaund mag. Csak nagyon hosszú idő múlva következik be az, hogy a közbenső mag energiája újra egy neutronon összpontosuljon, amely azután a magból kirepülve szórási folyamatot idéz elő. A közbenső mag sokkal gyakrabban veszítheti el a gerjesztési energiáját g -kvantum kibocsátásával, ezért sokkal nagyobb a befogás valószínűsége, mint a szórásé.

Breit és Wigner tárgyalása kémiai analógián alapult. Wigner és berlini tanára, Polányi Mihály még 1925-ben publikált egy dolgozatot arról, hogy a kémiai reakciók során két reagáló atom kölcsönhatásában néha rezonanciaszerű maximum figyelhető meg, és ez annak következménye, hogy a két atom viszonylag hosszú élettartamú közbenső molekulát képez. A hatáskeresztmetszet-formulákat azonban nem lehetett egyedül ennek a fizikai képnek az alapján “kapásból” felírni. Breit és Wigner ugyanannak a hosszú időtartamokra érvényes perturbációszámításnak a segítségével származtatta őket, amelyet hat évvel korábban Wigner az atomi nívók bomlási spektrumának a tárgyalására dolgozott ki Weisskopffal közösen. Pedig pontosan tudták, hogy ennek a módszernek az alkalmazhatósága az adott esetben legalábbis kétséges – a cikkben ezt külön hangsúlyozták. A magerők ugyanis sokkal intenzívebbek, mint az elektromágneses kölcsönhatások, nem tekinthetők “kis korrekciónak”, amit perturbációs módszerrel figyelembe lehet venni. Azonban bizonyára elég mélyen bele tudtak látni a problémába ahhoz, hogy bizonyosak lehessenek benne: képleteiket, amelyeket tökéletlen módszerrel kaptak, sokkal általánosabb feltételek mellett is le lehet vezetni, csak éppen az adott pillanatban még nem tudtak ennek a meggyőződésüknek világos matematikai megfogalmazást adni. Az elkövetkező két évtizedben Wigner egyéb jelentős munkái mellett kidolgozta a magreakciók általános elméletét, az R-mátrix-elméletet, amelynek keretében a Breit–Wigner-formulák perturbációs közelítés nélkül kaphatók meg. Ugyanerre a következtetésre a Wignerétől többé-kevésbé eltérő utakon mások is eljutottak. Kiderült, hogy a formulák érvényességéhez egyetlen speciális feltevés szükséges: az, hogy a kompaund magnak létezzenek az atomok gerjesztett állapotaihoz hasonló, viszonylag hosszú élettartamú kvantumállapotai. Ha ez teljesül, a képletek már nagyon általános fizikai elvek alapján levezethetők.

A magreakciók általános elméletén dolgozva Wigner a reakciók rengeteg különleges tulajdonságát fedte fel. Megállapította például, hogy amikor valamilyen energián átlépve lehetővé válik új végtermékek megjelenése (“megnyílik egy új csatorna”), a többi folyamat hatáskeresztmetszetében ún. küszöbeffektusok, hegyes csúcsok, mélyedések vagy lépcsők jönnek létre. Az ötvenes években az Annals of Mathematics hasábjain egy sor dolgozatban vizsgálta, milyen eloszlást mutatnak a nehéz atommagok rezonanciái a közöttük lévő távolság függvényében. Ezek a vizsgálatok arra a meglepő következtetésre vezettek, hogy a rezonanciák “taszítják egymást”. De ez már egy másik történet.