Róma; 1633: Galilei a Szent Inkvizíció elôtt:

...én mégis egy könyvet írtam és kinyomattam, amelyben a már elítélt doktrínát tárgyalom és igen nyomós érveket hoztam fel mellette anélkül, hogy választ adtam volna ezekre; és ezen okból a Szent Hivatal úgy találta, hogy erôsen gyanúsítható vagyok eretnekséggel – vagyis hogy azon a véleményen voltam és hittem, hogy a Nap a világ közepe és mozdulatlan, és a Föld nem a közép és mozog.

Ezért attól a kívánságtól vezérelve, hogy eloszlassam Eminenciáitok és minden hívô keresztény elméjében ezen ellenem okkal felmerült erôs gyanút, tiszta szívvel és nem tettetett hittel megtagadom, elátkozom és megvetem a fent mondott hibákat és eretnekségeket és általánosságban minden tévedést, tévelygést, bármit, ami a Szent Egyház ellen van.

És ezzel megszületik a Galilei-mítosz: Galilei neve ettôl kezdve összefonódik a begyepesedett doktrínák elleni, az igazságért vívott harccal. Még a huszadik században is a forradalmi haladó körök az ô nevét veszik fel. Einstein fogalmazza meg a mûvelt nagyközönség véleményét a Dialogo angol nyelvû kiadásának elôszavában.

És íme elôttünk áll egy ember, akinek szenvedélyes akarata, intelligenciája és bátorsága van ahhoz, hogy mint a józan gondolkodás képviselôje, szembeszálljon azok csapatával, akik a nép tudatlanságára és a papi és professzori köpenyben tanítók indolenciájára támaszkodva az elfoglalt hatalmi pozícióikat védelmezik. Rendkívüli írói adottsága lehetôvé teszi számára, hogy korának mûvelt embereihez olyan tisztán és meggyôzôen beszéljen, hogy ezzel a kortársak antropocentrikus és mitikus gondolkodását legyôzze, és ôket egy, a kozmosszal szembeni objektív és kauzális beállítottsághoz visszavezesse, amely beállítottság a görög kultúra virágzásával együtt letûnt az emberiség számára.

Itt meg kell szakítanunk az idézetet. Einstein ennyire magáévá tenné az általános véleményt? Nem jellemzô rá! De figyeljük csak a folytatást!

Amint ezt így kijelentem; rögtön látom is, hogy én is áldozatul esem mindazok szokásos gyengeségének, akik megittasulva mértéktelen vonzalmuktól, hôsük alakját túlméretezetten felnagyítják. Lehetséges ugyanis, hogy a sötét korok merev tekintélytiszlelete által megbénított lelkek a XVII. században már annyira magukhoz tértek, hogy egy túlélt, intellektuális tradíció kötelékei tartósan úgysem béklyózhatták volna le ôket akár Galileivel, akár Galilei nélkül.

Az elkövetkezendôkben ezen idézet szellemében egyrészt szetetnénk hangsúlyozni Galilei centrális szerepét a tudománytörténetben, másrészt megmutatni, hogy a kor már valóban megérett az új eszmék befogadására és továbbvitelére, akár Galilei nélkül is. Németh László drámájának legdrámaibb jelenetében – a Torricellivel folytatott beszélgetésben – Galilei maga is megéli ezt, természetesen személyes tragédiájaként.

A könyv, amelyikrôl az esküben is szó esik, az 1632-ben megjelent Dialogo, vagy teljes nevén Párbeszéd a két világrendszerrôl, a ptolemaioszi és a kopernikuszi rendszerrôl. Ebben a könyvben négy napon keresztül hárman beszélgetnek: egy Arisztotelész-hívô, ô védi a ptolemaioszi rendszert, amely szerint a mozdulatlan Föld a világ közepe, és körülötte keringenek a bolygók, sôt a Nap is; egy másik a kopernikuszi rendszer mellett érvel, hogy tehát a mozdulatlan Nap van középen, és a Föld egy a keringô hat bolygó közül, míg a harmadik egy józan, elfogulatlan vitapartner.

Ha az olvasó kezébe veszi a könyvet, az elsô meglepetés: a könyv nem latinul, a tudomány nyelvén, hanem olaszul íródott, olyan nyelvezettel, mint ahogy az emberek a társaságban, utcán, piacon beszélnek: világos fogalmak, minden gondolatmenet megérthetô, végigkövethetô – szinte szájba rágó. Természetesen fel kell dolgozni a több száz oldalt, hogy tisztán lássuk, mit is akar Galilei mondani. A könyv azt a látszatot kelti, hogy egyforma súlyú érvek hangzanak el az egyik, ill. a másik rendszer ellen és mellett, és az olvasóra van bízva, hogy melyiket fogadja el. A valósógban azonban – ezt természetesen a Szent Inkvizíció is helyesen látta meg – a valóságban a Dialogo egyértelmû kiállás a kopernikuszi rendszer mellett.

Ha Galilei semmi mást nem alkotott volna, mint ezt a csodálatos olasz prózában megírt tudományos és tudomány-népszerûsítô könyvet, már akkor beírta volna nevét a tudománytörténet legnagyobbjai közé. Nem csoda, hogy Galilei ezen mûve hatásában – elsôsorban filozófiai és társadalmi hatására gondolunk – túlszárnyalta minden egyéb mûvét, hozzá kell tenni, másokét is. A hatáshoz természetesen hozzájárult Galilei tragikus sorsa, a kialakuló Galilei-mítosz és így Galilei neve lassan a formálódó modern tudomány szinonímája lett: modern természettudomány = Galilei, ez volt az egyszerû és – ez sokszor döntô fontosságú – könnyen memorizálható képlet.

Amint azonban a 20. századi modern tudománytörténészek "megszállták" az 1600 körüli kort és részletesen kezdték kutatni, megindult Galilei esetében egy deheroizálási folyamat. A tudománytörténészek ugyanis rájöttek arra, hogy egy sor Galileinek tulajdonított eredmény sokkal korábbi, így a modern tudomány kezdetét vissza kellett korábbra helyezni; elôször csak 1–2 évszázaddal – Leonardóig –, de miután kiderült, hogy a "sötét középkorban" milyen értékes gondolatok születtek, akár 3 évszázaddal is korábbra. A tudománytörténészek szerint a Galilei-mítosz káros volt olyan szempontból, hogy fényével túlragyogott és ezzel árnyékba borított sok értékes személyt és értékes ismeretet, amely egyébként közkincs lehetett volna.

Végül is a heroizálás és deheroizálás kölcsönhatásából egy tisztultabb Galilei-kép állt össze. Abban minden tudománytörténész egyetért, hogy Galileinek centrális szerepe van a modern tudomány és világnézet kialakításában, csak az nem világos, hogy mibôl áll ez a szerep, és melyek Galilei legjelentôsebb felfedezései, megállapításai. Arthur Koestler, a tôle megszokott sokkoló módon például ezt állítja:

Ellentétben még a legújabb tudománytörténeti könyvek megállapításával Galilei nem találta fel a teleszkópot, sem a mikroszkópot, sem a hômérôt, sem az ingaórát. Nem fedezte fel az inerciatörvényt, még kevésbé az erô vagy sebesség paralelogrammáit, sem a napfoltokat. Nem járult hozzá semmivel az elméleti asztronómiához. Nem dobott le köveket a pisai ferde toronyból és nem bizonyította be a kopernikuszi rendszer igazságát. Nem kínozta meg az inkvizíció, nem sínylôdött annak kazamatáiban és sohasem mondta: eppur si muove. És végül nem volt a tudomány mártírja.

Ezzel szemben ô tekinthetô a modern dinamika megalapozójának...

Ha mi a magunk részérôl hozzátesszük, hogy Galileit nem tekintjük a dinamika megalapozójának, akkor mi marad Galilei számára? Nagyon sok. Íme:

1610-ben megjelenik a Sidereus Nuncius, a Csillaghírnök... Galilei – úgy tûnik – elôször fordította a távcsövet az ég felé, vagy legalábbis elôször írta le, hogy mi látható vele az égbolton. Azt általáhan elfelejtjük, hogy Kopernikusznak, Tycho de Brahénak még nem volt távcsöve. Galilei egy holland minta után készítette távcsövét, de amit meglátott vele, azok csodálatosan újak: a Jupiter körül holdak keringenek. Ennek a felfedezésének még elvi jelentôsége is volt: íme a kopernikuszi rendszer modellje az égbolton, de a pragmatikus Galilei gondolt ezen jelenség gyakorlati felhasználására is: a holdak táblázatba foglalt mozgástörvényén keresztül a nyílt óceánon a hajók navigációs segédeszköze lehetne. A Tejútról Galilei megállapítja, hogy az csillagok halmaza, a Vénuszról pedig, hogy ugyanolyan fázisai vannak, mint a Holdnak. Ezt a felfedezését Galilei egy anagrammában kódolta, amelynek megfejtése: Cynthiae figuras aemulatur mater amorum. Cynthia (vagyis a Hold) alakját utánozza a szerelem anyja, vagyis a Vénusz.

Egy fizikus számára a Galilei ezen könyvében szereplô eredmények közül talán a legcsodálatosabb a Hold hegyeivel kapcsolatos egyik állítása. Távcsövével jól látta a Hold hegyeit, krátereit, síkságait, de Galilei ezen túlmenôen azt is meg tudta állapítani, hogy milyen magasak ezek a hegyek. Kiindulópontja egy jelenség zseniális érielmezése. Észrevette, hogy félhold idején, amikor tehát a sötét és a megvilágított részeket egy átmérô választja el, az átmérô közelében a sötét részben néhány fénylô pont látható. Ezt nagyon helyesen úgy értelmezte, hogy ezek kiemelkedô hegycsúcsok, amelyeket a Nap még megvilágít, annak ellenére, hogy a Hold azon oldala már sötét. Azt könnyen meg tudta állapítani, hogy ezek a pontok milyen messze vannak a sötét és világos részeket elválasztó átmérôtôl – természetesen a Hold-átmérô hányadában kifejezve. Most már csak egy kis geometriai megfontolás, és kiadódik a hegy magassága, ismét csak a Hold-átmérô hányadában. De ez az átmérô már ismert volt, így a hegyek magasságát össze Iehetett hasonlítani az Appennini-hegyek magasságával. Galilei zsenialitása a jelenség helyes értelmezésében mutatkozik meg.

Galileinek a tudomány – tehát nem a filozófia vagy a világnézet – szempontjából legjelentôsebb mûve a per utáni házi ôrizetben írt és 1638-ban Leydenben megjelent mûve, a Discorsi (Beszélgetések két új tudományról). Ebben írja le a ma középiskolájában tanult jelenségeket, mint amilyen a lejtôn való mozgás, az inga mozgása vagy a ferde hajítás. Azt, hogy a ferdén hajított test parabolapályát ír le, Galilei még az elôszóban is külön kiemeli, mint az ô eredeti megállapítását. De sok egyéb témakör is szerepel: szilárdságtani problémák, vagy ami még fontosabb, a vákuummal kapcsolatos nézetei.

Galilei ezen érdemeit semmiféle bírálat nem homályosíthatja el. A most következô megállapításoknak is csak az a célja, hogy a kortársak és elôdök érdemét is a helyes megvilágításban lássuk.

Galilei sorsát még ma is sokan úgy látják, hogy a hivatalos tudomány, akár tudatlanságból, akár irigységbôl, féltékenységbôl elnyomja az újra törekvô haladó tudóst. Ez gyakran hivatkozási alapul szolgál arra, hogy humán beállítottságú "lelkes értelmiségiek" kiálljanak a meg nem értett, perifériára szorult tudósok, feltalálók mellett a hivatalos tudománnyal, a hivatásos tudósokkal szemben. Természetesen tisztáznunk kellene, hogy kik a hivatásos tudósok. De ha mi az alkotó, élen járó kortárs tudósokat nézzük, akkor, bármilyen megdöbbentônek hangzik, de meg kell állapítanunk, hogy Galilei néhány fontos területen el volt maradva az akkori tudományos élvonaltól.

Galilei 1632-ben még ragaszkodott az égitestek körpályán való mozgásához mint természetes mozgásformához, amikor Kepler 1619-ben a Világ harmóniája címû mûvében már megállapítja a bolygómozgás máig érvényes három törvényét, közöttük az ellipszispályán való mozgás törvényét, ugyanakkor a bevezetôben a kopernikuszi rendszerrôl ezt írja:

Mindenekelôtt az olvasónak tudomásul kell vennie, hogy ma már minden asztronómus számára teljesen nyilvánvaló, hogy az összes bolygó a Nap körül kering a Hold kivételével: egyedül az ô számára jelent a Föld középpontot.

A kopernikuszi rendszer igazságát (Kepler szerint) mint magától értetôdô tényt kell elfogadni, nem kell sok száz oldalon nagy ravaszsággal igazolni. Érdekességként még megemlítjük, hogy egy olyan ifjú titán, mint amilyen ebben az idôben Descartes volt, járt Itáliában, de semmi jele, hogy igyekezett volna Galileit felkeresni, hogy lerója nála tiszteletét; sôt azt írja Galilei könyvérôl: "Beleolvastam, úgy látom, jól filozofál, de azt is látom, hogy nem követi mindig a legrövidebb utat, és megállapításaihoz nem kell valami nagy geométernek lenni." Nem is olvasta végig Descartes a könyvet, mert unta.

Milyen ismeretek és tudások tûntek el Galilei ragyogó Iényének árnyékában?

Tanulságos lenne egy televíziós kulturális vetélkedôn föltenni a kérdést, hogy az alábbi két idézet melyik korból és kitôl való.

Íme az elsô idézet:

...Továbbá úgy vélem, hogy csak azt érzékelhetjük, hogy egyik test helyzete a másikhoz képest megváltozik. Ennek alátámasztására (a következô érvet hozhatjuk fel): ha egy ember egy hajón utazik – nevezzük ezt a hajót a-nak –, amely nagyon simán halad – egyébként akár gyorsan, akár lassan –, és ez az ember semmi mást nem lát, mint egy másik, b nevû hajót, amely minden tekintetben azonos módon halad, mint az a hajó, amelyben emberünk utazik, akkor én azt állítom, hogy ezen ember számára úgy tûnik, hogy egyik hajó sem mozog. És ha a nyugalomban van és b mozog, úgy jelenik meg és tûnik számára, hogy b mozog, viszont ha a mozog és b nyugszik, ez is úgy tûnik számára, mint elôbb, hogy a nyugalomban van és b mozog.

És a másik idézet:

... Mert számunkra világos, hogy ez a Föld valóban mozog, de mégsem tûnik mozgásnak, miután nem fogtuk fel a mozgást másképpen, mintha valamilyen rögzítettel hasonlítjuk össze. Ha egy ember a csónakban a folyó közepén nem tudja, hogy a víz folyik, és nem Iátja a partot, hogyan tudná észlelni azt, hogy a csónakja mozog? Ennek megfelelôen úgy fog látszani a megfigyelô számára, legyen a Földön, a Napon vagy akár egy másik csillagon, hogy ô a mozdulatlan középpontban van, és a többi dolgok azok, melyek mozognak.

Itt a Föld mozgása melletti érvek hangzanak el, és a vájt fülûek azt is észreveszik, hogy az érvelés a késôbbi Galilei-féle relativitás elvét használja, tehát az idôpont 1600 körüli év, a szerzô minden bizonnyal maga Galilei. Az idézetek valójában sokkal korábbiak: az egyik Nicole d'Oresme püspöktôl származik 1350 táján, tehát 300 évvel koráóbi... A másik Cusanustól való, a "bíboros és eretnek"-tôl, ahogy Vas István egyik versében nevezi, úgy 200 évvel Galilei elôtt vélekedett így.

Talán feltûnt, hogy eddig nem volt szó Galilei legismertebb kísérletérôl, a pisai ferde toronyban végzett ejtési kísérletérôl. Sokan úgy vélík, hogy a valóságban Galilei ezt sohasem végezte el, legálábbis ô maga nem ír róla. Viszont olvassuk el Stevin naplóját 1586-ból, tehát majdnem fél évszázaddal a Dialogo megjelenése elôtti idôbôl:

"Vegyünk két ólomgolyót (mint azt a felettébb tudós és a természet titkait legserényebben kutató Jan Cornets de Groot úr, valamint jómagam tettük), amely ólomgolyók közül az egyik tízszer nagyobb és súlyosabb, mint a másik, és ejtsük le ôket egyszerre 30 láb magasból egy deszkára vagy bármire, amin jól kivehetô hangot adnak. Azt fogjuk találni ... hogy annyira egyidejûleg esnek a deszkára, hogy a két hang egynek és ugyanannak tûnik. Úgy taIáljuk, hogy akkor is ez történik, ha két egyforma nagy golyóval kísérletezünk, amelyek súlya azonban úgy aránylik, mint egy a tízhez. "

Az már a tudomány szociológiájához, a sztárkultusz örök divatjához tartozik, hogy a társadalom nagyobb jelentôséget tulajdonít egy Galilei által (esetleg) el sem végzett, mint a Stevin által ténylegesen elvégzett kísérletnek.

A 17. század elsô évtizedeinek másik nagy egyénisége Kepler, Galilei kortársa, levelezô partnere. Ôt sokan a tudománytörténet egyik legizgalmasabb egyéniségének tartják. Vallásos, számmisztikával telített, csapongó fantáziájú, ugyanakkor a tényeket legmesszebbmenôen és legkritikusabban tisztelô és figyelembe vevô kutató. A természet törvényeihez vallásos áhítattal közeledik. A már említett könyvének, az 1619-ben megjelent, a Világ harmóniája címû könyvének bevezetôjében ezt írja:

Te, aki a természet fényével ébresztesz bennünk vágyat a kegyelem fénye iránt, hogy azzal a dicsôség fényébe vezess bennünket, hálát adok Neked, Teremtô Istenem, aki gyönyörködtem alkotásaidban és örvendeztem kezed mûvében. Íme most befejeztem munkámat, belefektetve elmém minden erejét, amellyel kegyes voltál ellátni; azok számára, akik fejtegetéseimet olvasni fogják, nyilvánvalóvá lesz a Te mûved dicsôsége, és végtelenségébôl annyi, amennyit elmém korlátoltsága felfoghatott.

Keplert természetesen elsôsorban a bolygók mozgására vonatkozó három törvényérôl ismerjük. De nevét viseli a Kepler-féle távcsô, optikai kérdésekkel is foglalkozik, felírja – közelítô jelleggel – a törés törvényét: a pontos képlet felállítása Descartes-ra és Snelliusra vár, de elegendô pontos ahhoz, hogy már tudományos alapon konstruálhassa meg a maga távcsövét. Foglalkozott matematikával is, így a hordók térfogatának számításával, ahol meggondolásaiban szinte az infinitezimális számítások alapjáig jutott el. Legnagyobb eredményének ô maga a világ harmóniáját kifejezô törvényt tartja, amelyet ma Kepler harmadik törvényeként ismerünk: A bolygók keringési ideinek négyzetei úgy aránylanak egymáshoz, mint a középnaptávolságok köbei.

Élvezzük vele együtt a megtalálás örömét:

Most. miután 18 hónappal ezelôtt az elsô hajnali derengés, három hónappal ezelôtt a reggeli világosság, pár nappal ezelôtt viszont már a ragyogó nap világította meg ezt a csodálatos színjátékot, semmi sem tart vissza: igen, szent ôrjöngés vesz erôt rajtam. Fölényesen dacolok a halandókkal, nyíltan bevallva: megloptam az egyiptomiak aranyedényeit, hogy Istenemnek szentelt hajlékot építsek azokból messze túl Egyiptom határain. Bocsássatok meg nekem, hogy így örülök. Ám haragudjatok, azt is elviselem. Rajta, elvetem a kockát és könyvet írok a jelennek vagy az utókornak. Nekem mindegy! Ám várjon száz évig olvasójára; nem várt-e az lsten is hatezer évig, míg bennem értôjére lelt?!
 

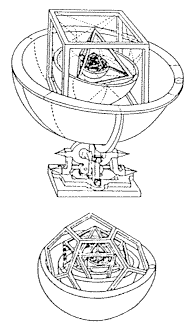Így képzelte Kepler a hat bolygó pályájának, valamint az öt szabályos testnek a kapcsolatát. Mindenek mértéke a Föld szférája. Rajzolj  köréje egy dodekaédert: a köréje írt szféra lesz a Marsé. Rajzolj most egy tetraédert a Mars szférája körül: ezen tetraéder köré írt szféra lesz a Jupiteré. Írj egy kockát a  Jupiter szférája köré: ezen kocka köré írt  szféra a Szaturnuszhoz tartozik. És most rajzolj a Föld szférájának belsejébe egy ikozaédert: az ebbe írt szféra a Vénuszé. Rajzolj egy oktaédert a Vénusz szférájába: az ebbe berajzolt szféra lesz a Merkúr szférája. Íme, ez a magyarázata a bolygók számának. (Kepler: Mysterium Cosmographicum, 1596) A térbeli ábrázolás Christophorus Leibfried (1597) mûve

Miszticizmusra való hajlandóságát a még fiatal korában, 1596-ban megjelent mûve, a Mysterium Cosmographicum dokumentálja. Ezt a mûvét öreg korában sem tagadta meg, legalábbis az érdemi mondanivalóját illetôen; jóllehet itt még a kopernikuszi körpályák, sôt az epiciklusok is szerepelnek. Ebben a könyvben Kepler arra a kérdésre szeretne választ kapni, hogy a Nap körül miért éppen 6 bolygó kering és miért pontosan a megadott távolságokban. Ma mosolygunk a kérdésfeltevésen: a bolygók száma is megnôtt azóta és elvben bármely távolságban – a megfelelô keringési idôvel – mozoghatna egy bolygó. Kepler azonban azt tette, amit minden fizikus tenni szokott: a tények adottak – a 6 bolygószám és a távolságaik – és mindez magyarázatra szorul. Kepler megtalálni vélte a feleletet. Úgy gondolta, hogy Isten a világ teremtésénél a platóni 5 szabályos testet tartotta szem elôtt és annak alapján konstruálta a Naprenszert. A Nap köré rendre elhelyezte az oktaédert, ikozaédert, dodekaédert, tetraédert, majd végül a kockát, és az ezekbe, ill. köré rajzolt szférák adják rendre az egyes bolygók szféráit. Így adódtak ki a meghatározott pályasugarak és a hatos bolygószám. A meglepô az, hogy ezen mesterkélt elrendezésbôl adódó távolsági viszonyok többé-kevésbé megfeleltek a valóságnak.

Mint említettük, ma mosolygunk a kérdésfeltevésen, és még inkább mosolygunk a megoldáson. Pedig éppen egy atomfizikus számára nem lehet idegen ez a fajta okoskodás. Mert mirôl is van szó? Egy szimmetriaelv segítségével – az 5 platóni test szimmetriaelveket testesít meg – pályákat tüntetünk ki és arra egyetlenegy, tehát meghatározott számú bolygót helyezhetünk el: ez az utasítás úgy hangzik, mint az atom esetében a Bohr-féle kiválasztási szabály, kombinálva a Pauli-elvvel. A 20. század elején azt mondjuk, hogy az atom tulajdonképpen egy Naprendszer, azzal a különbséggel, hogy az atom elektronjai nem mozoghatnak tetszés szerinti pályán és azon tetszés szerinti számban. Ha azonban ehhez a Kepler-féle elképzeléshez nyúlnánk vissza, az analógia teljes Ienne.

A 17. század elsô évtizedének fôszereplôi: Galilei Rómában, Kepler Prágában. Már Galilei maga is aggódott, hogy az egyházi üldöztetés miatt a tudományos haladás súlypontja az Alpokon túlra, északra helyezôdik át. A súlyponteltolódást azonban nem lehet erre az egy okra visszavezetni: már az inkvizíciós per elôtt, északon és nyugaton, elsôsorban a protestáns Angliában, Hollandiában, de a "nagyon" katolikus Franciaországban is megindult az erjedés. Hogy csak két nevet említsünk, az angol Gilbert, a mágneses jelenségek kutatója 1600-ban megjelent De Magnete címû könyvének bevezetôjében már ugyanolyan természetfilozófiai elveket vall, mint késôbb Galilei. Descartes pedig a megdöntött arisztotelészi filozóliai rendszer helyett egy ugyanolyan teljességre törekvô, mindenre választ adni akaró modern világnézetet atkotott.

Az új gondolkodást tehát már nem lehetett feltartóztatni – hogy újból Einsteint idézzük, akár Galileivel, akár Galilei nélkül is.

Búcsúzóul a kortól, két üzenet az utókornak, vagy ha úgy tetszik a mának, egy-egy a két fôszereplôtôl.

Már Platón azt hirdette, hogy nem értheti meg valaki az ideák világát, ha nem tud geometriát. Galilei, a józan, a pragmatikus így vélekedik:

A filozófia abban a nagy könyvben van írva, amely nyitva áll mindenkor szemeink elôtt: az univerzumra gondolok; .de nem olvashatjuk mindaddig, míg meg nem tanultuk a nyelvét, és nem barátkoztunk meg a jelekkel, amelyekkel írva van. A matematika nyelvén van írva és a betûi háromszögek, körök és más geometriai alakzatok, melyek ismerete nélkül lehetetlen egyetlen szót is megérteni.

Végül Kepler, akit néha elragad a fantáziája, aki néha a fellegekben jár és ezért sokunkhoz nagyon közel áll, ezt üzeni hasznosságorientált korunknak:

Dehát muszáj az isteni dolgok értékét garasokban mérni, akár egy tál levesét?! Ugyan kérem – szinte hallom az ellenvetést, mit használ egy éhes gyomornak a természet ismerete, mit az egész asztronómia ismerete?! Az értelmes emberek azonban ne hallgassanak a tudatlanságra, mely azt harsogja, hogy minden ilyen stúdiummal fel kell hagyni! Az ember megbecsüli a festôt, mert a szemet, a Zenészt, mert a fület gyönyörködteti, jóllehet egyéb hasznot nem hoznak számunkra. Igen, az az élvezet, amelyet alkotásaikban nyerünk, nemcsak méltó az emberhez, de egyenesen tisztességére szolgál. Minô tudatlanság, minô ostobaság megtagadni a szellemtôl a neki szánt tiszteletre méltó örömet. A természet ellen hadakozik, aki ezen gyönyörök ellen hadakozik. Vajon a jóságos Teremtô, aki a természetet a semmibôl a létbe hívta, nem adta-e meg minden teremtménynek azt, ami szükséges, sôt ezenkívül díszt és vidámságot pazarló bôségben! Vajon éppen az emberi szellemet, Isten saját képmását hagyta volna boldogító gyönyör nélkül?

Alapos okunk van azt állítani, a természeti jelenségek sokfélesége azért olyan nagy, az égbolton elrejtett kincsek azért olyan gazdagok, hogy az emberi szellem számára a friss táplálék sohase fogyjon el, hogy ne unhassa meg a régit és ne nyugodhasson meg, hanem inkább szellemének gyakorlására új és új mûhelyt találjon.