Az algoritmusok bonyolultsága
Mi az, hogy algoritmus? Amikor Clinton elnök szaxofonozik, és Al Gore alelnök az ujjaival dobol hozzá az asztalon. A valódi meghatározás ennél jóval nehezebb. Nem matematikai megfogalmazásban azt lehet mondani, hogy egy pontos szabályok szerint elvégzett elemi mûveletekbõl álló mûveletsor, ahol az intuíciónak nincs szerepe. Lássunk példákat.
Vizsgáljuk két, tízes számrendszerben felírt szám összeadását. Az egyik elemi mûvelet az, hogy két egyjegyû számot adunk össze. Ezeket az összegeket számolás nélkül, „kívülrõl tudjuk”. A másik elemi mûvelet pedig egy szám eggyel való növelése. Ezek után az összeadás az iskolai szabályok szerint végezhetõ. Ha az egyesek helyén álló számok összege egyjegyû, akkor a következõ helyi értéket vesszük, ha „marad” 1, akkor azt „átvisszük”. Nem érdemes a szabályokat precízen leírni, hiszen mindenki pontosan ismeri azokat. Figyeljük meg azonban, hogy a szabályok száma véges, mégis, akármekkora számokat képesek vagyunk így összeadni.
Egy másik példa a kémiai analízis. Tegyük fel, tudjuk, hogy egyetlen fajta só vizes oldata van birtokunkban. Elemi mûveletek egész sorát ismerjük: valamilyen reagenst hozzáöntünk, és megfigyeljük, hogy milyen színûvé válik az oldat. Rendelkezésünkre áll egy pontos táblázat, melybõl meghatározhatjuk, hogy adott eredmények után melyik reagenst kell használni. A táblázat úgy van megalkotva, hogy sok-sok lépés után végül egyértelmûen meg tudjuk állapítani, melyik só oldata a kérdéses. Itt sem támaszkodhatunk az intuíciónkra.
Végül egy példa a számítógépes könyvtári katalógusról. Ki kell keresni az M. Lewinsky által írt könyveket. Tegyük fel az egyszerûség kedvéért, hogy a könyvek a szerzõk neve szerint betûrendben vannak felsorolva. Egy lehetséges algoritmus a következõ. Az elejétõl kezdve hasonlítsuk össze a Lewinsky nevet minden szerzõ nevével. Elõbb-utóbb elérkezünk a megfelelõ helyre, tehát az algoritmus eredményes lesz. Nézzünk azonban egy másik algoritmust is. Megnézzük a keresett szó elsõ betûjét, az L-et. A mûvek sorrendjében kijelöljük az L betûvel kezdõdõ szerzõjû mûvek halmazának az elejét és végét. Ezek után ismételjük meg ugyanezt a második, majd harmadik stb. betûvel. Látható, hogy a második algoritmus legtöbbször jóval gyorsabb. (Az elsõ gyorsabb, ha pl. a keresett szerzõ neve Aachs.)
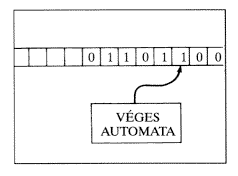
1. ábra
Ha a fenti, és az általunk ismert számos példa alapján értjük is, hogy mi az algoritmus, az elsõ bekezdésben adott meghatározás nem alkalmas arra, hogy annak alapján matematikailag pontos állításokat tegyünk, sõt bizonyítsunk. Turing angol matematikus (1912–1954) még a számítógépek elterjedése elõtt hozott létre egy modellt az emberi algoritmikus gondolkozás leírására. Ezt a modellt Turing-gépnek hívjuk. Ismertetéséhez elõbb a véges automata fogalmára van szükségünk. A pontos definíció helyett gondoljunk egy véges sok alkatrészbõl álló berendezésre, ami véges sok- féle jelet képes befogadni, és véges sok- féle jelet tud „kiírni”. Ilyen pl. egy jegykiadó automata. A bemenõ jelek a bedobott érmék, a kimenõ jelek pedig a kiadott jegyek. Ami nagyon fontos: bármilyen sok alkatrésze is van ennek az automatának, a belsõ állapotainak száma véges. A Turing-gép áll egy mindkét irányban végtelen szalagból, ami kis kockákra van osztva, és egy véges automatából, aminek író-olvasó feje a szalagon fut (1. ábra). Az automata egy kiinduló állapotból indul, elolvassa a jelet, amit lát, a belsõ állapotának és az olvasott jelnek a függvényében kiír egy új jelet a régi helyére, az olvasófejet vagy balra, vagy jobbra elmozdítja, vagy helybenhagyja, és a belsõ állapotát is átviszi egy új állapotba. Ezek után megismétli ugyanezt, már az új belsõ állapot és az új olvasott jel alapján, és így tovább, egészen addig, míg egy olyan belsõ állapotba kerül, amit végállapotnak nevezünk, ekkor a gép megáll, befejezte a számítást. Ami a szalagra eredetileg volt írva, az a bemenõ sorozat, vagy input, ami megállás után áll a szalagon, az a számítás eredménye, másképpen az output.
Ha két szám összeadását akarjuk e géppel elvégezni, akkor legyenek a szalagra írható jelek az egyjegyû számok, meg egy „üres jel”. A szalagon számolás elõtt a két összeadandó szám áll, közöttük egy üres jel, a számok elõtt és után üres jelek állnak a végtelenségig. A véges automatában pedig benne vannak az elemi mûveletek, az „átvivés”, és annak leírása, hogy a fejet ide-oda kell mozgatni a két szám között. Elég kellemetlen feladat ennek a véges automatának a függvényeit megadni, de elvileg nem nehéz. A megállás után a két összeadandót követõ üres jel után fog az eredmény állni.
Nem lehetne-e ezt az összeadást csupán egy véges automatával megcsinálni. Nyilván nem, hiszen a mûveletnek akármilyen hosszú számokra is mûködnie kell, de a véges automatának csak véges sok állapota lehet. Tehát bármely két szám összeadását le lehetne írni egy véges automatával, de az összeadandók méretével az automata is nõne. Nekünk meg csak egy fix automatánk lehet.
De le lehet-e valóban írni egy Turing-géppel bármely algoritmust, amit algoritmusnak gondolunk. A tapasztalat azt mutatja, hogy igen. Eddig még senki nem tudott olyan algoritmus adni, amit nem lehetett Turing-géppel utánozni. Ezt matematikailag természetesen nem lehet bebizonyítani, hiszen az algoritmus heurisztikus fogalma nem fogható meg matematikailag. Ennek ellenére meg van fogalmazva, majdnem úgy, mint egy tétel. Úgy nevezik, hogy Church-tézis, amely szerint minden algoritmikus feladat elvégezhetõ Turing-géppel.
Az algoritmusok sebessége
Miután matematikai formában megfogalmaztuk, hogy mit értünk algoritmus alatt, rátérhetünk az algoritmusok tanulmányozására. Ezentúl természetesen algoritmus alatt mindig egy Turing-géppel leírható eljárást értünk.
A könyvtáras példa mutatja, hogy egy adott feladat esetén nem egyszerûen az a cél, hogy találjunk rá egy algoritmust, hanem az is fontos, hogy az algoritmus (Turing-gép) lépésszáma a lehetõ legkevesebb legyen. Természetesen gyakorlati feladatoknál az is lényeges eredmény, ha a lépésszámot sikerül megfelezni, de sokkal lényegesebb elvi problémára fogunk rámutatni ezzel kapcsolatban. Tekintsünk ismét néhány példát.
Kompánia országról tudjuk, hogy kik utálják egymást, tehát bármely két emberrõl lehet tudni, hogy utálják egymást vagy nem. Ezt ábrázolhatjuk egy ún. gráffal, amely pontokból és összekötésekbõl áll. A pontok embereket jelképeznek, az összekötések az utálatot. Ezt a gráfot az ország „utálat-gráfjának'' nevezhetjük. Az algoritmikus feladat az, hogy el kell dönteni, hogy beosztható-e az egész ország két pártra úgy, hogy az egy pártban levõk ne utálják egymást. Jelöljük az egyik pártot 0-val, a másikat pedig 1-gyel. (A 0 esetén ne gondoljunk egyik magyar pártra se, az 1 pedig nem célzás az egypártrendszerre.) Az ország pártokra való felosztását tehát úgy képzelhetjük el, hogy az ország utálatgráfjában a pontokat (embereket) megjelöljük 0-val vagy 1-gyel. Ezt a matematikában úgy mondjuk, hogy a gráfot „kiszínezzük” a 0 és az 1 „színekkel”(2. ábra). Tehát problémánk átfogalmazva úgy szól, hogy egy adott gráf kiszínezhetõ-e két színnel úgy, hogy az összekötött pontok ne legyenek azonos színûek.

2. ábra
A legtermészetesebb ötlet az, hogy minden lehetséges színezést kipróbálunk. Minden pontot kétféle színnel (0 vagy 1) színezhetünk, minden pontnál két lehetõséget választhatunk, azaz a színezések száma 2·2·2….=2n. Ha a színezéssel megvagyunk, akkor könnyen ellenõrizhetõ, hogy nincsenek-e azonos színû pontok összekötve. Ez a módszer valóban nagyon egyszerû, csak kicsit sokáig tart. Ha például Kompánia lakosainak száma 100, akkor 2100 színezés van. Ha egy színezéshez egymilliomod másodperc kell, akkor az összes színezéshez 294 másodperc, azaz 1,157·1089 nap. Algoritmusunk elvileg mûködik, de gyakorlatilag kivitelezhetetlen.

3. ábra
Van azonban egy sokkal gyorsabb algoritmus. Színezzük ki az egyik pontot például 0-val. Szomszédait akkor 1-gyel kell, színezzük is ki õket. Ugyanígy folytassuk, színezzük a szomszédokat az ellenkezõ színnel (3. ábra). Elõfordulhat, hogy pl. egy 0 színû pont szomszédja már 0-val van színezve. Ez az ellentmondás azt bizonyítja, hogy a gráfot nem lehet két színnel kiszínezni, azaz az országot két pártra osztani. Ha viszont sikerül az eljárást ilyen ellentmondás nélkül befejezni, akkor megvan a felosztás. Hány lépés kell ehhez? Legfeljebb annyi, ahány összekötés (az összekötést élnek nevezzük) lehet a gráfban, vagyis ahány pontpár van. Ha a pontszám 100, akkor összesen 100·99/2=4950 a párok száma. Ez tehát egy valóban végrehajtható algoritmus.
Most megpróbáljuk megfogalmazni, hogy mit nevezünk jó, illetve rossz algoritmusnak a lépések száma szempontjából. A fenti példában adott pontszámra persze meg tudjuk állapítani, hogy az egyik lépésszáma nagyobb, mint a másiké, de minõségbeli különbséget csak akkor tudunk megállapítani, ha a probléma méretét (pontok számát) általánosan tekintjük. Legyen tehát a pontok száma n. Az elsõ, rossz algoritmusnál a lépésszám 2n, a második, jó algoritmusnál n(n-1). Az elsõ függvény exponenciális, tehát n-nel nagyon gyorsan nõ, a második pedig négyzetes, ami sokkal lassabban. Ha a lépésszám pl. n5 volna, még az is sokkal lassabban nõ, mint az exponenciális függvény, és gyakorlatilag még mindig végrehajtható. Tehát a választó vonal legyen az, hogy az algoritmus lépésszáma korlátozható-e egy nk függvénnyel, ahol k egy rögzített szám. Ekkor azt mondjuk, hogy az algoritmus polinomiális. Az ilyenek a jó algoritmusok. Ha a lépésszám exponenciális, akkor az algoritmus rossz. Meg kell azonban még pontosabban gondolni, hogy mi játssza általában egy problémánál az n szerepét. A bemenõ adatok száma. Amit meg kell adni ahhoz, hogy probléma teljesen le legyen írva. A fenti gráfos példában nem elég a pontokat felsorolni, meg kell adni, hogy melyik pontok vannak összekötve, melyek nincsenek. Azaz a bemenõ adatok száma valójában négyzetes függvénye n-nek. Könnyen látható, hogy ez nem változtat a helyzeten, a jónak, illetve rossznak nevezett algoritmusok ennek függvényében is polinomiális illetve exponenciális sok lépést igényelnek.
Ezek után már lényegében matematikai pontossággal meg tudjuk határozni egy algoritmus jóságát. Tegyük fel, hogy van egy probléma-családunk (tulajdonképpen ez csak egy probléma, de minden n-re van egy), és annak megoldására egy algoritmus, matematikailag egy Turing-gép. Jelöljük n-nel a bemenõ adatok számát, azaz legyen n azon jelek száma, amelyek a Turing-gép szalagján kezdetben állnak. Ha a Turing-gép f(n) lépésben mindig be tudja fejezni a számolást, és kiírja szalagjára az eredményt, de ennél gyorsabban (peches esetben) nem, akkor az algoritmus bonyolultsága f(n). Ha f(n) egy polinom, akkor az algoritmus polinomiális, ha f(n) exponenciális, akkor az algoritmust exponenciálisnak nevezzük.
Nehéz problémák
Nézzünk most egy másik, Kompániára vonatkozó feladatot. Azt akarjuk eldönteni, hogy beosztható-e az ország lakossága három pártra úgy, hogy az egy pártba kerülõk ne utálják egymást. Matematikai nyelven: adott egy gráf. Kiszínezhetõ-e a gráf három színnel úgy, hogy az egyszínû pontok között ne legyen él(összekötés). A 4. és 5. ábrán három színnel színezhetõ illetve nem színezhetõ gráfok láthatók. A korábbi, két színnel való színezésre lehetett exponenciális, de polinomiális algoritmust is találni. Itt ez nem megy. Nem ismeretes olyan algoritmus, amely exponenciálisnál gyorsabban döntené el a három színnel való színezhetõséget. Ha igaz, hogy nincs is, akkor nemcsak az algoritmus rossz, hosszú, hanem maga a probléma is nehéz. De ezt eddig csak sejthetjük. Szemben a gráf kettõ-színezésével, ami egy polinomiális probléma, mert van megoldására polinomiális algoritmus.

4. és 5. ábra
Egy másik ismert probléma a független pontok problémája. Kezdjük egy játékos példával. Megadható-e a sakktáblán 8 vezér úgy, hogy ne üssék egymást? A 6. ábra mutatja, hogy ez lehetséges, de aki maga próbálta ezt a rejtvényt megfejteni, tudja, hogy nem olyan könnyû az elhelyezést megtalálni. Ez a feladat is megfogalmazható a gráfok nyelvén. A sakktábla mezõi legyenek a gráf pontjai, két ilyen pontot (mezõt) kössünk össze egy éllel, ha az egyik mezõrõl a vezér egy lépéssel el tud jutni a másikba, azaz a másik mezõt „ütni” tudja. Az általános, már gráfokra vonatkozó probléma így szól: adott egy gráf és egy k egész szám, eldöntendõ, hogy ki lehet-e választani a gráfból k pontot úgy, hogy ezek között a pontok között ne legyen összeköttetés. A probléma inputja tehát most nem csak egy gráf, hanem még egy egész szám is hozzátartozik. De mivel a probléma csak akkor érdekes, ha ez az egész szám kisebb a pontok számánál, elég a megoldás sebességét a gráf pontjai (pontosabban élei) számának függvényében nézni, mert az egész szám ebbe „belefér”. Erre a problémára sem ismert exponenciálisnál rövidebb algoritmus, tehát ez is egy nehéz probléma.

6. ábra
Most megmutatjuk, hogy ha a független pontok problémáját meg tudnánk oldani polinomiális sok lépésben, akkor a három színnel való színezhetõség problémáját is meg tudnánk oldani. Legyen G az az n pontú gráf, amelyrõl el kell döntenünk, hogy kiszínezhetõ-e három színnel. Csináljunk belõle egy H gráfot a következõképpen. Vegyük G három különálló példányát, de kössük össze azokat a pontokat, amelyek G-ben ugyanazok voltak. Lásd a 7. és 8. ábrákat, ahol elõbb azt ábrázoltuk, ha G a 4. ábrán szereplõ 5 hosszú kör, majd az általános esetet próbáltuk illusztrálni. Ha G három színnel kiszínezhetõ, vegyünk egy ilyen színezést, H egyik példányából vegyük ki a 0 színû, a másik példányából az 1 színû, végül a harmadik példányból a 2 színûeket. Ekkor a 3n pontú H-ból kivettünk n pontot úgy, hogy ezek között nincsenek öszszekötések, vagyis n független pontot találtunk. Ezt a a kiválasztást (a 4. ábra színezése alapján) a 7. ábrán meg is adtuk. A 8. ábrán az olvasó képzeletére bíztuk. Másrészt az is könnyen meggondolható, hogy ha H-ban ki tudunk választani n független pontot, akkor ez megadja G három színnel való színezését. (H három olyan pontja, ami egy G-beli pontból lett, páronként össze van kötve, tehát ezek közül csak egy lehet kiválasztva. Mivel n pontot választottunk H-ból, minden ilyen ponthármasból ki is kellett egyet választani. Az, hogy G melyik példányából vettük a pontot, megadja a G-beli pont színezését.) Ezzel azt a kis matematikai tételt bizonyítottuk, hogy G akkor és csak akkor színezhetõ ki három színnel, ha H-ból kiválasztható n független pont. Tegyük most fel, hogy van polinomiális algoritmusunk a független pontok kiválasztására, és egy G gráfról azt kell eldöntenünk, hogy kiszínezhetõ-e három színnel. G-bõl elkészítjük a H gráfot, ehhez polinomiális sok lépés kell, ezután H-ról eldöntjük, hogy van-e benne n (G pontjainak száma) független pont. A kis tétel szerint ezzel azt is eldöntöttük, hogy G színezhetõ-e három színnel. Azt mondjuk, hogy a három színnel színezhetõség problémája polinomiálisan visszavezethetõ a független pontok problémájára.

7. és 8. ábra
De ez fordítva is igaz: a független pontok problémája is (polinomiálisan) viszszavezethetõ a három színnel való színezés problémájára. Vagyis, ha az egyik problémára csak exponenciális sok lépésbõl álló algoritmus van, akkor a másikra is, tehát a két probléma egyforma nehéz, pontosabban fogalmazva polinomiálisan ekvivalensek.
Egy további neves probléma a Hamilton-körök
problémája. Adott egy gráf, végig tudunk-e
menni a gráf élein úgy, hogy minden pontot pontosan
egyszer érintve visszakerüljünk a kiinduló ponthoz.
Szemléltetve: egy ügynök végig tud-e utazni az
összes városon úgy, hogy csak az egymással közvetlen
repülõjárattal összekötött városok
között repülhet, és minden városban pont egyszer
lehet, végül hazaér. De itt is van „sakkos” példa:
végig lehet-e menni a sakktáblán lóugrásokkal
úgy, hogy a végén a kiindulópontba kerüljünk
vissza? A 9. ábra gráfjában
létezik Hamilton-kör, az ügynök a pontokon a számozás
szerint mehet. Az 10. ábrán
egy olyan gráf látható, amiben nincs Hamilton-kör;
ez egy kis próbálgatással ellenõrizhetõ.
Erre a problémára szintén nem ismeretes exponenciálisnál
rövidebb algoritmus, tehát ez is egy nehéz probléma.
Errõl a problémáról is matematikailag precízen
bebizonyítható, a fentiekhez hasonló visszavezetésekkel,
hogy polinomiálisan ekivivalens mind a három színnel
való színezés problémájával,
mind pedig a független pontok problémájával.
Persze ezek a visszavezetések nem mindig olyan egyszerûek,
mint a fenti esetben. Sokszor igen bonyolultak, mi itt kénytelenek
voltunk a legegyszerûbbek egyikét bemutatni.
 |
 |
| 9. ábra | 10. ábra |
Tehát mát három problémánk van, amelyek egyikére sem ismerünk polinomiális algoritmust, de azt tudjuk, hogy ezek egyszerre polinomiálisak, vagy exponenciálisak. Csak az a kár, hogy egyikrõl sem tudjuk!
Nézzük meg alaposabban, milyen probléma volt az említett három. Elõször is eldöntendõ kérdések voltak. Az eredmény igen, vagy nem. A Turing-gépen a végeredmény egy 0 vagy 1. Az összeadás problémája nem ilyen, ott az eredmény egy hosszabb sorozat. De az ilyen eldöntendõ problémák bizonyos értelemben a legjellemzõbbek, és sok más probléma visszavezethetõ rájuk. A másik, lényegesebb tulajdonságot illusztráljuk elõször a három színnel való színezés problémáján, vagy eredeti megfogalmazásában, az ország három pártra való osztásán. Ha a helyes felosztást, amelyben nincsenek egy párton belül utálat-élek, bizonyos „kormányhoz közeli körök” „kiszivárogtatják”, akkor már könnyen (polinomiális sok lépésben) ellenõrizni tudjuk, megfelelõ-e a felosztás. Hiszen csak azt kell megnézni minden élre, hogy végpontjai nincsenek-e azonos pártban. A független pontok problémájánál ugyancsak, ha egy zseniális megérzéssel valaki megsejti, hogyan lehet kiválasztania k független pontot, akkor megint könnyen ellenõrizhetõ, jó-e a kiválasztás. Végül, ha az utazó ügynöknek megjósolják, hogyan kell végigjárnia a városokat (Hamilton-kör), akkor is csak azt kell ellenõrizni, hogy a felsorolás szerinti sorrendben a szomszédos pontok össze vannak-e kötve éllel. Természetesen a lehetséges „kiszivárogtatások számának” nagynak kell lennie. Ha polinomiális lenne, az egészet polinomiális sok lépésben végigpróbálgathatnánk. De a lehetséges megoldások száma túl nagy se lehet, legfeljebb exponenciális – 2p(n), ahol p(n) egy polinom –, hiszen egy ilyen megoldást polinomiális sok lépésben akarunk ellenõrizni, tehát szükségképpen leírható polinomiális sok jellel. A leírt tulajdonságú problémák seregét NP-vel jelöljük. Matematikailag pontosan a nem determinisztikus Turing-géppel határozzuk meg. Ez nagyon hasonló a Turing-géphez, de minden helyzetben, amikor valami történik vele (új állapot, egy jel felírása a szalagra, lépés a szalagon), választhat. Például az adott állapotban, adott jelet olvasván nem egyértelmûen meghatározott az új állapota, hanem fel van sorolva, milyen új állapotokat vehet fel. A jegykiadó (véges) automata például vagy ad ki jegyet, vagy nem. De belül is vannak eltérõ lehetõségek. A pénz nem esik le vagy leesik. Ennél a nem determinisztikus Turing-gépnél az összes lehetséges mûködést tekintjük. És azt várjuk el tõle, hogy ha problémánknak van megoldása, legyen a gépnek olyan mûködése a sok lehetségesbõl, aminek a végén a szalagon egy 1-es marad, ellenkezõ esetben nincs ilyen mûködése. A három színnel színezés problémájánál ezt úgy képzelhetjük el (a nem determinisztikus Turing-gép pontos leírása igen hosszadalmas és kellemetlen lenne), hogy a gép ad egy színt a gráf elsõ pontjának (választási lehetõség!), majd a másodiknak stb., amikor már mindegyiknek adott színt, megvizsgálja, jó-e a színezés, nincs-e összekötve két azonos színû pont. Ha jó, akkor 1-et ír, különben 0-t. Egy problémáról akkor mondjuk, hogy NP-beli, ha van hozzá olyan nem determinisztikus Turing-gép, amely a gép valamelyik mûködése esetén polinomiális sok lépés után 1-et ír a szalagra, ha van megoldása a problémának, ha pedig nincs, akkor ez semelyik mûködésnél sem fordulhat elõ. Ezek után már nyilvánvaló, hogy az NP betûk nem determinisztikusan polinomiális kifejezésbõl származnak.
NP-ben centrális szerepet játszik egy további probléma, a kielégíthetõség problémája. Pontos definíció helyett csak illusztráljuk a könyvtári katalógus példáján. (A probléma nevének, és az elõzõ könyvtári példában szereplõ Lewinsky névnek az összekapcsolása téves asszociáció!) Legyen a probléma az, hogy meg kell állapítani, van-e olyan könyv a könyvtárban, amely szerzõjének a neve vagy L-lel kezdõdik, vagy Y-nal végzõdik, ezen kívül amerikai kiadó adta ki, a borítója vagy rózsaszín, vagy bordó stb. Itt a feltételek száma n, ez a bemenõ adatok száma, és a feltételek és-sel és vagy-gyal vannak összekötve, bármilyen zárójelezés mellett (fontos, hogy egy tulajdonság több helyen is szerepelhet!). Ez is polinomiálisan ekvivalens a fenti hárommal. Ezen túl, az is be van bizonyítva, amint azt az olvasó érezheti, hogy ennél nehezebb probléma az NP halmazban nincs is, tehát minden NP-beli probléma visszavezethetõ a kielégíthetõségi problémára.
De nem csak ez a négy probléma vezethetõ vissza egymásra. Több tízezer NP-beli problémáról sikerült bebizonyítani, hogy ezek mind-mind polinomiálisan ekvivalensek. Ha egyikük polinomiális, akkor a többi is, ha egyikük exponenciális, akkor mind-mind az. Valóban felháborító, hogy ezt nem tudjuk egyikkõjükrõl sem! Ezek tehát az NP „krémje”, a legnehezebbek NP-ben. ’ket NP-teljes problémáknak szoktuk nevezni.
A nagy kérdés
P-vel szokás jelölni azon NP-beli problémákat, amelyek polinomiális sok lépésben megoldhatók. Az, hogy P részhalmaza NP-nek, az nyilvánvaló. A nagy kérdés tehát ilyen jelölésben fogalmazva az, hogy a „krém” valóban nehezebb-e a többinél, hiszen eddigi tudásunk szerint (elvileg) lehetséges, hogy NP minden eleme P-ben van. A nagy kérdés tehát az, hogy P=NP, vagy P=/NP. Ez ma az elméleti számítástudománynak (de talán magának a matematikának is) fõ kérdése. Természetesen a többség úgy véli, hogy P=/NP. Annyira, hogy amikor egy nem túl neves matematikus egy 40 oldalas cikkben az ellenkezõjét bizonyította, senki se akarta vállalni az ellenõrzést, sajnálták az idejüket fecsérelni egy hibás cikkel. Három évig tartott, míg valaki megmutatta a hibát. A kutatók persze azért is elfogultak, mert P=/NP esetén egy érdekes, jelentõs elmélet válna értéktelenné.
De ne higgyük azt, hogy minden NP-beli problémáról el van döntve, hogy P-beli vagy NP-teljes. Annak eldöntése pl., hogy egy adott egész szám prím-e vagy sem, egy kivétel. Nem ismeretes rá polinomiális lépésszámú algoritmus, de azt se tudjuk róla, hogy NP-teljes-e. Tehát lehetséges, hogy van rá polinomiális algoritmus, de meglehet, hogy (P=/NP esetén) csak exponenciális algoritmus van rá. Ez azért izgalmas, mert sok titkosírás az egészek prímekre való felbontásán alapszik, tehát ha valaki talál egy polinomiális algoritmust e problémára, meg tud fejteni sok titkos üzenetet, amiket eddig (polinomiális idõben) megfejthetetlennek véltek.
Mit kezdjünk a nehéz problémákkal?
Mit tegyünk, ha a probléma, amit meg kell oldani, NP-teljes? Sokan azt gondolják, hogy az elméleti tudós erre azt válaszolja, hogy sajnálja, nem lehet megoldani, foglalkozzunk valami mással, õt ez nem érdekli. A helyzet nem így áll. Elméleti kutatók serege keresi a választ az ilyen helyzetekre. Hadd vázoljunk néhány ötletet.
(1) Lehetséges, hogy az objektum, amit vizsgálunk, rendelkezik valamilyen speciális tulajdonsággal, amit feltéve, már polinomiális lesz a probléma. Például, ha a három színnel való színezhetõség problémájánál feltesszük, hogy a gráf minden pontjának legfeljebb két szomszédja van (azaz mindenki legfeljebb két embert utál, boldog ország!), akkor nem is kell semmit számolni, máris tudjuk, hogy a gráf kiszínezhetõ három színnel, amint ez könnyen végiggondolható. Ha minden pontnak legfeljebb három szomszédja van, akkor egy matematikai tétel (Brooks tétele) segítségével nagyon egyszerû módon eldönthetõ, hogy kiszínezhetõ-e gráfunk három színnel, mert a nemleges válasz ez esetben csak nagyon kivételes esetben lehetséges.
(2) Megelégszünk egy közelítõ megoldással. Például a Hamilton-kör esetén azt vizsgáljuk, van-e olyan körút az ügynök számára, amely a pontok legfeljebb felén halad át kétszer. A gyakorlati alkalmazásokban az ilyen közelítés legtöbbször megfelelõ (különösen akkor, ha jobb nincs), és a probléma ilyen módosítása gyakran már polinomiális. Persze nem mindig. Sajnos ismeretes sok probléma, aminek közelítõs változata is NP-teljes.
(3) A legmerészebb ötlet az, hogy olyan számítógépet kell találni, amely megvalósítható, és annak modelljén már el lehet végezni az NP-teljes problémák megoldását. A Church-tézis szerint a Turing-géppel minden algoritmus elvégezhetõ, de ez nem jelenti azt, hogy a lépések számánál is elég a Turing-gépet használni. Az volna jó, ha valahogy egyszerre sok számítást tudnánk végezni párhuzamosan. Például ha egyszerre tudnánk kipróbálni egy gráf összes három színnel való kiszínezését, akkor polinomiális idõ alatt el tudnánk dönteni, hogy valamelyik jó-e. De ehhez nagyon sok alkatrész kellene, a bemenõ adatok exponenciális függvényével leírható számú. Az elvi lehetõség ott bujkál, hogy valamilyen nagyon pici, elemi részecskéket használhatnánk a számításhoz, amikbõl rengeteg áll rendelkezésre, így gyakorlatilag úgy tekinthetjük, hogy exponenciálisan sok van belõlük. Eddig két ilyen gondolat vetõdött fel.
(3.a) A kvantum-számítógép az egyik. Elve a kvantummechanika törvényein alapszik. Ilyen terjedelemben nehezen leírható módon az elemi részecskék milliói egy idõben, párhuzamosan „dolgoznának”. Eddig csak egy nagyon primitív változatot sikerült megépíteni, ami három bittel tud „számolni”. Sokan hisznek benne, hogy továbbfejleszthetõ, még többen nem hisznek ebben. Matematikai modelljét (megint csak sokkal bonyolultabb, mint a Turing-gép) is sikerült megalkotni, ami nagyon jól mûködik: sikerült vele polinom idõben eldönteni, hogy egy szám prím-e, vagy sem. (Veszély a jelenlegi titkosítási eljárásokra!)
(3.b) A másik remény a biológiai számítógép. „Mûködését” a Hamilton-kör problémáján illusztráljuk. Ismeretes, hogy vannak olyan molekulák, amelyek „karjai” szívesen kapcsolódnak bizonyos más molekulák „karjaihoz”. Ehhez hasonlók vannak pl. az orrunkban levõ szaglósejtekben, bizonyosak „csapdába ejtik” a szagokat okozó molekulákat, a sejt jelez, elkezdjük érezni a szagot. Ezt az elvet próbáljuk használni. Adott egy gráf, amirõl el akarjuk dönteni, hogy van-e benne Hamilton-kör. Készítsünk egy molekulát a gráf minden pontjához. Egy olyat, amelyik pontosan azon molekulákhoz tud, szeret csatlakozni, amelyekhez a gráfban él köti. De csak két másikhoz tud csatlakozni. Ha már kettõhöz csatlakozott, akkor már „semlegessé” válik. A 6. ábrán gráf 2-es pontjához tehát pl. egy olyan molekula szükséges, amelyik az 1-es és 3-as ponthoz rendelt molekulához kapcsolódik jól, míg a 4-eshez nem. Ha ezek a molekulák megvannak, akkor ezeket nagy számban rakjuk be egy edénybe, és keverjük össze az anyagokat alaposan. Mivel mindegyik molekulából nagyon sok van, a keverés során nagyon sok másik molekulával érintkezik, így minden lehetséges kapcsolat létrejön. Az adott gráfnak minden olyan lehetséges része (részgráf) kialakul az összekapcsolódások révén, amelyikben minden pontnak legfeljebb két szomszédja van. Így a Hamilton-kör is létrejön, ha a gráfban van ilyen. (A valószínûség számítás segítségével bizonyítható, hogy minden, ami létrejöhet, az létre is jön.) Tehát a keverés után sokféle anyag van az edényben, amelyek mindegyike egy-egy nagy, összetett molekula sok példánya. Már csak az van hátra, hogy kimutassuk, hogy az a nagy, összetett molekula, ami a Hamilton-körnek felel meg, benne van-e az edényben. Ezt vagy kémiai módon, egy reagenssel, vagy fizikai módon, a molekula súlyával mutathatjuk ki.
Tanulság?
Egy ördögi történettel fejezem be ezt a kis ismertetõt. A Sátán megkísérti a számítástudóst.
– Pénzt adok, gazdagságot, tied lesznek a legszebb nõk, a legjobb kocsik, ha engem szolgálsz.
A tudós elgondolkodik, nagyon szeretne gazdag lenni, nem is szólva a nõkrõl. De a becsület! Mégis, van valami, amiért érdemes eladni a lelkét.
– Rendben, a te szolgád leszek, ha megmondod, hogy P=NP vagy nem, és ha nem, mi a megoldás.
– Nagyszerû, nem vagy te olyan együgyû! Holnap hozom a megoldást.
A Sátán nem jön se másnap, se a rákövetkezõ héten. Csak egy hónap múlva:
– Nem megy! A Nagy Hacker mindig belép, és leállítja a számításokat!
Irodalom
Lovász László, Gács Péter: Algoritmusok, Tankönyvkiadó, 1987.
Garey, M. R., Johnson, D. S.: Computers and intractability. A guide to the theory of NP-completeness, W. H. Freeman and Comp., San Francisco, 1979.
| Természet Világa, | 2000. II. különszám
http://www.kfki.hu/chemonet/TermVil/ http://www.ch.bme.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez