A Standard Modellen túl
A részecskefizika alapvetõ célja
a világunkat felépítõ részecskék
és a közöttük ébredõ kölcsönhatások
minél egyszerûbb és egységesebb leírása.
Ennek a felfedezõ útnak egy kimagasló állomása
az elektrogyenge kölcsönhatások Standard Modellje, mely
magában foglalja az egyesített elektromágneses és
gyenge, valamint a lazán hozzáillesztett erõs kölcsönhatást.
A Standard Modell (SM) ragyogóan leírja lényegében
az összes gyorsítóban lezajló fizikai folyamatot.
Egyes fizikai mennyiségeket már ezrelék pontossággal
ismerünk a részecskefizika és az egész fizika
frontvonalának számító nagyenergiás
részecske ütközésekben. A mért eredményeket
az SM-ben összetett, kvantummechanikai tulajdonságokat is figyelembe
vevõ számolásokkal (hurokkorrekciókkal) tudjuk
reprodukálni. A kísérletek és az elméleti
számítások összhangja lélegzetelállító.
(A következõkben Horváth Dezsõ
Standard Modellt bemutató cikkének fogalmaira építünk.)
Standard Modell, hogyan tovább?
Az SM mégsem a részecskefizika végsõ
elmélete. Hiába írja le lenyûgözõ
pontossággal a mai kísérleteket, elméleti szempontból
rengeteg kivetnivalót találunk. A felmerülõ problémák
megoldására született, az SM 100 GeV energiaskálájánál
nagyobb energiákon érvényes modelleket nevezzük
a Standard Modellen túli elméleteknek. Ezeknek az utóbbi
25 évben született modelleknek alapvetõ jellemzõik:
alacsony energián (100 GeV-en) vissza kell kapnunk az SM-et, a jelenleg
és a közeljövõben megfigyelhetõ világ
négy téridõ dimenziós (3 tér + 1 idõ)
és a gravitációt csak a Planck-tömeg skáláján
tudjuk beolvasztani egy még nagyobb elméletbe. A Planck-tömegnek
(1019 GeV) megfelelõ energiaskálán a gravitációhoz
tartozó kvantumkorrekciók jelentõssé válnak
és a nem kvantumos (klasszikus) általános relativitáselméletet
végérvényesen fel kell váltsa a gravitáció
máig sem rögzített kvantumelmélete. A kvantumgravitáció
itt már egybeolvasztható a kvantumtérelméleti
nyelven megfogalmazott SM-mel, vagy annak kiterjesztett elméletével.
Így megkapnánk az összes ismert kölcsönhatást
leíró minden dolgok elméletét (az angol
rövidítés után TOE, Theory of Everything). A
Planck-skála és a minden dolgok elmélete fizikájával
ebben a cikkben már nem foglalkozunk, de a legújabb kutatások
azt mutatják, hogy ezek az elméletek lényegesen közelebb
lehetnek hozzánk és az elektrogyenge skálához,
mint ahogy azt eddig a fizikusok gondolták (lásd Csáki
Csaba cikkét).
Gondok a standard modell háza táján
A modell a kísérleti mérések és az elméleti számolások lenyûgözõ egyezése ellenére több elméleti problémát is felvet. Elsõként, a modell rendkívül sok, legalább 19 szabad paramétert tartalmaz. Egyszerû modellnél ez nem elfogadható. Ezzel kapcsolatos, hogy nem értjük, hogy az anyagterek miért fermionok és miért három családban ismétlõdnek. Úgy gondoljuk, hogy ez nem lehetett egyszerûen a természet „dadogása”, ugyanis a három a legkevesebb család, amelynél a kvarkok közötti keveredési szögekkel le tudjuk írni az alapvetõ CP-szimmetria sértését. A CP-sértés a világegyetemben található anyag-antianyag aszimmetria szükséges feltétele, de a sértés okát még nem értettük meg az elméletben. Ugyanakkor a kilencvenes évek végének munkái azt bizonyítják, hogy az SM nem képes a természetben megfigyelt anyag-antianyag szimmetria megmagyarázására. Ezt csak egy, az elektrogyenge skálától nem túl távoli új fizika tudja megtenni.
Nem értjük továbbá az elemi részek tömegspektrumát. A legutóbb felfedezett elemi rész, a top-kvark tömege 175 GeV, azaz 175 proton tömegével egyenlõ, vagyis egy nagy rendszámú, sok nukleonból álló atommal azonos tömegû. Ismeretlen az SM rendezõ elvének, a SUC(3)´SUL(2)´UY(1) mértékszimmetria-csoportjának, és a csatolási állandók értékének az eredete. A neutrínó nem kap tömeget az elméletben, jóllehet az utóbbi évek neutrínókísérletei azt mutatták, hogy van tömege. Nem világos továbbá, hogy miért kvantált az elektromos töltés, azaz miért van kapcsolat a leptonok és a kvarkok töltései között. Az SM-ben megjelenõ UY (1) hipertöltés kölcsönhatás nem lehet tetszõlegesen nagy energiáig érvényes, ugyanis az energiát növelve a kölcsönhatás egyre erõsebbé, aztán végtelenné válik. Az ilyen kölcsönhatásban, ha két részecske túlságosan nagy energiával ütközik, vagy ezzel egyenértékûen túl közel kerül egymáshoz, akkor az események kiszámíthatatlanná válnak. Az elmélet csak valamilyen véges energiáig lehet érvényes, melyet effektív elméletnek nevezünk. A részecskefizikusok az olyan kölcsönhatásokat kedvelik, amelyek egyre kisebb távolságon, avagy egyre nagyobb energián egyre gyengébbé válnak. Ezek az aszimptotikusan szabad kölcsönhatások. A SM egy korlátozott érvényességû effektív elmélet, tehát valamely nagyobb energián mindenképpen felváltja a fizika egy teljesebb leírása.
A gondok másik csoportjának forrása a Higgs-skalárbozon és a spontán szimmetriasértést leíró kölcsönhatásai, melyek az SM alapvetõ részét képezik. A Higgs-bozon az SM egyetlen, a kísérletekben mindeddig fel nem fedezett részecskéje, sõt a természetben eddig nem figyeltek meg elemi skalár részecskéket. Az SM-ben kettõ, három és négy Higgs-bozon is csatolódik egymáshoz. A 4-Higgs-csatolás a kvantumos hurokkorrekciók miatt az energiával növekszik. Egy pontban végtelenné válik, szingularitása van, ez a Landau-pólus. Az elmélet tovább már nem értelmezhetõ.
Az igazán súlyos gondot a hierarchia probléma jelenti. Hurokeffektusok révén a Higgs-bozon tömege az elméletben megtalálható legnagyobb skála, a gravitáció miatt szükségképpen megjelenõ Planck-skála nagyságú korrekciókat kap. Ezek a korrekciók destabilizálják a Higgs-bozon tömegét és az elektrogyenge kölcsönhatások skáláját. Az elméletben csak a kezdeti paraméterek rendszeres, természetellenesen pontos újrabeállításával, finomhangolásával érhetõ el, hogy az elektrogyenge skála a mérések szerinti értéken legyen. Hogy miért van az elméletben két, egymástól 17 nagyságrenddel eltérõ tömegskála, és az elektrogyenge skála miért marad alacsony a destabilizáció ellenére – ez a hierarchia probléma.
Az elsõ problémakörre a megoldást
a
nagy egyesített elméletek (angol rövidítés
után GUT, Grand Unified Theories) jelentik. A Higgs-skalár
okozta problémák enyhítésére két
megoldás kínálkozik: vagy kidobjuk a skalár
részeket az elméletbõl és mással helyettesítjük
õket – ez a dinamikai szimmetriasértés alapgondolata;
vagy, mint sokszor a részecskefizikában, a skalár
tömeg védelmében új szimmetriát és
részecskéket vezetünk be – ez vezet a ma oly népszerû
szuperszimmetrikus elméletekhez.
A nagy egyesített elmélet
A fizikusok sikeresen egyesítették még a múlt században az elektromos és a mágneses kölcsönhatást, majd jó harminc éve megszületett az elektrogyenge elmélet, az elektromágneses és a gyenge kölcsönhatás közös leírására. Az SM-ben lényegében ehhez az elmélethez jelentették a Higgs-mechanizmuson keresztül az erõs kölcsönhatást. Ezeket a kölcsönhatásokat egyaránt mértékszimmetrikus kvantumtérelméletekkel írjuk le, így kézenfekvõ azt gondolnunk, hogy ezek egy nagy egyesített elmélet (GUT) különbözõ megnyilvánulásai.
A GUT-tól azt várjuk, hogy nagy energián egy egyszerû elvek alapján felépített, mértékszimmetrikus kvantumtérelméletben néhány paraméter megválasztásával automatikusan megkapjuk az alacsonyabb energián érvényes SM-et a paramétereivel, részecskéivel, családjaival egyetemben. Mekkora energián lehet érvényes ez az elmélet? A hurokkorrekciók hatására a kölcsönhatások csatolási állandói változnak – futnak – az energia változtatásával. Az alacsony energián legnagyobb erõs csatolási állandó gyorsabban, a kisebb gyenge csatolási állandó lassabban csökken az energia növelésével, míg az UY(1) hipertöltés állandója lassan emelkedik. Felrajzolva az SM három csatolási állandójának futását, azt látjuk, hogy közel egy pontban találkoznak. Ez az energia 1015–1016 GeV, ami felett már a GUT érvényes és egy csatolási állandónk van, ami lassan csökken, ahogy azt egy nagy energiákig érvényes, aszimptotikusan szabad elmélettõl elvárjuk (1. ábra).
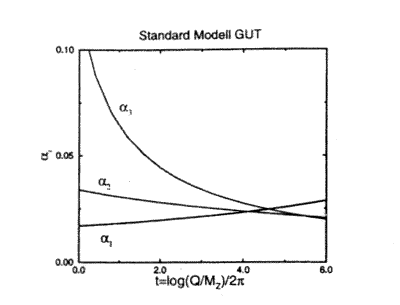
1. ábra. A három csatolási állandó változása, futása a kölcsönhatási energia függvényében
A nagy egyesített elméletek felépítésének
alapgondolata a következõ. Elõször egy olyan egyszerû
csoportot kell keresni, amely magában foglalja az SM szimmetriacsoportját
és az ismert részecskék a csoport szerint meghatározott
módon transzformálódó ábrázolásokba,
multiplettekbe rendezhetõk. Multiplettekkel („részecskesokasokkal”)
találkoztunk már az SM-cikkben , ilyenek a gyenge kölcsönhatás
szerinti dublettek (kettõsök), a gyenge mértékbozonok
alkotta triplett (hármas), az erõs kölcsönhatás
kvark színtriplettje illetve a nyolc gluon alkotta oktett. A legegyszerûbb
GUT-ok SU(5) illetve SO(10) szimmetriát mutatnak. (Ez utóbbi
a 10 dimenziós tér forgásszimmetriáját
leíró csoport, 3 térdimenziós terünkben
a megfelelõje SO(3).)
Siker és kudarc
A nagy egyesített elméletek sikereit és kudarcait a legegyszerûbb SU(5) egyesített elméleten keresztül mutatjuk be. A nagy egyesítési skála felett az elmélet SU(5) szimmetriát mutat. A GUT-skálán ez sérül, ennél kisebb energiákon csak az SM kisebb SUC(3)´SUL(2)´UY(1) szimmetriája érvényesül.
A fermion anyagtereinket, ezek a kvarkok és a leptonok, nagyszerûen el tudjuk helyezni SU(5) multiplettekben. A legegyszerûbb 5 elemû ábrázolásban a felsõ három komponens az SUC(3) szín, míg az alsó kettõ a gyenge SUL(2) szerint transzformálódik a szimmetriasértés után. Így egy részecskeötösben lesznek kvarkok és leptonok. Nagy energián, az SU(5) szimmetrikus fázisban, nem tudjuk megkülönböztetni õket, egységesen leptokvarkokként jelennek meg (2. ábra). Az egy részecskeötösben lévõ kvarkok és leptonok össztöltésének nullának kell lennie, ezzel megvan a kapcsolat a különbözõ töltések között. 3*qd+qe+=0, azaz a d-kvark töltése –1/3. A GUT valóban megoldja a töltéskvantálást. Az elsõ család maradék ismert fermionjait is könnyen elhelyezhetjük a soron következõ legegyszerûbb, 10 dimenziós ábrázolásba (2. ábra mátrixa). Tehát egy család fermionjait teljes multiplettekbe tudjuk elhelyezni, úgy, hogy eddig ismeretlen új anyagrészecskéket nem kellett feltételezni. Az egyes multiplettekben lévõ részecskék tömege nagy energián megegyezik, ezért különösen nem kívánatos ismert részecskéket eddig ismeretlenekkel egy ábrázolásba tenni.
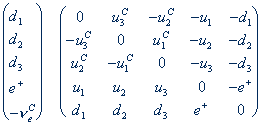
2. ábra. Kvarkok, leptonok az SU(5) GUT-ban, az u-, d-kvarkok 1, 2, 3 indexe a SUc(3) három színét, a C index a töltéskonjugált (anti-) részecskéket jelenti
Az egy multiplettbe került ismert kvarkok és leptonok tömege is egyenlõ nagy energián. Ezeket a tömegeket a mai ismert energiákra visszafuttatva – ugyanúgy, mint a csatolási állandókat, csak ellenkezõ irányba – egyes tömegarányok helyre tehetõk, de a d-kvark és az elektron tömegének aránya 15, ezt már nem lehet megmagyarázni. A következõ gond, hogy ugyanilyen multipletteket kell vennünk a maradék két családra is, tehát a három család megjelenését és a tömegspektrumot nem sikerült megmagyarázni.
Az SU(5) GUT-nak 24, kölcsönhatásokat közvetítõ mértékrészecskéje van. Remekül el tudjuk helyezni az ismert 8 gluont, a 3 gyenge vektorbozont és az UY(1) hipertöltés mértékbozonját is. A maradék 12 mértékbozon teljesen új, eddig ismeretlen kölcsönhatásokat közvetít. Közös multiplettbe rendeztünk kvarkokat és leptonokat, ezért nagy árat kell fizetnünk. Az új X, Y mértékbozonok leptonokat kvarkokba alakítanak át és fordítva, ezzel sértve a leptonszám és a barionszám megmaradását. Ezek a folyamatok már alacsony energián a proton elbomlásához vezetnek úgy, mint ahogy a W közvetíti a neutron b-bomlását. X, Y közvetítésével a proton pozitronra és semleges pionra bomolhat, míg a neutron pozitronra és negatív töltésû pionra. A proton élettartama arányos az X-bozon tömegének (MX) negyedik hatványával, azaz ha X, Y kellõen nehezek, akkor a bennünket is felépítõ proton nincs veszélyben.
A szimmetriák hierarchikus, egymást követõ sérülését egy 24 és egy 5 komponensû skalár térrel tudjuk leírni. Elõször az SU(5) szimmetria sérül az MX nagy egyesítési skálán és itt kapnak tömeget a leptonokat és a kvarkokat keverõ, sérült szimmetriákhoz tartozó mértékbozonok X, Y. Ezt a 24 komponensû skalár tér biztosítja, míg az 5 komponensû Higgs-tér 100 GeV-en sérti a gyenge SU(2) szimmetriát, és tömeget kapnak a W±-, Z0-bozonok.
SU(5) ® SU(3)C´ SU(2)W´ U(1)Y® SU(3)C ´ U(1)
Az elektrogyenge skálát mérésekbõl ismerjük már. A GUT, nagy egyesítési skálát, és X, Y tömegét, MX-t viszont meg tudjuk határozni 3 csatolási állandó futásából, amelyek 2·1015 GeV energián egymáshoz közel, de nem egy pontban találkoznak. Ennek eredményeként a legegyszerûbb SU(5) GUT legfeljebb néhányszor 1030 év élettartamot engedélyez a protonnak.
Az univerzum életkora 15 milliárd, azaz 1,5·1010 év, eddig nem sok proton bomolhatott el, de a kísérleti fizikusok elhatározták, hogy megfigyelik a proton bomlását. Egy proton 1030 év alatt bomlik el, de ha 10 000 tonna víz közel 1033 protonját figyeljük, akkor már évi 1000 protonbomlást várhatunk. A kísérletet védeni kellett a kozmikus sugárzástól, ezért a fizikusok a világ minden táján bányákban, alagutakban építettek nagy víztartályokat. Ezeket körbevették detektorokkal. Protonbomlásra utaló jeleket nem találtak, így megállapíthatták, hogy a proton élettartama legalább 1032 év, vagy akár végtelen is lehet. A minimális SU(5) ezzel elvesztette nagy vonzerejét, de számos más, bonyolultabb GUT-ot javasoltak az elméleti fizikusok, amelyekben a proton kellõen nagy élettartamú.
Sikeres-e igazából az SU(5) GUT?
Megmagyarázza a töltések kvantáltságát,
a gyenge kölcsönhatás fontos paraméterét,
a Weinberg-szöget is jól adja vissza és sikerült
nagyjából egyesíteni a 3 csatolási állandót.
Pontosabban megvizsgálva kiderül, hogy valamilyen új
részecskéknek fel kell bukkanniuk még az elektrogyenge
és a GUT-skála között, hogy a hármas találkozás
tökéletes legyen. Ezek származhatnak például
szuperszimmetrikus elméletekbõl. A GUT-okban továbbra
is sok az ad hoc módon beállított paraméter,
a proton élettartama túl rövid. A 3 család egyesítése
és megértése sem megoldott, a leírására
megpróbáltak bevezetni a családokat összekapcsoló
szimmetriákat, de ezek nem eredményesek. Az egyik legjelentõsebb
gond, a hierarchia probléma még mindig megoldásra
vár, hiszen a szimmetriasértést még mindig
védtelen skalárterekkel írjuk le.
Kitérõ a neutrínó nyomában
A föld mélyén dolgozó kísérleti fizikusok 1987-ben szokatlanul sok eseményt láttak, de nem protonbomlásból. Három független kísérlet is egy szupernóvarobbanásból érkezõ neutrínók keltette folyamatokat figyelt meg. Kiderült, hogy a neutrínók kiváltotta reakciók összhangban vannak a szupernóvakitörés modelljével, a proton továbbra sem bomlott el. Ekkor a protonbomlás vizsgálata közben a neutrínók, mint zavaró háttéresemény jelentkeztek.
A semleges neutrínó kölcsönhatásai nagyon gyengék, ezért szinte akadálytalanul halad át a bolygókon, vastag kõzetrétegeken is. Kis lépés volt rájönni arra, hogy még nagyobb víztartályokkal a Földünket az ûrbõl és a Napból is folyamatosan bombázó neutrínókat is elkaphatjuk. Ma már 50 000 tonna víz állja a neutrínók útját a japán Kamioka ólombányában és a fizikusok arra a kérdésre keresik a választ, hogy van-e tömege a neutrínónak. Ezekben az egyre nagyobb és nagyobb kísérletekben lassan a protonbomlás mint háttérzaj jelentkezhet. A neutrínók az SM kísérletileg azonosított részecskéi közül a legszemérmesebbek, nagyon gyenge kölcsönhatásaik miatt. Az SM-ben a neutrínók nulla tömegûek és a korábbi mérések mind csak felsõ korlátot adtak a neutrínó tömegére.
Az asztrofizikusok viszont már régóta szerették volna, hogy a neutrínónak legyen tömege, mert a könnyû kis részekbõl olyan sok található a világegyetemben, hogy egy csekély, néhány 10 eV-os tömeg már ideális sötétanyag-jelöltté emeli a neutrínót. Mi a sötét anyag? Az univerzumban látható, világító anyag nem elegendõ a világ tágulásának pontos leírásához. További nem látható, sötét anyagot kell feltételeznünk, amely például a jól ismert részecskékkel nem vagy csak nagyon gyengén hat kölcsön. A neutrínó kiváló jelölt. A föld alatti kísérletekben az utóbbi években azt tapasztalták, hogy a Napból érkezõ neutrínók váltogathatják a típusukat (ne, nm , nt), oszcillálnak. Ezt az elméletek csak a neutrínók közti tömegkülönbséggel, azaz tömeges neutrínóval tudják megmagyarázni.
A neutrínónak már az SM kis
megváltoztatásával tudtunk tömeget adni egy új,
jobbkezes szinglet nR tér
bevezetésével. Az SU(5) GUT-ban is egy ilyen extra teret
kell feltételeznünk, de a libikóka („see-saw”) mechanizmus
segítségével az ismert neutrínók tömege
természetesen kicsi lesz, míg az új, nem kívánt
tömeg a GUT-skálán marad. (Egyik fenn, másik
lenn.) Az SU(5)-nél nagyobb GUT-okban a nR
tér az ábrázolásokban természetesen
megjelenik, nem kell mesterségesen betennünk. A neutrínók
tömegarányai az egyszerû modellekben megegyeznek a velük
egy családban szereplõ kvarkok tömegarányával,
a mérések viszont nem ezt mutatják, a GUT-elméletek
ezen a téren is kiegészítésre szorulnak.
A hierarchia probléma megoldása
Ha egy fizikai mennyiség kis értéket vesz fel, akkor mindig egy szimmetriaelvet keresünk mögötte, amely a kis értéket biztosítja. A fermiontömegek a királis szimmetria miatt kicsik.
A kiralitás a jobbra (R) és balra (L) polarizáltan keletkezõ fermionok közt tesz különbséget. Ha a királis szimmetria egzakt volna, akkor a fermionoknak nulla volna a tömege. A kiralitás csak kevéssé sérül, így a fermionok tömege nem lehet az elektrogyenge skálánál jóval nagyobb. Ez lehet a megoldása a skalár tömeg stabilizálásának is, egy egészen új szimmetriát kell bevezetnünk. Ez a szuperszimmetria (SUSY), amely minden egész spinû részecskéhez egy azonos tömegû feles spinû szuperpartnert rendel és fordítva. Ekkor a pár fermionikus tagja könnyû lesz, mert védi a királis szimmetria, a bozonikus párja meg közel azonos tömegû a szuperszimmetria miatt. Technikailag a skalárok tömege azért maradhat kicsi, mert minden részecske és szuperpartnere pontosan ugyanakkora, de ellenkezõ elõjelû hurokkorrekciót ad a skalár tömeghez, amely így természetesen maradhat meg az eredetileg beállított értéken. Mivel ilyen azonos tömegû bozon-fermion párokat nem ismerünk, ezért minden szuperpartner egy-egy új részecskét jelent. Az új szimmetria leírása sem egyszerû, mert az eddigi 3 tér és 1 idõ bozonikus koordináta mellé is fel kell vennünk 4 új fermionikus módon viselkedõ koordinátát, ez adja a nyolcdimenziós szuperteret. A szuperszimmetria érdekessége még, hogy a hagyományos 4 dimenziós kvantumtérelméleti leírásban ez lehet az elmélet legtágabb típusú, legutolsó szimmetriája. A szuperszimmetria alapgondolata a húrelméletbõl származik, és nagy energián a szupergravitáció elméletében még a gravitáció és az SM kölcsönhatásainak az egyesítése is elképzelhetõ.
Az egyik legújabb javaslat szerint a hierarchia probléma megoldását extra térdimenziókban kell keresni. Az ismert világunkban ekkor csak a 100 GeV-es elektrogyenge energiától nem messze jelennek meg az újabb energiaskálák és nem itt kell megmagyaráznunk a nagy energiakülönbségeket.
Kis kitérõ a szimmetriákról. Az elméleti fizikusok két dologért képesek minden követ megmozgatni. Egyrészt, hogy egy elméletben új szimmetriát, rendezõ elvet találjanak, másrészt, hogy ezután az elmélet megoldásaiban (pl. a részecskék tömegeiben) kicsit sértsék ezt a szimmetriát. Ez a spontán szimmetriasértés. A tapasztalatok ugyanis általában közelítõ szimmetriákat mutatnak, például két részecske tömege közel egyenlõ. Skalár részecskéket feltételezve nagyvonalúan és gazdaságosan írhatjuk le a jelenséget, de az elméleti problémák ellenére is csak indirekt kísérleti eredmények támogatják. Ha természetben megfigyelt jelenségekkel akarjuk megmagyarázni a spontán szimmetriasértést, akkor jutunk el a dinamikai szimmetriasértés gondolatához.
A hierarchia probléma megoldásának
másik nagy útja a dinamikai szimmetriasértés,
amikor megszabadulunk az elemi skalárterektõl. Ezekben a
modellekben valamilyen aszimptotikusan szabad mérték-kölcsönhatás
az energia csökkenésével egyre erõsebbé
válik és egyes fermionok párokba rendezõdnek,
a kezdeti szimmetriát sértõ kondenzátumot
hoznak létre a vákuumban, és ez sérti valamelyik
nagy energián érvényes szimmetriát. Itt a kölcsönhatás
dinamikája vezet a sértéshez, szemben a Higgs-bozonos
módszerrel, ahol egy önkényesen választott statikus
potenciál origótól távol kerülõ
minimuma biztosítja ugyanezt. Amikor az egyre erõsebbé
váló csatolási állandó közel egységnyi
lesz, természetesen jelenik meg az elméletben egy új
energiaszint,
ahol sérül egy szimmetria. Nagy energián több különbözõképpen
erõsödõ kölcsönhatásból indulva
természetesen adódik több szimmetriasértési
skála. A csatolási állandók logaritmikus futása
miatt a szimmetriasértési szintek különbözõ
nagyságrendûek lehetnek. Ez a mechanizmus jelen van az elméletekben,
tehát nem kell mesterségesen kitalálnunk, szemben
azzal, hogy a skalár részecskék számára
önkényesen kell bevezetnünk speciális kölcsönhatásokat.
A dinamikai szimmetriasértés mellett szól még,
hogy a természetben mindeddig nem találtak semmilyen elemi
skalár részecskét és a spontán szimmetriasértést
elõször mutató jelenségért, a szupravezetésért
is fermion (eletron) pár felelõs. A következõkben
a hierarchia probléma mindkét megoldására konkrét
példákat láthatunk.
A minimális szuperszimmetrikus standard modell (MSSM)
Az MSSM alacsonyenergiás szuperszimmetrikus elmélet, az SM szuperszimmetrikus kiterjesztése, amelyben minden ismert részecskéhez egy szuperpartnert rendelünk hozzá. A leptonok és kvarkok párjai a nulla spinû (tehát skalár) szleptonok és szkvarkok. A mértékbozonok szuperpartnerei feles spinû gaugínók, részletesen a fotínó, wínó, zínó, gluínó, a Higgs-bozonok párjai a feles spinû higgszínók. Az MSSM-ben sok új részecskével kell megbirkóznunk.
Az MSSM-et a szimmetriák és a renormálhatóság feltétele a szuperpotenciál nevezetû rész kivételével teljesen meghatározzák. A szuperpotenciálba két- és háromrészecske kölcsönhatások kerülhetnek, melyek egy része az SM mintájára a részecskéknek tömeget ad. Megjelennek viszont barion- és leptonszámsértõ kölcsönhatások is, melyek a proton gyors elbomlásához vezetnének. Az SM-mel szemben, ahol a barion- és leptonszámsértõ folyamatok nem jelenhettek meg, a proton stabilitását az MSSM-ben egy új, R-paritás nevû szimmetria bevezetésével biztosíthatjuk. Minden ismert részecske R-paritása 1, míg a szuperpartnereké –1. Ezek után megköveteljük, hogy az elméletünk invariáns legyen az R-paritásra, csak olyan kölcsönhatások fordulhatnak elõ, amelyekben a részecskék R-paritásainak a szorzata +1-et ad. Az R-paritás mindvégig szimmetriája marad az elméletnek, ezért a szuperrészecskék csak párokban keletkezhetnek és a legkönnyebb stabil. Erre a tényre épül a szuperpartnerek keresésének legtöbb kísérleti módszere, és ha a legkönnyebb szuperrészecske stabil, akkor az ideális sötétanyag-jelölt.
Szuperszimmetrikus esetben a részecske és szuperpartnere pontosan egyenlõ tömegû, de eddig semmilyen kísérletben sem láttak szuperrészecskéket. Alacsony energián tehát a szuperszimmetria sérül, a párok tömegei eltérnek, de a szuperpartnerek legfeljebb 1-2000 GeV-es tömeget kapnak. A tömegkülönbség az ismert és a szuperrészecskék között azért nem lehet nagyobb, mert csak így tarthatják alacsonyan a Higgs-skalárbozonhoz számolt hurokkorrekciókat. Tehát a szuperszimmetriának sérülnie kell a jelenlegi kísérletek szintjén.
Kiderül, hogy a SUSY-t sokkal nehezebb sérteni, mint kiróni. Nem sérthetjük kezdetben direkt módon, mert akkor a jó hatásait elveszítenénk. Az elméleti fizikusok által elõnyben részesített spontán sértésnek két fõ útja is lehetséges, de egyik sem kielégítõ. Vagy nem kívánt, majdnem nulla tömegû részecskéket kapunk, amelyeket már rég látnunk kellett volna, vagy pedig a nagy egyesített modellel nem érvényesülhet együtt a SUSY. Helyettük puha, szoft SUSY-sértõ kölcsönhatásokat vezethetünk be (a puha jelzõ arra utal, hogy ezek nem hozzák vissza a hierarchia problémát). Emögött a következõ kép van: van egy távoli „rejtett” fizikai szektor, melyben a SUSY spontán sérül, ez az ismert elektrogyenge skálánál jóval nagyobb energiákon történik. A SUSY-sértést ezután valamilyen mechanizmus, gravitáció vagy akár az ismert mértékkölcsönhatások közvetítik az MSSM „látható” részecskéinek. A sértés és a közvetítés részleteit nem ismerve feltételezünk puha SUSY-sértõ kölcsönhatásokat, így a rejtett szektor skálája alatt érvényes effektív elméletet kapunk. Ezek a kölcsönhatások sok tömegtagot, két- és háromrészecske kölcsönhatást tartalmaznak. Általánosságban az MSSM csak a mértékcsatolási állandókban nevezhetõ minimálisnak, ugyanis további feltételek nélkül 124 szabad paramétert tartalmaz. Ismert fizikai érvekkel a paraméterek számát kicsit tudjuk csökkenteni, de még mindig túlságosan sok marad. A legnépszerûbb, szupergravitáció motiválta MSSM-ben a szoft SUSY-sértõ kölcsönhatások egységesek a Planck-skálán és csupán öt paraméterünk marad, melybõl kettõ a most következõ Higgs-szektorban van.
Az MSSM-ben már két Higgs-skalárdublettet kell elhelyeznünk, ez nyolc részecskét jelent. Kiderül, hogy az elektrogyenge szimmetriát csak kvantumeffektusok segítségével tudjuk sérteni. A nyolc Higgsbõl az SM mintájára hármat „megesznek” gyenge mértékbozonok, és ezáltal válnak tömegessé, és 5 fizikailag is megfigyelhetõ Higgs-skalárunk marad: 3 semleges, h, H, A és két töltött, H+, H–. A szuperszimmetria erõs megszorítást jelent a Higgs-szektorra is, a legkönnyebb semleges Higgs (h) tömege a Z-bozon tömegénél nem lehet lényegesen nagyobb, legfeljebb 135 GeV. A SUSY kísérleti kutatásának egyik nagyon fontos iránya a h részecske keresése, amely a jelen, vagy a közeljövõ gyorsítói elõl már nem bújhat el. Eddig nem látták a kísérletekben, ez alapján a tömegének legalább 90 GeV-nek kell lenni. Ha a gyorsítókban 140 GeV-ig kizárják a h létezését, akkor az MSSM-t le kell váltanunk egy összetettebb szuperszimmetrikus elméletre, de elképzelhetõ, hogy a fizikusok szuperszimmetriába vetett töretlen bizalma rendül meg, és más, esetleg dinamikai szimmetriasértési leírások kerülnek elõtérbe.
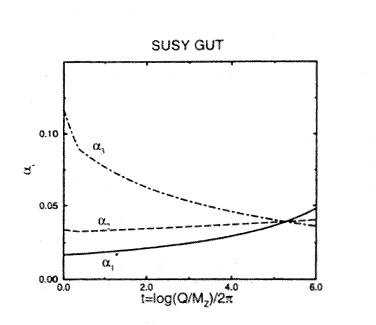
3. ábra. A három csatolási állandó változása, futása a kölcsönhatási energia függvényében a SUSY GUT-ban
Összegezzük az MSSM eredményeit!
Az MSSM nagyon vonzó elméleti ötletre, a szuperszimmetriára
épül, a hierarchia problémát semlegesíteni
tudja. Az elmélet rendkívül sok új részecskét
jósol, melyeknek a kísérletekben semmiféle
jelét sem látták eddig. Az MSSM mellett még
két indirekt tény szól. A szuperszimmetrikus nagy
egyesített elméletben a három mértékcsatolási
állandó valóban találkozik a GUT-energián
(3.
ábra), másrészt a proton élettartama összhangba
kerül a kísérletekkel. Mindennél jobban várunk
azonban bármilyen apró, de közvetlen kísérleti
megerõsítést.
Dinamikai szimmetriasértés
A mintát a kvantum-színdinamika alacsony energián tapasztalt viselkedése mutatja. A kvantum-színdinamika aszimptotikusan szabad elmélet, csökkenõ energián (növekvõ távolságon) a kölcsönhatás egyre erõsebbé válik. Ennek egyik rendkívül érdekes következménye a kvarkbezárás, nem tudunk megfigyelni szabad kvarkokat. Ugyanakkor a csökkenõ energiával egyre vonzóbbá váló erõs kölcsönhatás kvark-antikvark párokat kapcsol össze. Ezek a párok a vákuumban kikondenzálódnak, hasonlóan, mint a vízcseppek a vízgõzbõl, azzal a különbséggel, hogy a tér minden pontjában jelen vannak, megváltoztatják az „üres” vákuumot. A kvark és antikvark különbözõképpen viselkedik a gyenge SU(2), ill. a kiralitás szempontjából. A kvark–antikvark-párkondenzátum a vákuumban sérti a királis szimmetriát és a gyenge SU(2)-t, pontosan úgy, ahogy az SM-ben elvárjuk. Nagyon meglepõ dolog történt. Az egyre erõsebbé váló, a kvarkot és antikvarkot demokratikusan kezelõ erõs (szín) kölcsönhatás sértett egy olyan szelíden szemlélõdõ szimmetriát, amely különbözõképpen kezelte a kvarkot és az antikvarkot. Ez a kísérletileg is megerõsített királis szimmetriasértés. Kiderül, hogy a QCD tömeget tud adni a W±, Z gyenge mértékbozonoknak, de ez a p-mezonok 100 MeV körüli tömegének nagyságrendjébe esik (»30 MeV).
A felismerésbõl ragyogó ötlet született: legyen egy újfajta szín kölcsönhatásunk, a technicolor, amely 3000-szer nagyobb energiaskálán mûködik, mint a kvantum-színdinamika. Legyenek új fermionjaink is, a technikvarkok, amelyek SU(2) szempontjából ugyanúgy viselkednek, mint a kvarkok. A kölcsönhatás a technikvarkot párba kényszeríti az antirészecskéjével és ezzel sérti a gyenge SU(2)-t és pontosan 80 és 90 GeV-es tömeget ad a W±, Z-bozonnak. Ez a technicolor elmélet azonban elvérzett a további ellenõrzéseken. A nagy energián megismételt, felskálázott erõs kölcsönhatás magával hozta az összes részecskéjét is. A technicolor-elméletben megjelennek a technimezonok és technibarionok, amelyeket a kísérletekben nem láttunk még. Még nagyobb problémát jelent, hogy a fermionokat is tömeggel kell ellátni. Ez csak még újabb kölcsönhatások feltételezésével, a kiterjesztett technicolor-elméletben lehetséges. A legnehezebb top kvarknak csak olyan áron tudunk tömeget adni, ha a kiterjesztett technicolor-elmélet már 500 GeV-en érezteti hatását. Az elmélet ekkor viszont olyan kölcsönhatásokat eredményez, mintha egy furcsán viselkedõ új semleges Z*-bozonunk lenne, amely összekeveri a kvarkízeket, családokat. A kísérletek nagyon érzékenyen mutatják, hogy márpedig ilyen kölcsönhatások nincsenek, a technicolor-elmélet halott.
A kitartó elméleti fizikusok újabb és újabb módosításokkal próbálkoztak mindaddig, amíg a Z-bozon tulajdonságainak mérései el nem érték az egy százalék pontosságot. Ekkor már az elmélethez számolt kvantumos hurokkorrekciók a mérésekkel ellenkezõ irányba mutattak. Ezzel a holt elmélet még egy kegyelemdöfést kapott és végleg kimúlt. Néhány még szívósabb fizikus újabb ötlettel állt elõ. A sétáló technicolor-elméletben a csatolási állandó annyival lassabban fut, mint a kvantum-színdinamikában, hogy már sétál. Ezzel az elsõ két probléma megoldható, a hurokkorrekciók ideig-óráig összhangba kerültek az elmélettel.
A következõ nagyszerû javaslat kész anyagból építkezett. Az SM-bõl nagy tömege miatt kilógó nehéz top kvark inspirálta a fizikusokat, hogy a topot külön kezeljék. Feltételezték, hogy a top részt vesz egy nagyon vonzó kölcsönhatásban, top-antitop párok alakulnak ki a vákuumban és ez sérti a szimmetriát. Ez a top kondenzátum modell nem jósolt sok új részecskét, veszélyes kölcsönhatásokat, de kiderült, hogy alacsony energián megkülönböztethetetlen a skalárrészecskéket tartalmazó SM-tõl, nagyobb energián meg nem maradtak meg a vonzó tulajdonságai.
Magyar csoport javasolt egy új modellt. Ebben nem fermionok, hanem 1-spinû nehéz bozonok alkotta kondezátum sérti a gyenge szimmetriát. Az elmélet véges energiáig érvényes, a sugárzási korrekciók jelentõsen megszorítják az új részecskék lehetséges tömegét, de azok a gyorsítók következõ nemzedékében felbukkanhatnak. Ez a javaslat megmutatta, hogy a standard Higgs-skalárrészecskét tartalmazó modellek mellett más effektív leírás is érvényes lehet.
Az SM felbecsülhetetlen sikerei ellenére elméleti és kísérleti fizikusok fáradoznak azon, hogy megtalálják azt az elméletet, amely az SM-et követi, mert a tények meggyõzõek, hogy új természeti jelenségek várnak ránk kicsit nagyobb energiákon a közeli jövõben, legkésõbb az LHC gyorsítón.
Irodalom
[1] Harald Fritzsch: Kvarkok, Gondolat, Budapest,
1987.
[2] Leon Lederman: Az isteni a-tom, Typotex,
Budapest, 1995.
 CYNOLTER
GÁBOR (1969), PhD, tudományos fõmunkatárs,
az MTA ELTE Elméleti Fizikai Tanszéki Kutatócsoportjában.
A Fazekas Mihály Gimnáziumban érettségizett
matematika tagozatos osztályban, majd fizikusdiplomát követõen
1998-ban védte meg PhD-jét az ELTE-n. 1999-tõl Bolyai
kutatási ösztöndíjas. Fõ kutatási
területe a részecskefizikai jelenségek, elektrogyenge
szimmetriasértés, Higgs-részecskék, szuperszimmetria. CYNOLTER
GÁBOR (1969), PhD, tudományos fõmunkatárs,
az MTA ELTE Elméleti Fizikai Tanszéki Kutatócsoportjában.
A Fazekas Mihály Gimnáziumban érettségizett
matematika tagozatos osztályban, majd fizikusdiplomát követõen
1998-ban védte meg PhD-jét az ELTE-n. 1999-tõl Bolyai
kutatási ösztöndíjas. Fõ kutatási
területe a részecskefizikai jelenségek, elektrogyenge
szimmetriasértés, Higgs-részecskék, szuperszimmetria. |
| Természet Világa, | 2000. III. különszám
http://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez