BAY ZOLTÁN
A foton.
Elôzô rész
Fölmerült a kérdés, mi történik
a fotonnal, a foton energiájával, ha a hullámot különbözô
módokon befolyásoljuk.
Ismeretes a régebbi interferencia-kísérletekbôl,
hogy a fénysugárzás a tovaterjedés irányában
véges hosszúságú hullámsorból,
hullámvonulatból áll. Ha egy interferencia-kísérletben
az útkülönbséget egyre növeljük, akkor
az interferencia egy az illetô fénynemre jellemzô útkülönbségen
túl megszûnik. Ez az útkülönbség éppen
a hullámsor hossza. Ez alapon a fénykibocsátás
lefolyására a következô átlagos képet
nyerjük.
Egy atom kisugárzása 1 százmilliomod mp. nagyságrendû
ideig tart; ez mégfelel zöld fény esetében kb.
1 millió teljes rezgésnek. Ez idô alatt a hullámfront
kb 1 méter utat tett meg, tehát az atomból kijövô
hullámzás egy egyre jobban kiterjedô gömbhéjat
tölt meg, melynek vastagsága kb 1 méter. Ebben a gömbhéjban
történhetik meg valahol a foton energiaátadási
jelensége, mely szinte pontszerûen nyilvánul, pillanatnyilag,
míg a hullámsor kiterjedés térben és
idôben véges. Az egyszerû elképzelés azt
mondaná, hogy a foton valahol ebben a térrészben “utazik”.
Rekesszük ki ennek a hullámsornak egy részét
azáltal, hogy ernyôt helyezünik a hullám útjába,
melyen nyílás van. Akkor a gömbhéjból
“hurkát” csináltunk. Ezt a hurkát elmetszhetjük
keresztirányban is, úgy, hogy olyan “pillanatzárat”
alkalmazunk, amelyet százmilliomod mp-nél kisebb ideig tartunk
nyitva, és így a hurka nem mehet át rajta egész
hosszában (Kerr-cellával ilyen rövid pillanatzár
megoldható), vagy pedig kettéoszthatjuk törés
és visszaverôdés által, midôn egyik hurka
a megtört, másik a visszavert sugárban halad.
Mi történik a fotonnal a hullámtér ilyen feldarabolása
esetében?
Ramsauer, Bothe, Rupp és mások kísérletei
– melyekre itt nem terjeszkedhetünk ki –, megmutatták, hogy
a foton energiáját ilyen feldarabolásokkal nem tudjuk
feldarabolni, hanem a foton energiája mindig egységesen jelentikezik,
a feldarabolt térrészek valamelyikében, látszólag
a nélkül, hogy a hullámtér feldarabolása
bármennyire is befolyásolta volna a fotont. Ez a kijelentés
azonban még finomabb megvizsgálásra szorul.
Tovább vitte a gondolatmenetet Einstein, aki a “hurkát”
sok részre bontotta fel. Az általa javasalt kísérletben,
melyet Rupp végzett el, világító csôsugár-ionok
nagy sebességgel haladnak el egy optikai rács mögött,
a rácsvonalakra merôlegesen. A rácsvonalak a fényt
eltakarják, míg a rácsvonalak között a fény
átjut, a hurka tehát annyi darabra "vágódik"
szét, amennyi rácsvonal van. A kísérletbôl
kétféle eredményt várhatunk.
1. Az atom a fénykvantumot momentán, pillanatszerûen
emittálja. Így az egész energia valamelyik rácsközön
jut át és frekvenciaváltozás nélkül
észleljük a fotont. A hullámsor többi része
hatástalan marad, tehát hatástalan a feldarabolás
is.
2. A hullámsort sûrû feldarabolással megváltoztattuk
– olyan érteIemben, mint az antenna kisugárzását
a rádióban a beszéd frekvenciája szerint való
kivezérléssel – azaz moduláltuk. A moduláció
azt eredményezi a hullámtan szerint, hogy a vivôfrekvencia
(jelen esetben a fény rezgésszáma) mellett megjelenik
a két odalfrekvencia, melyek a moduláció frekvenciájának
a vivôfrekvenciához való hozzáadásával
ill. levonásával keletkeznek. Változás történt
tehát a fény színében.
Rupp kísérlete a 2. eredményt adta: kimutatható
volt a fény rezgésszámváltozása.
A kísérletet késôbb Rupp közvetlen idôbeli
modulálással is végrehajtotta. E célra a fényt
Kerr-cellán engedte át, melynek elektródjait 1000
megaciklus frekvenciájú (l = 30
centiméteres rádióhullámok) elektromos rezgéssel
táplálta. Az eredeti higany-rezonanciavonalnak a két
oldalfrekvenciára való felhasadását
sikerült kimutatnia.
Az Einstein-Rupp kísérletekbôl nyilvánvaló,
hogy a foton és a hullám között szoros kapcsolat
van, a hullám befolyásolása visszahat a fotonra s
a fény rezgéselméletébôl levonható
következtetések érvénnyel bírnak a foton
viselkedésére nézve. Nem kereshetünk tehát
alternatívát a fény korpuszkuláris vagy
hullámelméleti magyarázatában, hanem a
fényjelenségek megértésénél és
leírásánál az alternatíva mindkét
oldalára szükségünk van. Az új fényelmélet
csakis a hullám–korpuszkula tulajdonságok valamilyen szintézise
lehet.
Ennek a szintézisnek a véghezvitelére (elteikintve
az egyes kutatók részletmegoldásaitól) lényegébn
véve három átfogó elgondolás történt,
melyek közül a harmadik bizonyult megfelelônek.
1. Bohr, Kramers és Slater (1924) szerint a vákuumban
mozgó fotonok, melyekben az energiát összpontosítva
gondoljuk, nem reálisak. A valóságban fotonokat sohasem
figyelünk meg, hanem megfigyeljük az atomokon végbemenô
folyamatokat: emissziót, abszorpciót, szórást
stb. A sugárzási mezô, azaz a fényhullám,
szintén virtuális, s az atomok között létesít
bizonyos kapcsolatot, mely valószínûségi jellegû.
Ha tehát pl. fényt kibocsátó atom van jelen,
akkor meg lesz a valószínûsége annak, hogy valahol,
ahol azt a virtuális hullámtér meghatározza
(ez természetesen kiterjedt térrész) abszorpciós
aktus menjen végbe (esetleg több atomon is). Az elemi aktusok
tehát csupán statisztikusan vannak egymáshoz kapcsolva,
így az egyes jelenségekre nem érvényes az energia
(és impulzus) megmaradásának elve sem, mert pl. miután
már egy atom emittált (energiája megkisebbedett),
de abszorpció még nem következett be, az energia hiányzik
a térbôl. Az sem bizonyos, hogy az emisszió aktusa
idôben elôtte jár az abszorpció aktusának.
A nagy számok törvénye gondoskodik arról, hogy
nagyban, makroszkopikusan az energia és impulzus megmaradása
érvényes marad, kicsinyben, a mikrokozmoszban azonban ez
nem állítató.
Elvileg ez az elmélet nern tartalmaz önellentmondást;
kérdés azonban, hogy a természet így viselkedik-e?
A modern kísérletezô technika megengedte ennek az
elméletnek megvizsgálását a mikrokozmoszban,
tehát atomi jelenségeken. Bothe és Geiger
1925-ben csúcsszámlálókkal kimutatták,
hogy Compton-effektusnál a szórt foton és a kiváltott
elektron egyidejûleg lépnek fel (koincidálnak),
tehát nem statisztikusan vannak összekapcsolva. Ez megcáfolja
Bohr, Kramers és Slater elgondolását.
Ugyancsak cáfolja ezt az elméletet Bothe egy másik
kísérlete, mely azt mutatja, hogy egy emissziós aktusra
csupán egy abszorpciós aktus következhetik, sohasem
több, másszóval: egy hullámsorban (gömbhéjban)
csupán egy foton "van jelen", ami ismét az energia-elv
érvényét jelenti kicsinyben is. Bothe ezt a kísérletet
röntgen-sugarakkal végezte s mindeddig hiányzik e kísérlet
elvégzése látható fénnyel. Láthartó
fotonok számlálása azok kicsiny energiája miatt
ezideig nehézségbe ütközött. E sorok írója
kidolgozott egy új eljárást, mely a látható
fény fotonjainak számlálására is alkamas
(elektronsokszorozó), s jelenleg különbözô
kísérletek vannak folyamatban e kérdésnek a
látható fény optikájában való
megvizsgálására.
Az eddigi kísérletek szerint tehát azt kell mondanunk,
hogy a természet nem úgy viselkedik, mint ahogy azt Bohr,
Kramers és Slater elmélete állitja.
2. Born elmélete (1925) már figyelembe veszi Bothe
és Geiger eredményeit is és az energia elvét,
s a fényjelenséget úgy képzeli, hogy az atom
ténylegesen emittálja a fotont, mely az emisszió egész
hn energiáját magával
viszi, de a foton mozgását a térben a hullámmezô
írja elô. Az az elôírás statisztikus,
valószínûségi jellegû, tehát a
fényhullámok itt is valószínûségi
hullámok. Végeredményben a foton úgy mozog,
hogy valamely térelembe való eljutásának, tehát
ott-találásának valószínûsége
az ottani hullámamplitudó négyzetével arányos.
Ez az elgondolás közel áll a végleges megoldáshoz,
mégsem tartható fenn. Nem érthetô pl., hogy
a foton hogyan megy át egy interferencia-kísérlet
sötét helyein, melyek mögött világos helyek
vannak. Így pl. álló fényhullámoknál
sötét és világos interferenciacsíkok váltogatják
egymást, s a sötét helyeken, csomósíkokban
a fotont nem észleljük, míg a közbeesô világos
helyeken igen.
Born elméleténak hibája abban áll, hogy
a fotonnak az interferencia-kísérletben pályát
tulajdonít. Máskülönben a ténylegesen megfigyelhetô
jelenségeket jól adja vissza, mert a klasszikus fényelmélet
fényintenzitását helyettesíti a foton megtalásának
valószínûségével. A klasszikus fényelmélet
a fény energiájának az egész hullámtérre
való szétosztását képzeli s az energiának
folytonos áramlását, ezt azonban kísérleteink
sohasem mutatják, mert minden energiamérés a foton
egész energiáját mutatja hn
mennyiségben. Hibás tehát a klasszikus
fényelmélet, midôn olyat állít, amit
nem figyelhetünk meg: az energia szétosztását,
s hibázik Born elgondolása, midôn szintén olyat
állít, amit nem figyelhetünk meg: a foton pályáját
az interférencia-jelenség közben.
3. Ez a kritikai meggondolás vezette Heisenberget és
tôle függetlenül Bohrt (1927) arra, hogy megtalálják
a fény korpuszkuláris és hullámtulajdonságainak
összeegyeztetési lehetôségét.
Ragaszkodjunk a tapasztalati ismeretelmélet álláspontjához:
a fizika csak olyan jelenségekkel foglalkozzék, melyek észlelhetôk.
A fizika története folyamán sokszor kisegítette
ez az elv a tudományt a nehézségekbôl. Elég,
ha Galileire utalunk, aki az akkori, elôitéletekkel telt gondolkozás
helyébe a megfigyelést és kísérletet
vezette be, vagy az Einstein-féle relaitivitáselméletre,
mely kiküszöbölte az abszolút, a jelenségektôl
független tér fogalmát.
 Heisenberg
és Bohr rámutattak arra, hogy a fény hullám-
s korpuszkula-jelenségei nincsenek egymással ellentmondásban,
mert nem jelentkeznek egyszerre. Végezhetünk a fénnyel
olyan kísérleteket, melyek annak korpuszkuláris tulajdonságát
mutatják (Compton-effektus, fotoeffektus, abszorpció stb.)
s ugyancsak végezhetünk olyanokat, melyek hullámtermészetét
tárják fel (interferencia), de ha az egyik féle kísérletet
végezzük, akkor elvész a lehetôsége annak,
hogy egyidejûleg a fény másik sajátságát
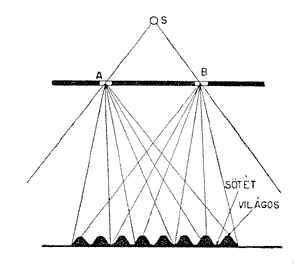
is vizsgáljuk. Így pl. az 1. képen bemutatott interferencia-kísérletet
berendezhetjük úgy, hogy pl. A nyílásnál
megállapíthatjuk a foton ott-tartózkodását
fényelektromos effektussal (fotonszámláló),
de ezzel teljesen megmásítottuk a kísérletet,
s az ernyôn nem kapunk inyerferenciacsíkokat, mert elfogyasztottuk
a foton energiáját. (Durván szólva: elfogtuk
az A nyílást s ezáltal elrontottuk az interferenciát.)
Ha pedig hagyjuk az interferencia-jelenséget zavartalanul végbemenni,
akkor nem ismeretes elôttünk – hiányzik a tapasztalásunkból
– olyan kísérlet, mely egyidejûleg megmutatná,
hogy a foton melyik nyíláson "jött keresztül".
Mivel pedig nem ismerünk ilyen kísérletet (ismételjük:
minden kísérlet, melyet e célból végzünk,
elrontaná az interferencia-jelenséget), nem is szabad feltételeznünk,
hogy a fotonnak közben pályája volt ugyan, csak mi nem
ismerjük. Mert olyan természeti jelenség, amit eIvileg
nem ismerhetünk, számunkra nem létezik, de ami számunkra
nem létezik, az nincs.
Heisenberg
és Bohr rámutattak arra, hogy a fény hullám-
s korpuszkula-jelenségei nincsenek egymással ellentmondásban,
mert nem jelentkeznek egyszerre. Végezhetünk a fénnyel
olyan kísérleteket, melyek annak korpuszkuláris tulajdonságát
mutatják (Compton-effektus, fotoeffektus, abszorpció stb.)
s ugyancsak végezhetünk olyanokat, melyek hullámtermészetét
tárják fel (interferencia), de ha az egyik féle kísérletet
végezzük, akkor elvész a lehetôsége annak,
hogy egyidejûleg a fény másik sajátságát
is vizsgáljuk. Így pl. az 1. képen bemutatott interferencia-kísérletet
berendezhetjük úgy, hogy pl. A nyílásnál
megállapíthatjuk a foton ott-tartózkodását
fényelektromos effektussal (fotonszámláló),
de ezzel teljesen megmásítottuk a kísérletet,
s az ernyôn nem kapunk inyerferenciacsíkokat, mert elfogyasztottuk
a foton energiáját. (Durván szólva: elfogtuk
az A nyílást s ezáltal elrontottuk az interferenciát.)
Ha pedig hagyjuk az interferencia-jelenséget zavartalanul végbemenni,
akkor nem ismeretes elôttünk – hiányzik a tapasztalásunkból
– olyan kísérlet, mely egyidejûleg megmutatná,
hogy a foton melyik nyíláson "jött keresztül".
Mivel pedig nem ismerünk ilyen kísérletet (ismételjük:
minden kísérlet, melyet e célból végzünk,
elrontaná az interferencia-jelenséget), nem is szabad feltételeznünk,
hogy a fotonnak közben pályája volt ugyan, csak mi nem
ismerjük. Mert olyan természeti jelenség, amit eIvileg
nem ismerhetünk, számunkra nem létezik, de ami számunkra
nem létezik, az nincs.
Összefügg mindez azzal a ténnyel, hogy megfigyelésünk,
mérésünk szükségképen beavatkozást
jelent a jelenségbe: a mérés befolyásolja a
mérendôt. A klasszikus fizika szerint, hol a mennyiségek
folytonosak, ez a beavatkozás a mérés gondos kivitelével
akármilyen kicsiny lehet, nem úgy azonban a kvantumfizika
szerint, hol pl. a “látás", a "megnézése
valaminek" nem mehet végbe kisebb energiával; mint egy
foton energiája.
Heisenberg kihangsúlyozta a mérésnek a mérendôre
való ellenôrizhetetlen behatását és ez
alapon véghezvitt szigorú kritikai meggondolásaival
feláIlította a róla elnevezett határozatlansági
relációkat. Ezekre nem térünk itt ki, csupán
megemlítjük, hogy ezek segítségével a
fénynek hullám- és korpuszkula-sajátsága
matematikailag is ellentmondásmentesen letárgyalható.
A legújabbkori fizika legnagyobb élményei közé
tartozik, hogy a fénynek ez a hullám–korpuszkula dualizmusa
az anyagra is érvényes. De
Broglie elméletileg jutott el az anyaghullámok gondolatára
1924-ben s Davisson és Germer 1927-ben kísérletileg
is igazolta kristályrácsokon az elektronok interferenciáját,
mely a fény interferenciájához teljesen hasonlóan
folyik le. Így a hullám–korpuszkula dualizmus a természetnek
megnyilvánulása, általános sajátsága.
Rá kell még mutatnunk arra, hogy mindezek a meggondolások,
melyekkel itt foglalkoztunk, az egy-foton problémájára
vonatkoznak. Természetesem új elméleti fizikai feladatok
merülnek fel, midôn feI akarjuk építeni a makroszkópikus
jelenségek sok-foton problémáját. Így
a kvantummechanika többtest-problémájának feladatkörébe
jutunk, melyet fotonoknál ugyanúgy meg kell oldani, mint
az anyagi részecskék esetében. Nem lehet célunk
itt ezekkel a kérdésekkel foglalkozni – ezek még nincsenek
is lezárva –, csupán azt jegyezzük meg, hogy a feladat
tulajdonképen a makroszkopikus elektromágneses hullámok
levezetése az új fotonelméletbôl, melynek alapelveit
itt ismertettük. Mert a dolgok következetes végiggondolása
azt mutatja, hogy az a hullám, melyre a korpuszkulával való
dualizmusáróI itt szó volt, még nem az elektromágeses
hullám, hanem a fotonnak az anyaghulláma vagy De Broglie-hulláma.
Az észleléseknek hozzáférhetô elektromágneses
hullám a sok-foton probléma anyaghullámából
származtatandó le, és ezen a téren még
az elméleti fizikának részletfeladatokba kell elmélyednie.
Hangsúlyozzuk még egyszer, hogy a modern fizika a hullám–korpuszkula
dualizmus megoldásakor nem ellentmondásokat egyesít,
hanem ellentmondásokat szüntet meg.
Bohr a hullám- és korpuszkula-sajátságokat
komplementereknek nevezte. Általában komplementerek
egy fizikai történésben szereplô azon mennyiségek,
melyek a hátározatlansági relációk értelmében
nem határozhatók meg egyidejûleg pontosan. Egyiknek
pontos meghatározása a másiknak teljes határozatlanságát
vonja maga után. A hullám és korpuszkula is, mint
komplementer jelenségek, egyidejûleg kizárják
egymást, de jól megférnek egymás mellett, ha
nem egyidejûleg jelentkeznek.
Az ember tehát megoldotta a természet által föladott
legnehezebb találós kérdést, de csupán
egész gondolkodásának gyökeres kritikájával.
Fel kellett adnunk mindennapos szemléletünk egyes elemeit,
mint pl. a pálya fogalmát az interferencia-kísérletben.
Ugyancsak föl kellett adnunk a kauzalitás elvét, mert
a fényhullámot csupán mint valószínûségi
hullámot tekinthetjük, mely nem determinálja a foton
megtalálásának helyét. De lássuk be,
hogy sem a minden áron megkövetelendô szemléletességet,
sem az okság elvét nem merítettük a tapasztalatból.
Nem vesztettük el tehát a csatát a természettel
szemben, hanem éppen megnyertük, mert a természetbôl
nyert új tapasztalatokat ellentmondásmentes logikai rendszerbe
tudtuk beilleszteni.
A nagy tanulság pedig az, hogy a természet még
a legegyszerûbb jelenségeiben is kimeríthetetlen, mindig
új és új oldaláról mutatkozik meg. A
fényrôl is biztosra vehetjük, hogy még sok új
tulajdonságát fogjuk megismerni, olyanokat, melyek kívül
esnek mai legmodernebb fényelméleteink keretein is. A feladat
akkor is az lesz, hogy változtassuk meg az elméletet, mert
a természetet nem tudjuk megváltoztatni, sem "gúzsba
kötni". Az emberi gondolkozásban pedig alig képzelhetô
el nagyobb hiba, mint egy elméletrôl az állítani,
hogy végleges.
| Természettudomány, |
III. évfolyam. 1948. 97–108. oldal
https://www.kfki.hu/chemonet/TermVil/
https://www.ch.bme.hu/chemonet/TermVil/ |
Vissza
 Heisenberg
és Bohr rámutattak arra, hogy a fény hullám-
s korpuszkula-jelenségei nincsenek egymással ellentmondásban,
mert nem jelentkeznek egyszerre. Végezhetünk a fénnyel
olyan kísérleteket, melyek annak korpuszkuláris tulajdonságát
mutatják (Compton-effektus, fotoeffektus, abszorpció stb.)
s ugyancsak végezhetünk olyanokat, melyek hullámtermészetét
tárják fel (interferencia), de ha az egyik féle kísérletet
végezzük, akkor elvész a lehetôsége annak,
hogy egyidejûleg a fény másik sajátságát
is vizsgáljuk. Így pl. az 1. képen bemutatott interferencia-kísérletet
berendezhetjük úgy, hogy pl. A nyílásnál
megállapíthatjuk a foton ott-tartózkodását
fényelektromos effektussal (fotonszámláló),
de ezzel teljesen megmásítottuk a kísérletet,
s az ernyôn nem kapunk inyerferenciacsíkokat, mert elfogyasztottuk
a foton energiáját. (Durván szólva: elfogtuk
az A nyílást s ezáltal elrontottuk az interferenciát.)
Ha pedig hagyjuk az interferencia-jelenséget zavartalanul végbemenni,
akkor nem ismeretes elôttünk – hiányzik a tapasztalásunkból
– olyan kísérlet, mely egyidejûleg megmutatná,
hogy a foton melyik nyíláson "jött keresztül".
Mivel pedig nem ismerünk ilyen kísérletet (ismételjük:
minden kísérlet, melyet e célból végzünk,
elrontaná az interferencia-jelenséget), nem is szabad feltételeznünk,
hogy a fotonnak közben pályája volt ugyan, csak mi nem
ismerjük. Mert olyan természeti jelenség, amit eIvileg
nem ismerhetünk, számunkra nem létezik, de ami számunkra
nem létezik, az nincs.
Heisenberg
és Bohr rámutattak arra, hogy a fény hullám-
s korpuszkula-jelenségei nincsenek egymással ellentmondásban,
mert nem jelentkeznek egyszerre. Végezhetünk a fénnyel
olyan kísérleteket, melyek annak korpuszkuláris tulajdonságát
mutatják (Compton-effektus, fotoeffektus, abszorpció stb.)
s ugyancsak végezhetünk olyanokat, melyek hullámtermészetét
tárják fel (interferencia), de ha az egyik féle kísérletet
végezzük, akkor elvész a lehetôsége annak,
hogy egyidejûleg a fény másik sajátságát
is vizsgáljuk. Így pl. az 1. képen bemutatott interferencia-kísérletet
berendezhetjük úgy, hogy pl. A nyílásnál
megállapíthatjuk a foton ott-tartózkodását
fényelektromos effektussal (fotonszámláló),
de ezzel teljesen megmásítottuk a kísérletet,
s az ernyôn nem kapunk inyerferenciacsíkokat, mert elfogyasztottuk
a foton energiáját. (Durván szólva: elfogtuk
az A nyílást s ezáltal elrontottuk az interferenciát.)
Ha pedig hagyjuk az interferencia-jelenséget zavartalanul végbemenni,
akkor nem ismeretes elôttünk – hiányzik a tapasztalásunkból
– olyan kísérlet, mely egyidejûleg megmutatná,
hogy a foton melyik nyíláson "jött keresztül".
Mivel pedig nem ismerünk ilyen kísérletet (ismételjük:
minden kísérlet, melyet e célból végzünk,
elrontaná az interferencia-jelenséget), nem is szabad feltételeznünk,
hogy a fotonnak közben pályája volt ugyan, csak mi nem
ismerjük. Mert olyan természeti jelenség, amit eIvileg
nem ismerhetünk, számunkra nem létezik, de ami számunkra
nem létezik, az nincs.