SELÉNYI PÁL
A katódsugarak nyomásának kísérleti kimutatása.
Kereken ötven éve tudjuk fôleg Thomson J. J. vizsgálataiból , hogy a katódsugarak villamos és mágneses térben negatív villamostöltésû, de egyúttal anyagi tömeggel, tehetetlenséggel is felruházott részecskék módjára mozognak, sôt az elektromos és mágneses eltérítés mértékébôl a töltés és tömeg viszonya (e/m = 1,76 · 108 coul/g) is kiszámítható; mégis minden arra irányuló kísérlet, hogy az elektronok anyagi tömégét, tehetetlenségét közvetlenül, mechanikai hatásaiból mutassák ki, a közelmultig eredménytelenül végzôdött. Pedig az erre irányuló törekvés olyan régi, mint maguknak a sugaraknak ismerete. Hiszen a Crookes-féle klasszikus katódsugárcsövek között, amint azok fizikai szertárainkban ma is, immár háromnegyed évszázad óta változatlan alakban fellelhetôk, kettô is van, mellyel szerzôjük a sugarak mechanikai hatását vélte kimutatni. Az egyik, a közismert "malomkerék-csô" amelyben csillámlemezkékbôl szerkesztett, vízszintes tengelyû kis "malomkerék" jobbra vagy balra forog, a szerint, hogy a katódsugarak a kerék alsó vagy felsô lapátjait érik , annak a nyomásnak a kimutatására szolgálna, amit a sugarak az útjukba helyezett akadályra fejtenek ki A másik, a talán kevésbbé elterjedt "katódsugár-radiométer-csô" hasonló szerkezetû; mint az ugyancsak Crookes-tól eredô közismert "fényradiométer amelynek titokzatos, szüntelen forgása a pesti optikusok kirakatában valaha sok érdeklôdô figyelmét vonta magára , mégis avval a különbséggel, hogy ebben a csôben a fémlapátocskák egyik oldala nem korommal van bevonva, mint a "fényi-malomban, hanem csillám borítja, a lapátos kerék fémtengelye áramhozzávezetéssel van ellátva és a maga egészében katódul szolgál, míg az anód, a csôben valahol lent, oldalt van elhelyezve. Ha a csövet villamos géppel vagy szikrainduktorral mûködésbe hozzuk, a lapátoknak csillámmal be nem borított oldaláról katódsugarak indulnak ki, s a kerék a sugarakkal ellenkezô irányú gyors forgásba jön, látszólag a sugarak kilépésekor fellépô visszaható erôt bizonyítván.
Miként azonban már régen ismeretes, hogy a "fényi-malmot" nem a fény nyomása, ez a rendkívül kicsiny erô, hanem a lapátok egyoldalú felmelegedésébôl származó és ennél sakszorosan nagyobb ú. n. radiométer-erôk hozzák forgásba, vagyis azok a taszító erôk, amelyek két különbözô hômérsékletû test között kis nyomású gázban azon okból lépnek fel, mert a két testrôl a molekulák különbözô sebességgel pattannak vissza, ugyanúgy tudjuk azt is, hogy ebben a kétféle katódsugár-csôben is a kerekek forgását nem a katódsugarak nyomása, illetve visszahatása, hanem ugyancsak a lapátocskák egyoldalú felmelegedésébôl eredô radiométer-erôk okozzák. Ezt az állítást a második csövön igen egyszerû kísérlettel, kétségbe nem vonhatóan be is bizonyíthatjuk. Ha ugyanis a mûködésben levô csôrôl az áramforrást lekapcsoljuk, vagyis a katódsugarakat megszüntetjük és a csövet kissé megbillentjük, akkor a lapátoskerék a fellépô tengelysúrlódás folytán megáll, de tüstént újra forgásnak ered, ha a csövet rövid idô multán talpára állítva, újra függôleges helyzetbe hozzuk. Nyilvánvaló, hogy a kerék forgását, most, mikor a csövön még villamos feszültség sincsen, csakis az elôbbi mûködése alatt létrejött és még ki nem egyenlített hômérsékleti különbségekbôl eredô radiométer-erôk okozhatják.
Egyébként az itt tárgyalt Crookes-féle kísérlet pontos értelmezése korántsem olyan egyszerû. A kísérlet ugyanis azon a hallgatólagos feltevésen alapul, hogy ha egy csôben például 50000 voltos sugarakat hozunk létre, akkor a katódra 50000 volt sebességû elektronok visszahatása mûködik. Ez azonban nincs így! Az elektronok egy testbôl (a katódból) mindig csupán a hômérsékleti energiájukból származó igen csekély sebességgel lépnek ki. Az ismeretes e · U = k · T egyenletbôl ahol e az elektron töltése, U a volt-sebessége" (az a fékezô feszültség, voltban kifejezve, amelyet sebességénél fogva le tud küzdeni), k a Boltzmann-féle állandó és T a test hômérséklete Kelvin-fokokban (vagyis a test abszolút hômérséklete) kiszámítható, hogy U = 1 volt, ha T = 12600 K; tehát szobahômérsékletû, vagyis kereken 300 K hôfokú katódból az elektronok alig 0,03 volt sebességgel lépnek ki és csupán az ettôl eredô, elenyészôen csekély visszahatást közlik vele: Azontúl pedig a kapcsolat a katód és a kilépett elektronok között megszûnik; az elektronok további gyorsításukat nem a katódtól eredô taszítástól, hanem az anódtól származó vonzástól (óvatosabban kifejezve: a villamos térerôtôl) nyerik és a katódra visszaható erô is ettôl ered. Ennek részletes taglalását most mellôzve, megemlítjük, hogy Riecke 1898-ban a sugarak tehetetlen tömegét ugyancsak a katódra gyakorolt visszahatás mérésével próbálta kimutatni. Ilyen visszahatást tapasztalt is, ez azonban 30-szor nagyobb volt annál, mint amekkorát az áram- és feszültségmérés alapján várni lehetett és nyilvánvalóan a radiométer-erôktôl származott. Ezeknek zavaró hatását Angerernek sem sikerült kiküszöbölni 1913 ban végrehajtott gondos vizsgálataiban. Ô volt egyébként az elsô és egyetIen vizsgáló, aki izzókatóddaI dolgozott. A felgyorsított elektronokat eredeti irányukból 90o-kal eltérítve, nyílással ellátott üreges alumíniumgömböcskébe fogta fel, amely torziós mérleg karjára volt függesztve s az erre gyakorolt nyomást a szokott módon, a karnak tükörleolvasással megfigyelt elfordulásából határozta meg. Az így nyert adatok azonban a számítás szerint várható értékeket nála is sokszorosan (3 . . . 16-szor) felülmúlták
Most, utólag, könnyû belátni, hogy mindezen vizsgálatoknak szükségszerûen kudarccal kellett végzôdniök, egyrészt mivel a radiométer-erôket csupán a mai segédeszközökkel elôállítható, legjobb vákuumban lehet elég kicsiny értékre leszorítani, másrészt, mivel mind e kutatók igen nagy feszültségû, de igen kis intenzitású sugarakkal dolgoztak. Hideg katóddal persze nem is lehet mást elôállítani, azonban a felfogott sugarak erôssége Angerernél sem haladta meg a mikroampért, a gyorsító feszültséget ellenben 2500 és 14000 volt között változtatta. Hogy ez miért nem helyes és hogyan kell helyesen eljárnunk, erre könnyû rájönni, ha a kísérleteknél várható viszonyokat kissé jobban szomügyre vesszük.
Mindenek elôtt számítsuk ki a katódsugarak nyomását. Ezt elemi meggondolásokkal elvégezhetjük.
Ha másodpercenként N számú, v sebességû, m tömegû lövedék ér egy felfogó felületet amelyben azok fennakadnak, vagyis sebességüket teIjesen elvesztik , akkor a felületre gyakorolt nyomás (P) a mechanika jól ismert törvényei értelmében egyenlô a másodpercenként felfogott és megsemmisült mozgásmennyiséggel, vagyis
(1) P = N · m · v
Ha U az elektronokat gyorsító feszültség, akkor az energia-megmaradás törvénye értelmében felírhatjuk, hogy
(2) e · U = 1/2 mv2 és ebbôl
(3) v = (2e/m)1/2· U1/2
Legyen az elektronáram erôssége, azaz a mp-enként átvitt töltés mennyisége I, akkor nyilván a mp-enként átrepülô elektronok száma
(4) N = I/e és N és v értékeit az (1) egyenletbe helyettesítve kapjuk, hogy
(5) P = (2 m/e)1/2 · I · U1/2 avagy ide e/m értéket betéve és I-t milliampérben, U-t voltban mérve
(6) P = 3,37 · I · U1/2 · 104 dyn
Az (5) ill. (6) egyenletbôl érdekes következtetéseket lehet levonni. Láthatjuk ami egyébként magától értetôdô , hogy a nyomás az. elektronsugarak áramerôsségével egyenesen arányos, ellenben a feszültségnek csupán 1/2-ik hatványa szerint nô, tehát a mérendô nyomást könnyebb az áramerôsség. növelésével fokozni, mint a feszültséggel. De még egy másik, döntô szempont is e mellett szól. A felfogó testen az elektronsugár egész energiája W = I · U hôvé alakul. Ez pedig U-val is egyenesen arányos. Ha tehát a feszültséget mondjuk megszázszorozzuk, péIdául 100 voltról 10000 voltra emeljük, a sugarak nyomása csak tízszer lesz nagyobb, de a hôfejlôdés, tehát a zavaró radiométer-erôk is, a százszorosára nônek! E szerint tehát az ütközô elektronok nyomásának kimutatására nem sokezer volt feszültségû, de alig mikroampér erôsségû "katódsugarak", hanem kicsiny feszültségû, de nagy áramerôsségû "elektronáramok" alkalmasak, olyasfélék, mint aminôk egy rádiócsôben folynak. Legyen például U = 100 volt és I = 10 mA, ami nagyon könnyen megvalósítható, akkor a (6) egyenlet szerint a nyomás 0,034 dyn, azaz kereken 1/30 milligramsúly, ez peeig a fizikus szemével nézve éppenséggel nem kicsiny erô.
 |
| 1.kép |
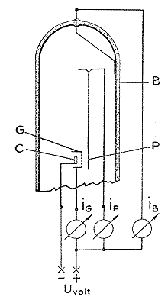
Az 1. kép mutatja vázlatos oldalnézetben e sorok írója által még 1939-ben eredményesén használt kísérleti berendezést, amely a fenti megfontolások alapján készült s valóban nem más, mint egy kissé módosított háromelektródás elektroncsô. A képen C a csônek a papiros síkjára merôleges, közvetett vagy közvetlen fûtésû katódja; ezt három oldalról körülveszi a fémlemezbôl készült G rács (gyorsító-elektród), amelyen a katóddal szemben hosszúkás, dróthálóval fedett nyílás van, és P az ingaszerûen felfüggesztett anód vagy felfogó-elektród. Az egész szerkezetet a képen fel nem tüntetett szokásos üvegláb hordja és csôalakú, kb. 35 mm átmérôjû búrába van beforrasztva. A búra belsô falát elôzetesen, esetleges fal-töltések levezetése céljából, katódporlasztás segélyével a B vékony aranybevonattal láttuk el a megfigyelésre két szemközti ablakot szabadon hagyva , majd a beforrasztás után a csôgyártásban szokott módon gondosan kiszivattyúztuk és leforrasztottuk.
 |
|
2.kép |
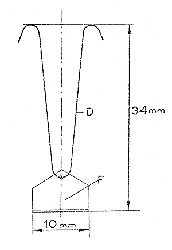
A 2. kép mutatja az anód szerkezetét és méreteit. Ez úgy készült, hogy egy közönséges, az elsô bekapcsoláson már át is esett 110 voltos, 15 wattos feszítettszálú izzólámpát feltörve, izzószálából egy U alakú darabot kivágtam és az alsó hajlatára egyetlen csepp vezetô-ragasztóval (néhány csepp karamell-oldattal vegyített kolloid-grafittal) az aranyfüstbôl kivágott F felfogó lemezkét odaragasztottam. Az aranyfüst lemezke alsó szélét merevítés végett felhajlítottam s a katód felé forduló oldalát a másodlagos elektronkibocsátás megakadályozása végett bekormoztam. Az egész "inga" súlya kereken 1 mg volt; ezt mikromérlegen 1/100 mg pontossággal lehetett meghatározni. Hogy az inga kilengésébôl a reá ható erôt kiszámíthassuk, a súlyán kívül a súlypont helyzetét is ismerni kell; ezt a beszerelés elôtt egy keresztbe fektetett varrótûn való kiegyensúlyozással határoztam meg.
A kísérletekben használt egyszerû kapcsolást az 1. képen ugyancsak láthatjuk. A katód fûtôkörét nem rajzoltuk fel; az U feszültség (gyorsító feszültség) negatív sarka természetesen a katódhoz volt kapcsolva, míg a rács, az inga és a falbevonat egy-egy milliampérmérô közbeiktatásával közösítve a pozitív sarokkal volt összekötve. A három mûszer közül mérésre csupán a középsô szolgált, amely az ingán át Iefolyó elektronáramot mérte; a másík kettôt inkább csak ellenôrzés végett iktattam az áramkörbe. A tulajdonképeni mérés elôtt meggyôzôdtem arról, hogy a rács a katódot az inga-anóddal szemben elektromosan olyan tökéletesen árnyékolta, hogy az U feszültséget 250300 voltra is növelhettem a nélkül, hogy az ingán a katódtól eredô elektrosztatikus vonzásnak, vagyis az ábra szerint balfelé való kilengésnek a legkisebb nyoma is észlelhetô lett volna. Ha azonban a katód fel volt fûtve és a csôre feszültséget adtunk, az inga jobbra kitért, kihajlott, bizonyítván, hogy itt valóban a várakozásunk szerinti jelenség játszódik le: a katódból kilépô elektronok az U feszültség által felgyorsítva, a rács nyílásain kirepülnek és az ingába ütközve, arra nyomást fejtenek ki. A jelenség a maga egyszerûségében elôadási kísérletnek is alkalmas. Az inga árnyképét kivetítjük s az U feszültséget célszerûen potenciometerrôl vesszük le; ekkor szépen be lehet mutatni, hogy mint nô és csökken az inga kitérése a szerint, amint a feszültséget növeljük vagy csökkentjük, sôt amirôl még alább szó lesz a kitérésbôl e/m viszony közelítô értékét is kiszámíthatjuk. (E kísérletet más, vele rokon jelenségekkel együtt elsôízben a Magyar Elektrotechnikai Egyesület 1939 május 9-i ülésén mutattam be.) Tájékozásul szolgálhat az az adat, hogy a fentebb említett 100 V, 10 mA erôsségû áram az inga alsó végét jó egy milliméterrel téríti ki; ennél nagyobb kitérést csak azért nem lehetett létrehozni, mivel az aranyfüst Iemezke az elektronok bombázásától már jóval kisebb, kb. 1/3 watt terhelésnél izzásba, és pedig nem vörös, hanem az aranyra jellemzô sajátságos fakózöld fényû izzásba jött.
A fenti szerkezetû csövekkel több sorozat mérést is végeztem az elektronsugarak nyomásának és ebbôl az e/m viszonynak meghatározására. A villamos kapcsolás a legegyszerûbb esetben azanos volt az 1. képen láthatóval. Mérendôk voltak: az U gyorsító faszültség, az inga által .levezetett Ip elektronáram és az inga kitérése. Ez utóbbi mérésére kb. 22-szeres nagyítású, okulár-mikrométerrel ellátott, vízszintes tengelyû leolvasó mikroszkóp szolgált; az "érzékenység", vagyis az egy osztásrésznyi kitérést okozó erô, az ingák súlyából és méreteibôl számítva, 12 ... 14 · 104 dyn volt, úgy, hogy pl. 35 voltos, 1 mA erôsségû elektronsugár már két osztásrész kitérést okozott és a tizedeket tûrhetôen lehetett becsülni. Az alábbi táblázatban példaképen közöljük egy mérési sorozat eredményét:
| U (V) | Ip (mA) | a | Pm | Psz | Pm/Psz | 108·e/m (coul/g) |
| 30 | 1,0 | 1,6 | 21,3 | 18,5 | 1,15 | 1,32 |
| 40 | 1,5 | 2,8 | 37,3 | 32,0 | 1,17 | 1,30 |
| 50 | 2,05 | 4,3 | 57,2 | 49,0 | 1,17 | 1,28 |
| 60 | 2,61 | 6,0 | 80,0 | 68,0 | 1,18 | 1,28 |
| 70 | 3,16 | 7,0 | 105 | 89,0 | 1,18 | 1,27 |
| 90 | 4,0 | 12,5 | 166 | 144 | 1,15 | 1,32 |
| 100 | 4,9 | 14,0 | 186 | 165 | 1,13 | 1,39 |
A táblázat elsô két oszlopa nem szorul magyarázatra. A harmadik oszlopba írt számok: az inga kitérése, osztásrészekben; Pm a mért nyomás 104 dynben (vagyis az "érzékenység" és az a kitérés szorzata); Psz az U-ból és Ip-bôl a (6) képlet szerint számított nyomás; Pm/Psz a kettô hányadosa s végül e/m a töltés és tömeg viszonya, amint az a mért nyomásból, az (5) egyenlet megfordításaként adódó
(7) e/m = 2 · 108 · I2 · U/P2 képlet szerint kiszámítható. (Itt I milliampérben, U voltban, P pedig 104 dynben értendô.)
A hatodik oszlop megtekintésébôl kiderül, hogy a mért nyomás a számítottnál rendszeresen nagyobb volt, éspedig kereken 15%-kal. Ennek következtében az e/m viszonyra átlagban 30%-kal kisebb értéket kaptam, mint az általánosan elfogadott érték, s mivel ez utóbiban kételkedni semmi okunk nincsen, nyilván a mérésekben voltak rendszeres hibák. Két ilyenre reá is mutathatunk. A fentiekben, egyszerûség kedvéért, elhanyagoltuk a rács és inga között fellépô negatív tértöltések hatását, amit vagy mint az elektronokat lassító potenciál-minimumot, vagy ami ugyanarra vezet mint az ingát visszatartani igyekvô elektrosztatikus vonzást kell tekintetbe venni. Ha ezt megtesszük, a mért és számított értékek különbsége még 25%-kal nagyobb lesz. Ellenkezô értelemben változtatja meg a mérési eredményt az a körülmény, hogy az elektronok által bombázdtt inga maga is elektronokat bocsát, vagy bocsáthat ki. Ez az ú. n. másodlagos emisszió az I-t hamisítja meg, mivel a leolvasott érték, az ingán át lefolyó áram amibôl a számított nyomás ádódik , természetesen csupán a különbsége a reá lövelt és az általa kibocsátott elektronáramnak, holott a nyomást amit az inga kítérésével mérünk az egész primér áram hozza létre. Az ebbôl származó hiba minden mértéket meghaladhat. Ha például az inga nincsen bekormozva és oxid-katóddal dolgozunk, akkor az errôl elpárolgó és az ingára lerakódó bárium ennek kibocsátó képességét annyira megnöveli, hogy pl. 250 volt gyorsító feszültség esetén háromszor akkora nyomást mérünk, mint amennyi az Ip értékébôl számítással adódik, vagyis az inga 2/3 annyi elektront, mint amennyit rálöveltünk, újra kibocsát s csak az 1/3 rész folyik az ingán le. Ez áll az 1. kép szeriniti kapcsolás esetén, midôn a rács és az inga ugyanazon a feszültségen van. Ha pedig az inga és rács közé még egy kisebb u feszültséget is kapcsolunk, pozitív sarkával a rácsra, és ezzel a másodlagos kibocsátást elôsegítjük, akkor meglepô eredményekhez jutunk. Már u = 10 voltnál az eredetileg 1,2 mA erôsségû inga-áram zérus lesz: az inga ugyanannyi elektront bocsát ki, mint amennyit rálöveltünk, de a nyomás, az inga kitérése, változatlanul 12 osztásrész marad és nem változik meg u = 15 volt esetén sem; amikor pedig az inga-áram már elôjelét változtatja és értéke 0,35 mA, vagyis ennyivel több elektron hagyja el az ingát, mint amennyi érte. Megemlíthetem azt is, hogy csöveinkben a radiométer-hatás sem volt teljesen kiküszöbölve, azonban ennek részletezésébe annál kevésbbé óhajtok kitérni, mivel kezdettôl fogva sem volt szándékomban pontos méréseket végezni.
Egy elvi szempontra azonban még rá kívánok mutatni.
Ma nem akad fizikus, aki kételkedne abban, hogy az elektronnak anyagi tömege is van, halott erre közvetlen bizonyítékunk mindeddig nem volt. Az elektromos és mágneses eltérítés ismeretes törvényei ugyanis ezt nem bizonyítják; pontosan megfogalmazva csupán azt állíthatjuk, hogy a két jelenség helyes leírásához jutunk, ha feltesszük, hogy az elektronnak e töltése és m tömege van és reájuk alkalmazzuk a mechanika és elektromosságtan törvényeit. De e feltevés nem szükségszerû. Hertz Heinrich például, mikor a katódsugarak mágneses hatását hasztalanul próbálta kimutatni, megkockáztatta azt a feltevést, hogy a katódsugár talán valami hullámszerû, talán az éter longitudinális rezgése és a mágneses eltérítés olyasvalami, mint a fény polárossági síkjának elfordulása mágneses térben. Egy példa jobban meg fogja világítani, hogy mire célzunk. A Zeeman-jelenség és annak közismert Lorentz-féle elmélete annak idején szintén olyan "kézzelfoghatóan" látszott bizonyítani a fénykibocsátás (klasszikus) magyarázatát: hogy az n frekvenciájú fény n frekvenciával rezgô elektronoktól ered és a mágneses tér ezt a maga elektrodinamikus erôivel befolyásolja, hogy ebben sem kételkedett senki. De nem telt bele alig két évtized, és maga Lorentz állapította meg és ez bizonyítja ennek a tudósnak emberi nagyságát hogy "ennek a magyarázatnak már csupán történelmi értéke van". A Zeeman-jelenségre vonatkozó kísérleti adataink azonban a magyarázattól függetlenül megmaradnak. Ugyanezt a meggondolást a mi esetünkre alkalmazva azt kell mondanunk: ámbár nagyon kevéssé valószínû, hogy a katódsugarak villamos és mágneses eltérítését valaha is másképen fogjuk értelmezni, mint ahogyan ötven évvel ezelôtt Thomson J. J. értelmezte, de ha ez be is következnék, az a kísérleti tény, hogy egy U feszültségre felgyorsított I erôsségû elektronáram az útjába helyezett akadályra a (6) egyenlet által megadott értékû mechanikai nyomást fejt ki, változatlanul fennáll. Ez pedig addig, amíg a mechanika a mai értelemben érvényben marad, másképen valóban nem értelmezhetô, minthogy a szóban forgó áram a másodpercenkénti I töltéssel együtt a (6) szerinti mozgásmennyiséget is átszállítja.
| Természettudomány, | III. évfolyam. 1948. 311317. oldal https://www.kfki.hu/chemonet/TermVil/ https://www.ch.bme.hu/chemonet/TermVil/ |