Holográfia az atomi skálán
Az emberi gondolkodást már az õsidõk óta foglalkoztatja a szabad szemmel nem látható világ, a mikrovilág. Ez a kíváncsiság vezetett a XVI. században a fénymikroszkóp, az 1940-es években az elektronmikroszkóp és napjainkban a pásztázó alagút, ill. atomerõ mikroszkópok felfedezéséhez. Ez utóbbiak már az atomi távolságokat is képesek felbontani. A fenti módszerek a vizsgált tárgy direkt nagyított képét adják, és elsõsorban a felületrõl kaphatunk információt. Az anyagok belsejébe való betekintést a kb. 100 éve felfedezett röntgensugárzás tette lehetõvé. Számos, a röntgensugárzáson alapuló diffrakciós módszer fejlõdött ki az atomi szerkezet vizsgálatára. Ezek azonban nem közvetlen képet szolgáltatnak, hanem olyan adatsort, amin még egy matematikai Fourier-transzformációt kell végrehajtani, hogy az atomok valós térbeli elhelyezkedését megkapjuk. Elvben egy ilyen transzformáció megkívánja a mért hullámok (esetünkben a röntgenfotonok) intenzitásának és fázisának ismeretét.
Egy diffrakciós méréskor azonban csak a fotonok számát (tehát a hullám intenzitását) kapjuk meg, a fázisát nem. A hiányzó fázisinformációt különbözõ módon pótolhatjuk. A leggyakoribb valamilyen független mérés adta szerkezeti információ, de sokat segíthet, ha már van valamilyen elõzetes elképzelésünk a várt atomi rendrõl. Ezek beépítése a diffrakciós adatok kiértékelésébe a gyakorlatban lehetõvé teszi a kristályban található pontos atomi rend meghatározását.
Sok esetben azonban nem lehetünk egészen biztosak a megoldott szerkezetben. Ezen túl elvileg is nagy jelentõségû lenne olyan módszer kidolgozása, ami mentes az elõzõekben említett bizonytalanságtól. Továbbra is fennáll tehát a kérdés: van-e a kezünkben olyan mérési lehetõség, ami a vizsgálni kívánt objektumok 3D térbeli rendjérõl teljes információt (tehát intenzitást és fázist) ad. Körültekintve a különbözõ vizsgálati technikák között, azt találjuk, hogy a szemmel látható tárgyak világában már kb. 50 éve megoldották, hogyan lehet rögzíteni egy 2D fotolemezen a tárgy 3D képét úgy, hogy azt késõbb könnyûszerrel ismét 3D-ban lássuk. A módszer neve holográfia, és felfedezése Gábor Dénes nevéhez fûzõdik [1].
 |
 |
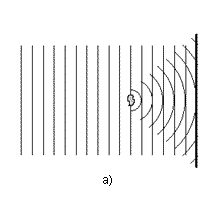
| 1. ábra. Hologramok felvételére leggyakrabban használt két elrendezés. Az (a) esetben a referencianyaláb síkhullám. Ennek egy része akadálytalanul éri el a detektáló felületet, míg egy másik része szóródik a tárgyon, és ez a szórt hullám (tárgyhullám) meg a referencianyaláb együttesen alakítja ki a detektoron mérhetô intenzitáseloszlást, ami a hologram. A (b) ábrán egy pontszerû forrásból indul a referencianyaláb, amely most gömbhullám. A hologram kialakulása hasonló az elôzô esethez, de maga a hologram teljesen más lesz, mivel a referenciahullám is más. | |
Hogyan is mûködik a holográfia? A vizsgált tárgyat egy monokromatikus és koherens fényforrással világítjuk meg. A fény egy része szóródik az objektumon (tárgyhullám T), a másik része pedig akadálytalanul halad tova (referenciahullám R) a detektáló felület felé (1. ábra). A tárgy és a referenciahullámok összegét érzékeli a detektor. Miért jó ez? Detektoraink (pl. a film) csak az intenzitást képesek rögzíteni, tehát valahogyan intenzitásváltozássá kell alakítanunk a fázisinformációt. Ebben segít a referenciahullám. Mivel ennek fázisa valamilyen jól meghatározott (általunk ismert) módon változik, ha ehhez viszonyítjuk a szórt hullámok fázisát és ezt a különbséget képesek vagyunk mérni, ez elég a tárgy 3D képének elõállításához. Részletes elemzés azt mutatja, hogy a fotolemezen a fenti módon rögzített intenzitáseloszlást elégséges a referencianyaláb inverzével megvilágítani, és visszakapjuk a tárgy 3D képét. A felfedezés óta eltelt ötven évben a holográfia nagy utat járt be, és napjainkban széles körben alkalmazzák a tudományban, ipari technológiákban és a mindennapi életben is. Felmerül a kérdés, miért ne használhatnánk akkor az atomi rend felderítésére. Sajnos ez „csak úgy egyszerûen” nem lehetséges. Ennek oka, hogy a holográfia térbeli felbontását nem növelhetjük a végtelenségig. A felbontás határát több tényezõ együttesen adja: 1. az alkalmazott hullámhossz, 2. a detektáló felület felbontása, vagy a hullámforrás mérete. Ezekbõl világosan kiderül, hogy a hagyományos fénnyel készült hologramok nem adhatnak információt az atomi távolságokról (hiszen mind a forrásméret, mind a hullámhossz a mikronos tartományba esik). Milyen technikai lehetõségek vannak a hullámhossz és a forrás-, ill. detektorméret csökkentésére? Rövidebb hullámhosszú jó koherenciatulajdonságokkal rendelkezõ elektromágneses sugárzást kaphatunk szinkrotron sugárforrásokban elhelyezett ún. undulátorokból. Ezzel a holográfiára használható sugárzás hullámhossza egészen a 100 Å tartományig csökkenthetõ. A forrás-, ill. detektorméret kb. 300 Å-re redukálható csúcstechnológiákat felhasználva. Ezek az értékek még mindig sokkal nagyobbak, mint a kb. 1 Å-ös atomi méretek. Hogyan tovább? Az áthidalandó két nagyságrend egy teljesen új szemléletmódot, új ötletet kívánt. A megoldás alapötlete LarryBarteltõl és Szõke Ábrahámtól (Kaliforniában élõ magyar származású kutatótól) származik [2, 3]. Azt javasolták, hogy magukat a mintában található egyedi atomokat használjuk, mint forrásokat. Ismeretes, hogy az atomi elektronok gerjesztése után több olyan folyamat is végbemehet, amelynek eredménye rövid hullámhosszú sugárzás kibocsátása. A sugárzás megjelenhet elektronhullám (pl. Auger- vagy fotoelektronok) vagy elektromágneses hullám (fluoreszcens sugárzás) formájában. Ezeket a folyamatokat felhasználva egyszerre megoldódik a hullámhossz- és a forrásméret-probléma. Tehát ebben az esetben a kiválasztott atom mint egy lámpás megvilágítja környezetét, és errõl kaphatunk hologramot.
Részletes elméleti megfontolások után kiderül, hogy az elektronok használata kedvezõbb a megfigyelhetõség szempontjából. Ennek oka, hogy az elektronok atomokkal való kölcsönhatása nagyságrendekkel erõsebb, mint a fotonoké, így a hologramban megjelenõ intenzitásoszcillációk is sokkal nagyobbak. Nem csoda tehát, hogy elõször elektronokat használtak atomok holografikus leképzésére [2,4].
Ezen a ponton a figyelmes olvasó megkérdezheti, hogyan tudunk a makroszkopikus minta sok atomjából pontosan egyet kiválasztani, és arra késztetni, hogy csak õ maga sugározzon és a többi atom ne. Nos a kérdés jó, és a válasz az, hogy gyakorlatilag nem lehetséges egy atom kiválasztása, mint forrásé. Mit tehetünk ekkor? A megoldást egy speciális minta választása adja. Olyan mintát kell készíteni, amelyben minden forrásatom ugyanazt a hologramot és ugyanoda hozza létre. Ezek a feltételek egy egykristályminta esetén teljesülnek, hiszen egy meghatározott krisztallográfiai pozícióban elhelyezkedõ atomok környezete azonos, és ha a minta méretéhez viszonyítva távol helyezzük el a detektáló felületet, akkor az egyes atomok által létrehozott hologramok ugyanarra a helyre esnek. Az elektronokkal végzett kísérletek egyértelmûen bizonyították a belsõforrás-elv helyességét. Azonban mint minden, az elektronok számlálásán alapuló technika, ez is csak nagyvákuumban végezhetõ, és csak a felületközeli rétegekrõl ad információt, az elektronok kis szabad úthossza miatt. Ezért igen hasznos lenne, ha elektromágneses hullámokkal, azaz röntgensugárzással is végre lehetne hajtani a kísérletet.
Bár az elektronokkal felvett elsõ hologram 1990-ben készült,
és azóta is sok ilyen kísérletet végeztek,
az elvben ugyanúgy mûködõ röntgenholográfia
sokáig nem fejlõdött ki. Ennek oka a fotonoknak az atomokkal
való viszonylag gyenge kölcsönhatása. Ez két
zavaró effektusban nyilvánul meg: egyrészt a holografikus
oszcilláció igen kis amplitúdójú (kicsi
a jel/zaj viszony), másrészt a hosszú távú
transzlációs szimmetria (kristályos rend) és
a fotonok nagy szabad úthossza miatt erõs diffrakciós
csúcsok (Bragg-reflexiók) jelennek meg. Ezek a tényezõk
évekig megakadályozták röntgen-hologramok felvételét.
 |
 |
| 2. ábra. A mérés vázlata
(a mûködés leírását lásd
a szövegben)
és a megvalósított berendezés a szerzôkkel |
A megoldás végül is két részletben született meg: elõször megmutattuk, hogyan lehet elválasztani a forráshoz közeli és távoli atomok járulékát, kiszûrve ezzel a Bragg-csúcsokat [5], késõbb olyan mérési elrendezést hoztunk létre, amely optimális az effektus kimutatására [6]. (Az elrendezést a 2. ábra mutatja.) A mûködés röviden a következõ. A röntgenforrásból kilépõ több energiát tartalmazó sugárzás egy monokromátorra esik, amely kiválasztja a mintában lévõ atomok gerjesztéséhez szükséges energiájú fotonokat. Ez azt jelenti, hogy nagyobb fotonenergiát kell választanunk, mint a kilökni kívánt elektron kötési energiája. A nyaláb ezután a mintára esik egy tetszõleges, de a mérés során rögzített szögben. Így a mérés ideje alatt a mintában folytonosan keletkeznek gerjesztett atomok, melyek csak nagyon rövid ideig léteznek ebben a magas energiájú állapotban, mivel a kilökött elektronok helyére a külsõ héjakról elektronok „esnek be”. Az eközben kibocsátott fotonok energiája megegyezik a két atomi nívó közötti energiakülönbséggel. Ezeket az úgynevezett fluoreszcens fotonokat használjuk a hologram létrehozására. A kibocsátott fotonok két úton juthatnak el a detektorba:
(1) a minta valamely atomján való szóródás
után (tárgynyaláb);
(2) a többi atommal való kölcsönhatás
nélkül (referencianyaláb).
A detektorral letapogatva a különbözõ irányokban mérhetõ fluoreszcens intenzitást, vagyis a két hullám interferenciájának eredményét: a forrásatomot környezõ atomok hologramját mérhetjük.
Ugyan ezzel a kísérlettel bebizonyítottuk a módszer mûködõképességét, azonban ez még nem vezet közvetlenül a gyakorlati életben való széles körû alkalmazáshoz. Ehhez még számos további problémát kell kiküszöbölni. Az elmúlt négy évben ezek megoldásán dolgoztunk, és napjainkra jutottunk el oda, hogy e technikával olyan kérdéseket válaszolhatunk meg, amik más módszerekkel nehezen elérhetõk. A következõkben körvonalazzuk a fejlesztés legfontosabb lépéseit, s végül egy példát mutatunk az alkalmazásra.
Kísérleteink másokat is arra ösztönöztek, hogy röntgenholografikus méréseket végezzenek. Ezek között jelentõs eredmény is született: egy amerikai–német nemzetközi kutatócsoport olyan kísérletet végzett, amelyben az atomokat nem sugárforrásként, hanem piciny pontszerû detektorként használták [7]. Ekkor a hologramot a külsõ forrásból érkezõ röntgennyaláb hozza létre. A beesõ sugárzás a kiválasztott detektoratomunkat elérheti direkt módon (referencianyaláb), tehát minden elõzetes kölcsönhatás nélkül, vagy szóródhat is a környezõ atomokon (tárgyhullám), és ezután kerül kölcsönhatásba a detektoratommal. Tehát végeredményben a fenti két folyamatból adódó hullámok összege együttesen gerjeszti a detektoratomot, ami a gerjesztéssel arányos fluoreszcens sugárzást bocsát ki. Ha a mintához képest változtatjuk a beesõ nyaláb irányát, a két nyaláb összege is változik, és a fluoreszcencia erõssége ezt tükrözi.
A beesõ nyaláb irányának függvényében felvéve a fluoreszcens intenzitást, hasonló hologramot kapunk, mint belsõ forrással. Ezt a módszert inverz holográfiának is hívjuk mivel felcseréltük a detektor és a forrás helyét. Az inverz mód elõnye, hogy nagyobb összintenzitást ad és a hologramformáló nyaláb hullámhossza szélesebb tartományban szabadon választható.
A továbbiakban a normál és az inverz módot
nem választjuk szét, mivel mindkettõnél hasonló
problémák merülnek fel, és fejlesztésüket
is párhuzamosan végeztük. E kis kitérõ
után visszakanyarodunk eredeti gondolatmenetünkhöz. Tehát
arról fogunk beszélni, milyen fejlesztéseket végeztünk
az elmúlt négy évben.
 |
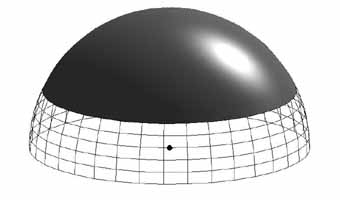 |
| 3. ábra. Az Európai Szinkrotron Sugárforrás, ami közel egy kilométer kerületû (Grenoble) | 4. ábra. A teljes hologramnak csak azt a tartományát tudjuk megmérni, amelyet a félgömbön sötét színnel ábrázoltunk. A minta síkja a félgömb alsó síkjával esik egybe, és a minta a gömb középpontjában van. |
Elõször a mérési idõt csökkentettük.
Az elsõ mérés kb. 2 hónapot vett igénybe.
Jelenleg néhány perc alatt tudunk egy hologramot felvenni.
Ezt a sugárforrás hagyományos röntgengenerátorról
szinkrotron forrásra (3. ábra) való cseréjével
és a mérõberendezés nagy intenzitásra
való átépítésével értük
el. Másodikként kifejlesztettünk egy olyan kiértékelést,
amely az eredetileg erõsen anizotrop valós térbeli
felbontást megjavította és közel izotroppá
tette. Az anizotrópiát az okozza, hogy technikai okok miatt
nem tudjuk a teljes hologramot megmérni (vagyis a minta körüli
teljes gömbfelületen feltérképezni a fluoreszcens
intenzitást), hanem csak egy sokkal kisebb gömbsüvegen
(4.
ábra). A hiányzó rész miatt a 3D-rekonstrukcióban
a minta felületére merõleges irányban az atomok
képe elnyúlt lesz. Ezt úgy korrigáltuk, hogy
a minta kristályos voltát felhasználva a mért
hologramot kiegészítettük a teljes térszögre
(5.
ábra) [8]. Legutóbb pedig azon dolgoztunk, hogy a nehéz
atomok mellett a könnyûeket is le tudjuk képezni. Sikerült
egy NiO-mintában a Ni-atomokon kívül az oxigénatomok
képét is megkapnunk [9]. Ezt úgy értük
el, hogy sokkal jobb statisztikával mértünk (vagyis
a kép egy-egy pontjában sokkal több fotont gyûjtöttünk),
és csökkentettük a szisztematikus hibákat is pl.
a szórt sugárzás elleni jobb árnyékolással,
a beesõ nyaláb pontosabb monitorozásával, stabilabb
mechanika alkalmazásával stb. Ez az eredmény megnyitja
az utat szerves vegyületek vizsgálata felé.
 |
 |
| 5. ábra. Balra egy CoO-mintában a Co-atomok teljes gömbre való kiterjesztett hologramját, jobbra pedig az ebbôl rekonstruált 3D képet láthatjuk, amely a Co-atomokat ábrázolja | |
Az elõbbiekben leírt fejlesztések után mérõrendszerünk már elég megbízhatónak tûnt ahhoz, hogy olyan probléma megoldását tûzzük ki célul, ami más módszerekkel nem, vagy csak nehezen oldható meg. Megkíséreltük egy kvázikristály holografikus leképezését. A kvázikristályok olyan anyagok, amikben nincs hosszú távú periodikus rend, ugyanakkor mégsem teljesen rendezetlenek. Néhány jól meghatározott alakzatból teljes térkitöltéssel építhetõk fel. Ez maga után vonja, hogy van bennük orientációs rend. A röntgendiffrakciós képük éles csúcsokból áll, de mégsem indexelhetõk be az ismert 3D-tércsoportoknak megfelelõen, hanem csak valamilyen magasabb dimenziós periodikus rács segítségével. Így viszont a pontos 3D atomi elrendezõdés (amit ilyen anyagoknál atomi dekorációnak szoktak nevezni) sem kapható meg hagyományos diffrakciós mérésekbõl. Mivel az általunk alkalmazott röntgenholográfia egy kiválasztott atom körüli 3D-rendet adja meg, segítségével legalább az adott típusú atom körüli néhány környezet átlaga látható direkt módon. Egy AlPdMn kvázikristályban a Mn körüli atomok hologramját láthatjuk a 6. ábrán. Jellegzetes az ötfogású szimmetria, amely hagyományos kristályos anyagoknál nem jelenhet meg. Az ennek nyomán kapott 3D valós térbeli képet is bemutatja a 6. ábra [10]. Végül e szakasz befejezéseként meg kell említenünk egy tényezõt, amely jelenleg még igencsak leszûkíti a lehetséges alkalmazások területét: megbízható, jó minõségû hologram viszonylag nagy, síkfelületû mintáról készíthetõ. Ez nem elvi, hanem gyakorlati probléma, de jelenleg nem látunk egyszerû utat a megoldására.
 |
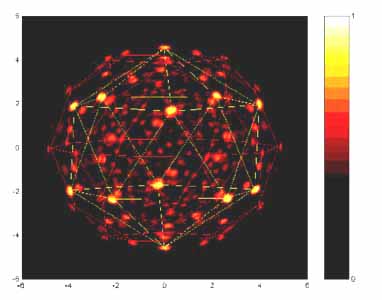 |
6. ábra. Egy AIMnPd-kristályban a Mn-atom körül elhelyezkedô szomszédok hologramjából (balra) rekonstruált valós térbeli kép (jobbra). A legerôsebb pontok egy ikozaéder csúcsain helyezkednek el. Ezek felelnek meg a különbözô típusú atomok alkotta átlagos környezetnek. Az eredmény egyezik az elmélet alapján modellszámításokból várt atomi elrendezéssel.
Annak ellenére, hogy még jócskán van teendõ a holográfia fejlesztésével kapcsolatban, érdemes néhány szót szólni a lehetséges alkalmazási területekrõl. A gyakorlat azt mutatja, hogy egy módszer alkalmazási területei akkor jelentkeznek igazán, amikor már viszonylag széles körben kezdik használni. Atomi felbontású holografikus méréseket ugyan a világon csak néhány laboratóriumban végeznek, ettõl függetlenül a módszer néhány felhasználását már most is megjósolhatjuk. Ilyenek:
1. hagyományos diffrakciós mérések kiértékelésénél
segítséget nyújthat a fázisok rögzítésére,
így meggyorsítva és biztosabbá téve
a szerkezetmegoldást;
2. alacsony koncentrációban jelenlévõ szennyezõ
atomok környezetének vizsgálata;
3. félvezetõkben található adalékatomok
körüli atomi rend meghatározása;
4. biológiai molekulák aktív helyein ülõ
fématomok környezetének feltérképezése
stb.
Ezek a problémák már megoldhatók a jelenleg rendelkezésre álló technikai eszközökkel. Ha egy kicsit távolabbi jövõbe tekintünk, további érdekes alkalmazásokat láthatunk. Nagyon erõs röntgenforrások és gyors detektorok használata, kombinálva gyors számítógépes adatfeldolgozással lehetõvé teheti, hogy egy hologramot ms idõskálán vegyünk fel, így valós idõben követhetjük a lassú atomi mozgásokat. Egy további lehetõség, hogy az atomi fluoreszcencia helyett az atommagokból kibocsátott gammasugárzást használjuk, mint „megvilágító” nyalábot. Ez olyan elõnyökkel jár, mint kisebb forrásméret, és ezáltal jobb térbeli felbontás, érzékenység az anyag belsejében kialakult mágneses és elektromos terekre. Ilyen típusú mérések közül az elsõt már el is végezték [11], de a valódi alkalmazások még hátra vannak.
Reméljük, hogy e rövid áttekintéssel
érzékeltettük, hogy a röntgenholográfia
belépett az atomi szerkezetet vizsgáló módszerek
közé. Azonban az is világos, hogy szélesebb körû
felhasználásához még további technikai
és elméleti problémákat kell megoldanunk.
Irodalom
D. Gabor, Nature (London) 161, 777–778 (1948).
L. S. Bartell and C. L. Ritz Science 185, 1163 (1974).
A. Szöke, in Short Wavelength Coherent Radiation: Generation and
Applications, ed. by D. T. Attwood and J. Boker, AIP Conference Proceedings
No. 147 (American Institute of Physics, New York, N. Y.) 361–367 (1986).
G. R. Harp, D. K. Saldin and B. P. Tonner, Phys. Rev. Lett. 65, 1012–1015
(1990).
5. M. Tegze and G. Faigel, Europhys. Lett. 16, 41–46 (1991).
6. M. Tegze and G. Faigel, Nature 380, 49 (1996)
7. Gog T, Len P M, Materlik G, Bahr D, Fadley C S, and Sanchez-Hanke
C Phys. Rev. Lett. 76, 3132 (1996).
8. M. Tegze, G. Faigel, S. Marchesini, M. Belakhovsky, A. I. Chumakov,
Phys. Rev. Lett. 82, 4847–4851 (1999).
9. M. Tegze, G. Faigel, S.Marchesini, M. Belakhovsky, O. Ulrich, Nature,
407, 38 (2000).
10. S. Marchesini, F. Schmithüsen, M. Tegze, G. Faigel, Y. Calvayrac,
M.
Belakhovsky, J. Chevrier, A.S. Simionovici, Phys. Rev. Lett. 85, 4723–4727,
(2000)
11. P. Korecki, J. Korecki, T. Slezak, Phys. Rev. Lett. 79, 3518, (1997)
| Természet Világa, | 132. évfolyam, 9. szám, 2001. szeptember
https://www.chemonet.hu/TermVil/ https://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez