Bódor Levente
Krúdy Gyula Gimnázium, Nyíregyháza
2000-ben ismét olimpiai játékokat rendeztek. A világ várakozással tekintett az események elé. Az újságok a lehetséges eredményeket taglalták. A hírek hatására bennem is felvetõdött a kérdés: mire is képes az ember? Ezért az 1896–2000 közötti idõszakot áttekintve több olyan olimpiai sportágban is megvizsgáltam az eredményeket, amelyek jól mérhetõk (vagyis a pontozásos sportágakkal nem foglalkoztam). Az eddigi olimpiai eredményekbõl táblázatot készítettem, és grafikonon ábrázoltam. Azt reméltem, hogy a grafikonok alapján közelítõleg meg tudom jósolni a várható teljesítményeket, de számításba vettem, hogy mindezt sok tényezõ befolyásolja (például környezeti hatások, doppingszerek); gyakran vannak kiugró rekordok is, amelyekbõl változatos függvénydiagram készíthetõ. Ezekre közelítõ függvények illeszthetõk, és így lehet hozzávetõleges adatokat meghatározni az elkövetkezõ néhány évre.
Az adatokat több forrásból gyûjtöttem, például A sport krónikája címû könyvbõl és az internetrõl az alábbi címekrõl:
www.ac.uk/cimt/data/olypics/olymindx.htm/;
www.hickoksports.com/history/olympix.shtml/;
abc.net.au/olympics_1996/sportspg.htm/;
www.usswim.org/olympics/olymedme.htm/.
A doppingszerekkel kapcsolatos információkat is az internetrõl szereztem:
www.ncaa.org/sports_sciences/drugtesting/banned_list.html;
www.coe.fr/eng/legaltxt/135e.htm;
www.ausport.gov.au/asda/;
www.endureplus.com/Doping.cfm;
sportsmedicine.about.com/health/sportsmedicine/msubdrugs.htm.
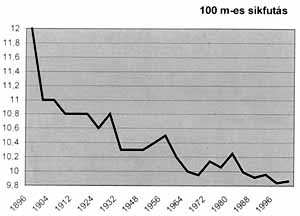
Olyan sportágakat választottam, amelyek eredményei jól mérhetõk: úszás, futás, távolugrás és magasugrás. E sportágak eredményeinek idõbeli alakulását az 1. táblázat, grafikonok formájában pedig az 1–6. ábra mutatja. Ez után jött a folyamat izgalmas része, megpróbáltam közelítõ függvényeket alkalmazni, hogy leírjam a 100 m-es síkfutás diagramját, amelyet Texas Instruments függvényrajzoló számológépem segítségével végeztem el. Ezt a gépet Hollandiában, az Ifjú Kutatók Nemzetközi Konferenciáján nyertem 2000 áprilisában a Természet Világa diákpályázatára beküldött munkámmal.
 |
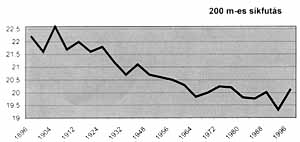 |
| 1. ábra | 2. ábra |
Az adatok elemzése
Az adatokat olyan koordinátarendszerben vettem fel, ahol az x tengely az idõ (olimpiák éve), az y tengely pedig a gyõztes idõ, vagy ugrási magasság, illetve hossz. Látható, hogy a grafikonokon csökkenés látható, ha nem is monoton módon, mely tény behatárolja, hogy milyen típusú függvénnyel próbáljuk meg leírni a grafikonokat. A lineáris függvény kezdetnek nem rossz, de az adatok azt mutatják, hogy az idõrekordok egyre lassuló mértékben csökkennek, azaz valamilyen hiperbolikus görbét sejtetnek. Már a harmadfokú egyenlet is jól ráillik a diagrammra, de egy idõ után óriási gyorsaságú fejlõdésnek kellene bekövetkeznie, ami nem valószínû. A legjobb talán a logaritmikus, vagy az exponenciális függvény. Az exponenciális egy bizonyos számhoz tart, amit a végtelenben ér el, de szerintem mindig lesz újabb ember, aki javít a meglévõ olimpiai rekordon. Az is lehet, hogy az emberiség eléri teljesítõképessége határát, és nem tud majd rekordot dönteni. Az mindenesetre bizonyos, hogy az idõeredmények csökkennek, a teljesítmények nõnek, méghozzá egyre kisebb mértékben.
Az eredmények javulásának okai
Az orvosi háttér egyre magasabb technológiával rendelkezik, és így kiválasztják a legmegfelelõbb versenyzõket. Fejlõdik az edzéstechnika és az ezekhez szükséges eszközök is.
Nõ a fizikai teljesítmény, mert nõ a testsúly, és fejlõdnek az emberi izmok.
A táplálék minõsége is javul, amivel kedvezõen befolyásolhatják a sportolók teljesítõképességét (például vitaminok használata).
 |
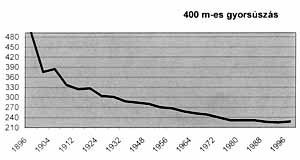 |
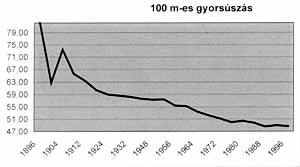
| 3. ábra | 4. ábra |
Doppingszerek alkalmazása: 1930-ban megjelenik az amfetamin, aminek eredménye szinte minden grafikonon látszik, ettõl kezdve egészen 1968-ig állandó teljesítménynövekedés érzékelhetõ. Az utóbbi évek eredményeiben némi visszaesés látható, ami annak tudható be, hogy javul a doppingellenõrzés.
Néhány érdekes megfigyelés a diagramok alapján
A vizsgált sportágakban láthatjuk, hogy az elsõ eredmények kiugróan rosszak, majd némi bizonytalansággal, de javulni kezdenek (meg kell jegyezni, hogy ekkor az úszóversenyeket még nyílt vízen rendezték). A harmadik olimpián, 1904-ben, minden rekord visszaesik. A magyarázat az lehet, hogy ezen az olimpián, amit az amerikai St. Louis-ban rendeztek, kevés külföldi résztvevõ volt, mivel nem tudták biztosítani az utazási feltételeket az európaiak számára. Csak a leggazdagabb országok küldhettek tehát versenyzõket korlátozott számban. A 100 és 400 m-es gyorsúszásnál 1904 után szinte monoton csökkenõ exponenciális függvénnyel írható le a diagram.
A futásnál a helyzet nem ilyen egyszerû, mert azt több tényezõ befolyásolja, mint az úszást. Ez a sport szabadtéri, tehát a versenyzõket befolyásolja a szél, a hõmérséklet és a napsugárzás, ugyanis a fénynek ritmusbeállító szerepe is van. Az úszók általában fedett térben úsztak/úsznak, közel állandó hõmérsékletû vízben. Ezért a futásnál és a szabadtéri játékoknál a grafikonoknak csak néhány rövidebb szakaszát elemezhetjük.
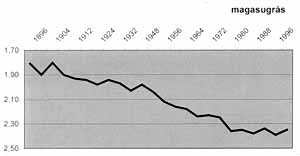
Az 1968-as mexikói olimpián különlegesen jó eredmények születtek, szinte minden addigi rekord megdõlt, ami a földrajzi elhelyezkedéssel függ össze. Mexikó 2000 méteres tengerszint feletti magasságával különleges feltételeket biztosított: kisebb a nehézségi gyorsulás, a légnyomás és a levegõ sûrûsége, mint a tengerszinthez közelebb. Talán ezért állíthatta föl Bob Beamon a távolugrás 8,9 méteres rekordját, amit máig sem döntöttek meg.
 |
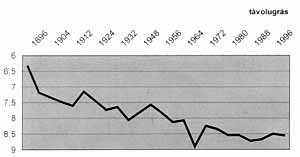 |
| 5. ábra | 6. ábra |
Az 1980-as moszkvai olimpián az Egyesült Államok nem vett részt, s talán ezért nem születtek újabb rekordok az amerikaiak által kedvelt atlétikai és úszósportágakban. A Los Angeles-i olimpia sem hozott óriási javulást, mert itt viszont az akkori szocialista országok nem jelentek meg.
1930-tól 1968-ig nagyon sok új rekord született, és nem sok visszaesést tapasztalhatunk, amit a doppingszerek megjelenésével magyarázhatunk. 1956 körül szinte minden grafikon egyenletes javulást mutat. E javulás az 1972-es olimpián változik meg, mert 1968-ban a NOB meghatározza a dopping fogalmát, és teszteket végeznek az olimpián, amelyek nagyon sok eltiltáshoz vezetnek. 1972-ben a versenyzõk már nem merik olyan mértékben használni a tiltott szereket. 1976, 1980 és 1988-ban a nõi úszás aranyérmesei szinte csak az akkori NDK-beli nõi versenyzõk. Egyes feltételezések szerint ezeket a nõket férfihormonokkal kezelték, ezért hangjuk mélyebb lett, izomzatuk átalakult, és borotválkozniuk kellett a híresztelések szerint.
Hipotézis felállítása
Megpróbáltam megjósolni az 1896-tól 1996-ig született eredmények alapján a 2000. évi olimpia eredményét a 100 m-es síkfutásban. Többféle közelítést is fölírtam számológépem segítségével:
lineáris: y = –1,558 695 6521 739 x + 12,683 195 652 174
másodfokú: y = 2,052 865 612 6483 x2 – 7,553 063 241 1069 x + 19,901 697 628 459
harmadfokú: y = –4,959 772 949 2656 x3 + 26,776 670
692 431 x2–
– 39,586 957 131 704 x + 31,340 207 436 686
negyedfokú: y = 13,329 957 708 355 x4 – 82,806 725
866 059 x3+
+ 191,648 826 088 37 x2 –196,896 520 786 66 x + 86,398 213
568 238
logaritmikus: y = 11,226 299 445 549 – 2,275 450 409 1458 ln(x)
exponenciális: y = 12,894 050 037 542 · 0,862 884 937 147 44x
Ezek közül az exponenciális függvény volt az, amely igazán jól ráillett a diagramra. Tehát ezzel próbáltam megjósolni a 2000. évi eredményt, ami meglepõen jól sikerült. Az eredmény ezzel a függvénnyel 9,8743 másodperc lett, ami szinte ugyanaz, mint a tényleges eredmény, ami 9,87 másodperc volt a sidneyi olimpián. Ha az eredményeket csak 1988-ig vettem figyelembe, és ezzel írtam föl a további eredményeket, akkor is közeli értékeket kaptam:
| becsült
eredmény |
tényleges
eredmény |
|
| 1992 | 9,924 s | 9,96 s |
| 1996 | 9,87 s | 9,84 s |
| 2000 | 9,8165 s | 9,87 s |
Az eddigi eredményekbõl sejthetõ, hogy valamilyen korlátnak kell lennie, ami behatárolja a teljesítõképességet. Az emberek sebessége egy bizonyos határig a fizikai méretükkel növekszik. Az izom nem képes nagyobb teljesítményre, mint amennyi a másodpercenkénti energia ellátása, ha az izomban rejlõ tartalékot nem vesszük figyelembe. Az izom teljesítménye arányos annak oxigén- és tápanyag-ellátottságával. Az energiatermelés ugyanis az oxigénnel elégetett tápanyag függvénye. A tápanyagot és az oxigént az áramló vér juttatja el az izomba, a vérellátás a szívmûködés függvénye.
A legújabb doppingszerekben egy újfajta fehérjét
használnak, ami növeli a vörösvértestek számát.
Így egyre több energia juthat az izmokba, és magasabb
teljesítmény elérésére lesznek képesek.
Ma már e szereket is ki tudják mutatni, így csak egy
esély maradhat a rekordok megdöntésére, mégpedig
a testsúlynövekedés. Ez utóbbi folyamatban van,
mert az emberek átlagmagassága és ezáltal testtömege
(az izomzat mennyisége) növekszik.
IRODALOM
A sport krónikája
Fizika az élõvilágban
www.ac.uk/cimt/data/olypics/olymindx.htm/;
www.hickoksports.com/history/olympix.shtml/;
abc.net.au/olympics_1996/sportspg.htm/;
www.usswim.org/olympics/olymedme.htm/;
www.ncaa.org/sports_sciences/drugtesting/banned_list.html;
www.coe.fr/eng/legaltxt/135e.htm;
www.ausport.gov.au/asda/;
www.endureplus.com/Doping.cfm;
sportsmedicine.about.com/health/sportsmedicine/msubdrugs.htm.
Az írás szerzõje Diákpályázatunkon a Varjú Dezsõ által kiírt Biokibernetika különdíj kategóriában I. díjat kapott.
1. táblázat. Olimpiai eredmények
| év | 100 m-es
síkfutás |
magas-
ugrás |
távol-
ugrás |
200 m-es
síkfutás |
100 m-es
gyorsúszás |
400 m-es
síkfutás |
| 1896 | 12 | 1,81 | 6,35 | – | 82,20 | 492,6 |
| 1900 | 11 | 1,9 | 7,185 | 22,2 | 62,80 | 376,2 |
| 1904 | 11 | 1,8 | 7,34 | 21,6 | 73,40 | 383,8 |
| 1908 | 10,8 | 1,9 | 7,48 | 22,6 | 65,60 | 336,8 |
| 1912 | 10,8 | 1,93 | 7,6 | 21,7 | 63,40 | 324,4 |
| 1920 | 10,8 | 1,94 | 7,15 | 22 | 60,40 | 326,8 |
| 1924 | 10,6 | 1,98 | 7,44 | 21,6 | 59 | 304,2 |
| 1928 | 10,8 | 1,94 | 7,73 | 21,8 | 58,6 | 301,6 |
| 1932 | 10,3 | 1,97 | 7,64 | 21,2 | 58,2 | 288,4 |
| 1936 | 10,3 | 2,03 | 8,06 | 20,7 | 57,6 | 284,5 |
| 1948 | 10,3 | 1,98 | 7,82 | 21,1 | 57,3 | 281 |
| 1952 | 10,4 | 2,04 | 7,57 | 20,7 | 57,4 | 270,7 |
| 1956 | 10,5 | 2,12 | 7,83 | 20,6 | 55,4 | 267,3 |
| 1960 | 10,2 | 2,16 | 8,12 | 20,5 | 55,2 | 258,3 |
| 1964 | 10 | 2,18 | 8,07 | 20,3 | 53,4 | 252,2 |
| 1968 | 9,95 | 2,24 | 8,9 | 19,83 | 52,2 | 249 |
| 1972 | 10,14 | 2,23 | 8,24 | 20 | 51,22 | 240,27 |
| 1976 | 10,06 | 2,25 | 8,35 | 20,23 | 49,99 | 231,93 |
| 1980 | 10,25 | 2,36 | 8,54 | 20,19 | 50,4 | 231,31 |
| 1984 | 9,99 | 2,35 | 8,54 | 19,8 | 49,8 | 231,23 |
| 1988 | 9,92 | 2,38 | 8,72 | 19,75 | 48,63 | 226,95 |
| 1992 | 9,96 | 2,34 | 8,67 | 20,01 | 49,02 | 225 |
| 1996 | 9,84 | 2,39 | 8,5 | 19,32 | 48,74 | 227,97 |
| Kiegészítés: | ||||||
| 2000 | 9,87 | 2,35 | 8,55 | 20,09 | – | – |
| Természet Világa, | 132. évfolyam, 11. szám, 2001.
november
https://www.chemonet.hu/TermVil/ https://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez