Kopházi Gergely
Jurisich Miklós Gimnázium, Kőszeg
Minden ősszel diákok serege népesíti be a nyáron ürességtől kongó iskolákat. A viszontlátás öröme határtalan. A boldog időszakot azonban hamarosan sötét felhők árnyékolják be. Jön az első matekdolgozat. Pedig a matematika tanulása nem csak tételek sokaságából vagy megoldhatatlannak látszó egyenletrendszerekből állhat. Érdekessé, izgalmassá, életszerűvé tehető néhány jó ötlettel. Ezt szolgálja egy kétnyelvű (magyar–angol) számítógépes program, mely egyedülálló módon ötvözi a történelmet, a kultúrát, a helytörténetet és a zenét a matematika tanulásával. Ugye, így már nem is olyan nehéz a matematika?„A matematika tárgya annyira komoly,
hogy hasznos minden alkalmat felhasználni arra,
hogy szórakoztatóbb formában foglalkozzunk vele.”
(Pascal)
A számítógépes program
Matematikaóráinkat színesebbé, érdekesebbé tehetjük, ha a tanórát városnéző barangolással kötjük össze, s egy-egy helyszínen mutatunk rá a matematikai összefüggésekre, melyeket az utcák, a terek és épületek szinte tálcán kínálnak. Így kapcsolatot teremthetünk a különböző tudományterületek között, és a számítógép segítségével szinte játszva tanulhatunk.
Középiskolás barátaimmal (Varga Zoltánnal és Szárnyas Gáborral) olyan CD-t készítettünk, amely Kőszeg városát, annak történelmét mutatja be, körséta segítségével, harmincegy látnivalóval. (Írásunkban ezekből tízet mutatunk be.) A CD-n minden helyszínhez részletes történelmi és művészettörténeti összefoglaló tartozik, számos, a nevezetességet ábrázoló fotóval. A város történelmének megismerése mellett matematikai ismereteinket is felfrissíthetjük, hiszen minden helyszínhez készíthető egy-egy érdekes matematikai feladvány is, melynek megoldása szintén megtalálható a CD-n. A matematikai feladatok az általános és középiskolai tananyaghoz kapcsolódnak, melyeket a város építészeti és művészeti értékeinek adatait felhasználva készítettünk. Többségük sík- vagy térgeometriai, de találkozhatunk egyenletekkel, kombinatorikai feladatokkal, sorozatokkal, halmazokkal is. Bolyongásunkat zenei aláfestés teheti hangulatossá. A zene, akárcsak a város, középkori hangulatot idéz. Választhatunk reneszánsz zenék és zongorajáték közül.
Virtuális túránk során, hogy el ne tévedjünk, térkép segít bennünket. Ezen többféle nagyításban láthatjuk Kőszeg belvárosát, a város festői szépségű alpokaljai környezetét. A megismerni kívánt helyszín a térképről egy kattintással elérhető, megkönnyítve a tájékozódást. Ha kellőképpen elfáradtunk, a galériában száznál is több fotón pihentethetjük szemünket. Amennyiben játszani támad kedvünk, kvízzel ellenőrizhetjük tudásunkat addig megszerzett kőszegi ismereteinkről.
A program HTML-nyelven íródott, ezért bárki megtekintheti egy webböngésző segítségével. A CD kétnyelvű, hogy az angolul beszélők is játszva tanulhassanak, könnyen megismerhessék környezetünket, kultúránkat, városunkat, és bepillanthassanak matematikai tanulmányainkba.
A kőszegi építészet és a matematika
A program bemutatása után nézzünk meg tíz kőszegi helyszínhez kapcsolódó feladatot.
1. feladat. A Jézus Szíve-templom (1. ábra) belső
díszítésein a következő mintát fedeztük fel:
 |
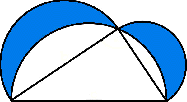 |
| 1. ábra. A Jézus
Szíve-templom |
Bizonyítsd be, hogy a két holdacska területe egyenlő a háromszög területével! (Ez a tétel egyébként Hippokratész holdacskái néven ismert.)
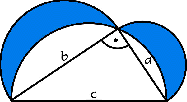
Megoldás. Mint láthatjuk, egy derékszögű háromszögről, a köré írt félkörről, és a befogók fölé írt félkörökről van szó. Legyen a háromszög két befogója a és b, átfogója c.
![]()
A teljes síkidom területe a háromszög területének és a két félkör területének az összege:
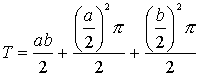
A holdacskák területe a teljes síkidom és a félkör területének a különbsége:

Mivel a háromszög derékszögű, alkalmazható rá Pitagorasz tétele, miszerint a2+b2=c2, ezért
![]()
Tehát a holdacskák területe egyenlő a háromszög területével.
k
2. feladat. Egy lány nyolc barátját szeretné meghívni piknikezni a Hétforráshoz (2. ábra), de csak négy számára van hely a kocsiban. Hányféle módon választhatja ki, hogy kiket visz magával, ha köztük van két testvér is, akiket nem szeretne elválasztani egymástól?

2. ábra. Hétforrás
Megoldás. A feladatban a nehézség az, hogy a testvéreket nem lehet egymástól elválasztani. Ha sorrendbe akarnánk rakni a lányokat, azt úgy oldanánk meg, hogy a két testvért egy személyként kezeljük. Ebben az esetben azonban ez nem célszerű, mivel kiválasztjuk a lányokat. Nem mondhatjuk, hogy 7 lány közül kell hármat kiválasztanunk, mert akkor előfordul, hogy tényleg csak hármat hív meg, ha a két nővér nincs bent e háromban.
A problémát ezért célszerű úgy megoldani, hogy két részre bontjuk.
a) Ha mindkét testvért beültetik az autóba, a 6 barát közül még 2 ülhet be. A lehetőségek száma:
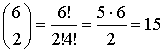
b) Ha nem a testvéreket ülteti be, a 4 vendéget a másik 6 barátból kell kiválasztania. A lehetőségek száma:
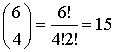
tehát ebben a sorrendben 30-féle variációban viheti magával barátait a lány.
Ha két fuvar sorrendjét felcseréljük, az összes lehetőségek száma 2·30=60.
k
3. feladat. A Lauringer-ház kovácsoltvas cégére (3. ábra) az egykori Heidenreich lakatosműhely egyik legszebb darabja. Tíz méterről az alját 26 fokos, a tetejét 30 fokos emelkedési szögben látjuk. Milyen magas a cégér?

Megoldás. Készítsünk vázlatot!
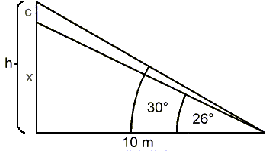
Használjuk a trigonometrikus szögfüggvényeket!
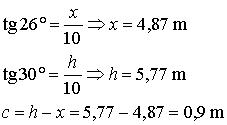
A cégér tehát 89 cm magas.
k
4. feladat. A vasútállomás és a Vasút a Gyermekekért Alapítvány (4. ábra) épületei 1 km-re vannak egymástól. A két épület között a műúton egy 1000 m-es kötelet feszítünk ki. A kötélbe egy 15 cm-es darabot toldunk. Ha a közepét megemeljük, mi fér át alatta: rovar, csiga, kutya, esetleg ember?

4. ábra. A Magyar Államvasutak Nevelő- és Diákotthona
Megoldás.

ABC egyenlő szárú háromszög, alapja dAB=1000 m, CT felezőmerőlegese AB-nek, ezért dAT=500 m.
dAC+dCB=1000,15 m, dAC=500,075 m.
Az ATC derékszögű háromszögre alkalmazva a Pitagorasz-tételt:
5002+d2TC=500,0752, ebből dTC=8,66 m.
Szinte hihetetlen, de ekkora betoldással 8,66 m-re lehet felemelni a kötél közepét, így akár egy ember is könnyedén átsétálhat alatta.
k
5. feladat. Futóversenyt rendeznek a Zwingertől (Öregtoronytól 5. ábra) az Óházig. A 10 km-es távolságot egy futó 1 óra alatt teszi meg. Ahol jó az út (egyenes, sík terepen), ott 14 km/h sebességgel halad, ahol rossz, ott 6 km/h sebességgel. Milyen hosszú a jó út?

5. ábra. Az Öregtorony
Megoldás. Tegyük fel, hogy x km a jó út hossza.
Ebből következik, hogy a dombon az út hossza (10–x) km.
A jó úton 14 km/h sebességgel halad, így az x km hosszú utat 14 km/h sebességgel x/14 óra alatt teszi meg.
A rossz úton a (10–x) km hosszú utat 6 km/h sebességgel (10–x)/6 óra alatt teszi meg.
A két időtartam összege 1 óra, ezért
A jó út tehát 7 km hosszú.3x+70–7x=4228=4x
x=7
k
6. feladat. A Patikamúzeum (6. ábra) legszebb bútordarabjának legfelső polcán 23 db tégely van, és minden további polcon az előzőnél 5-tel több. Hány tégely van a 8 polcon összesen?

6. ábra. A patikamúzeum
Megoldás. Az egyes polcokon sorakozó tégelyek száma számtani sorozatot alkot, amelynek első eleme a1=23, a különbsége d=5, a polcok száma n=8.

k
7. feladat. Az alábbi térképvázlat alapján kell eljutnunk a Kálvária-templomtól (7. ábra) a szállásunkig úgy, hogy közben a tanösvényt is érintsük! Milyen útvonalon haladjunk, hogy a legrövidebb utat tegyük meg, és mekkora ez az út?

7. ábra. A Kálvária-templom
|
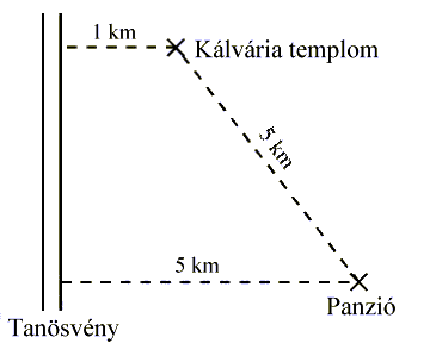 |
Megoldás. Mivel két pont között a legrövidebb távolság egy egyenesre
esik, gondolatban tükrözzük a tanösvény vonalára a Kálvária-templomot:
(Mivel KT=K’T, a legrövidebb út a
K’P szakasz lesz).
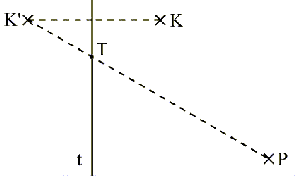
Keressünk derékszögű háromszögeket!

KOP derékszögű háromszögre alkalmazva Pitagorasz tételét: KO2+42=52.
Ebből KO=3 km, ezért K’O’=3 km.
KO’P’ derékszögű háromszögre alkalmazva Pitagorasz tételét: K’P2=K’O’2+O’P2, vagyis K’P2=32+62.
Így K’P»6,7 km.
A legrövidebb út 6,7 km.
k
8. feladat. Iskolánkban (8. ábra) 381 diák tanul. Valamennyien tanulnak angolt, németet, vagy mindkettőt. 311 diák tanul angolt, 223 diák németet. Hányan tanulják mindkét nyelvet?

8. ábra. A Jurisich Miklós Gimnázium Kőszegen
Megoldás. Szemléltessük a megoldást Venn-diagrammal!
Angolt tanulnak azok, akik csak angolt, vagy mindkét nyelvet tanulnak, németet pedig, akik csak németet, vagy mindkét nyelvet tanulják.
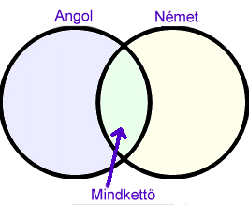
A két nyelvet tanuló diákok számának összege a csak angolt, a csak németet, és 2-szer a mindkét nyelvet tanulók számát adja.
Ha tehát ebből az összegből kivonjuk a tanulók létszámát, megkapjuk
a mindkét nyelvet tanulók számát, vagyis (311+223)–381= =153. Tehát 153
diák tanulja mindkét nyelvet.
k
9. feladat. A Dunántúl legmagasabb pontján áll az Írottkő-kilátó
(9. ábra). Meg akarjuk mérni a magasságát. P és Q pontból, amelyek
a kilátó aljával egy egyenesben vannak, és egymástól 10 m távolságra helyezkednek
el, megmérjük, mekkora emelkedési szögben látszik a kilátó teteje. E szögek
22, illetve 32 fokosak. Milyen magas a kilátó, ha az ember, aki méri, 180
cm magas?

9. ábra. Írottkő
Megoldás. Először egy jó ábrát kell készítenünk a feladatról,
amely a további megoldásban segít.
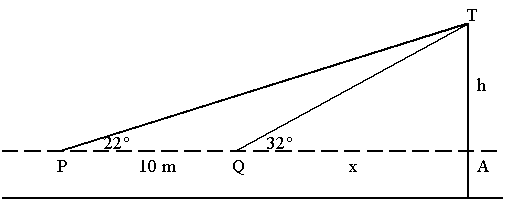
Az ábrán két háromszög látható. Mindkettő derékszögű. Mire is emlékeztet minket a derékszögű háromszög?
A) Thalész-tétel B) Pitagorasz-tétel C) szögfüggvények
Jelen esetben a szögeket ismerjük, így szögfüggvényeket kell használnunk. Tudunk valamit a szögek mellett fekvő befogókról, és keressük a szöggel szemközti oldalt. Így a tangens vagy kotangens szögfüggvényeketet kell használnunk. Jelöljük a kilátó magasságát h-val, és a kilátótól az első távolságot x-szel, mindkettőt méterben értve.
A QAT derékszögű háromszögből:
tg32o=h/x
A PAT derékszögű háromszögből:
tg22o=h/(x+10)
Két egyenletünk és két ismeretlenünk van, így meg is tudjuk oldani az egyenletrendszert:

h=11,43 m.
Figyelembe véve a mérő szemmagasságát is, a kilátó 9,73 m magas.
k
10. feladat. Milyen hosszúak a Szent Imre-templom (10. ábra) óramutatói, ha végpontjaik 2 órakor 52 cm-nyire, 9 órakor 68 cm-nyire vannak egymástól?

10. ábra. Szent Imre-templom



Tehát az óra mutatói 32 és 60 cm-esek.
k
Hasonló érdekes matematikai barangolásokat bárki könnyen készíthet lakóhelye környékén. Sok sikert hozzá.
Az írás szerzője Diákpályázatunkon a Martin Gardner által kiírt Matematika különdíj kategóriában II. díjat kapott.
| Természet Világa, | 133. évfolyam, 8. szám, 2002. augusztus
https://www.chemonet.hu/TermVil/ https://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez