Bolyai János forradalma
Második rész
A Bolyai–Lobacsevszkij-geometria előzményei
A
geometria szó az ógörög geometrein szóból ered, mely földmérést jelent.
Az ókori geometria kezdetben egyszerű szabályok gyűjteménye volt, melyhez
kísérletezés, adatgyűjtés és intuíció révén jutottak. Egyiptomban, Babilonban,
Kínában stb. egyaránt léteztek ilyen ismeretek, ám a görögök voltak az
elsők, akik geometriai állításokat deduktív úton vezettek le ismert, vagy
nyilvánvalónak tartott állításokból. Közöttük is a milétoszi Thalész volt
az első, aki a bizonyítás módszerét alkalmazta annak eldöntésére, hogy
mely állítás igaz, illetve hamis. Ennek kapcsán létrehozta az első logikus
geometriát. A rendszerező munkában őt Püthagorasz, a misztikus vallási
szekta alapítója és a róla elnevezett tétel felfedezője követte.
Kr. e. 400 körül a matematikus (nem az orvos) Hippokratész összefoglalta a püthagoreusok ismereteit a sík geometriájáról. A mű az Elemek címet kapta. Bár ez nem maradt fenn, mégis valószínű, hogy Eukleidész első négy könyve ezen alapult.
Kr. e. 387-ben az athéni városkaputól mintegy másfél kilométer távolságra Platón megalapította híres iskoláját. Minthogy a terület, melyen az iskola elhelyezkedett, egykor Akadémosz tulajdona volt, és már az iskola megalapítása előtt az Akadémia nevet viselte, ez lett az iskola neve is. Platón Akadémiáján intenzív matematikai oktatás folyt, melyről igen jó összefoglaló képet ad Fowler (1999) könyve. Ennek az iskolának volt tanítványa Eukleidész, aki Kr. e. 300 körül kiadta az Elemek című, tizenhárom kötetes könyvét. Tudománytörténészek kimutatták, hogy az Elemek jelentős mértékben támaszkodik más, korábbi könyvekre, nevezetesen Architász, Eudokszusz és Theaitetosz könyveire.
Eukleidész Elemekje olyan mestermű, mely kétezer éven át forrása volt a geometriai ismereteknek. Legnagyobb érdeme, hogy ezeket egységes logikai rendszerbe foglalta, melyben kevés számú adott állításból, logikusan, egymásra épülve következnek az újabb és újabb állítások, deduktív bizonyítás útján. A kiindulást jelentő viszonylag kevés számú állítás egy része posztulátum, követelmény, más része pedig egyszerű állítás, axióma. Egyes kommentátorok azt állítják, hogy a posztulátum nem egyéb, mint feltevés, kiindulópont, melyet önkényesen választunk, és így igaz voltának kérdése nem vetődik fel, míg az axióma olyan állítás, mely mindenki számára nyilvánvaló. Mások szerint az Elemekben a posztulátumok inkább geometriai jellegűek, az axiómák pedig inkább univerzálisak. A mai tárgyalásban nem szokás különbséget tenni a kettő között, és valamennyi kiinduló állítást axiómának nevezünk. Ez a szokás tulajdonképpen már régi.
Az V. euklideszi posztulátum, a különböző geometriák kiindulópontja, Bolyai Jánosnál XI. axiómaként jelentkezik. A történelem folyamán az Elemek több kiadást ért meg, egyesekhez hozzá is adtak. A továbbiakban tehát, ha V. posztulátumról vagy XI. axiómáról írunk, ezen ugyanazt értjük.
Az Elemekben az axiómákon kívül vannak definíciók és tételek. Eukleidész definiálja a pont és az egyenes fogalmát: „Pont” az, aminek nincs része, „egyenes” pedig a kiterjedés nélküli hosszúság. Mai axiómarendszerünkben ezek nem definiált fogalmak, hiszen csak az objektumok egymással való kapcsolatát foglaljuk rendszerbe, az objektumok mibenlétét szabadon hagyjuk. Eukleidész bebizonyítja pl. azt, hogy a háromszög szögeinek összege 180°, azaz a+b+g=180°, de ezt az egyenletet nem írja fel, hanem úgy fogalmaz, hogy a szögek összege két derékszög. Sem a + jel, sem a fok jele ekkor még nem volt használatban. Bebizonyítja Püthagorasz tételét: a2+b2=c2, de ezt is másképpen fejezi ki, mégpedig a derékszögű háromszög oldalaira helyezett négyzetek területével. A nagy számú tétel bizonyítása során azonban olyan gondolatmeneteket is alkalmaz, melyek mai szemmel kifogásolhatók. Ebben szerepet játszik az is, hogy a geometria axiómarendszere az Elemekben még nem teljes. A mai egzaktsági igényünknek megfelelő axiómarendszert 1899-ben David Hilbert (1862–1945) fogalmazta meg. Bolyai, Lobacsevszkij és Gauss még az Elemek axiómarendszerén belül gondolkodott. Ez azonban nem jelenti azt, hogy tételeik érvényüket vesztették. Csupán arról van szó, hogy a régi tételeket ma az új keretek közé kell helyeznünk, és a mai diáknak (az egyébként igaz állítás) bizonyítását másképp kell tanítanunk. Pl. Bolyai idejében még a szemléletre hagyatkoztak, amikor arról volt szó, hogy egy egyenesen a C pont az A és B pontok között van, Hilbertnél a rendezés fogalma is axiomatikus megfogalmazású.
Hilbert axiómáit öt csoportba soroljuk, ezek a következők: (1) illeszkedési, (2) rendezési, (3) egybevágósági, (4) párhuzamossági és (5) folytonossági axiómák. Az utolsó előtti csoportba csupán egy axióma tartozik, melyet ebben a formában először John Playfair (1748–1819) fogalmazott meg.
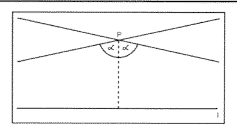
Playfair párhuzamossági axiómája: minden l egyeneshez és egy rajta kívül fekvő P ponthoz legfeljebb egy olyan egyenes létezik, mely ezt a pontot tartalmazza és l-hez párhuzamos.
A fenti axiómák együttesen értelmezik az euklideszi geometriát. Playfair axiómájában a „legfeljebb egy olyan egyenes létezik” megfogalmazás kicserélhető azzal, hogy „pontosan egy olyan egyenes létezik”. Az ugyanis a többi axiómából bizonyítható, hogy létezik legalább egy a kívánalmaknak megfelelő egyenes.
A párhuzamossági axióma, Eukleidésznél az V. posztulátum, eredeti formája más. Eukleidész előbb értelmezi a párhuzamos egyenesek fogalmát: egy síkban vannak, és ha mindkét irányba meghosszabbítjuk ezeket a végtelenségig, nem metszik egymást. Ezt követően bebizonyítja, hogy ha az egyenesnek egy transzverzális egyenessel bezárt megfelelő szögei egyenlők, akkor ezek párhuzamosak. A fordított állítás bizonyításához megfogalmazza és felhasználja az alábbit.
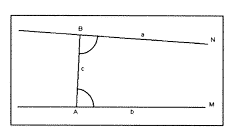
Eukleidész V. posztulátuma: ha két egyenest metsz egy harmadik, és a keletkezett, ugyanazon az oldalon lévő belső szögek összege kisebb, mint két derékszög, akkor ezek az egyenesek a végtelenbe meghosszabbítva metszik egymást.
Hilbert axiómarendszerének legkézenfekvőbb modellje a síkgeometria. Ha nem akarunk a szemléletes pontokkal és egyenesekkel dolgozni, akkor gondolhatunk Descartes analitikus geometriájára, ahol ezek számokkal, ill. számhalmazokkal vannak megadva: egy pont egy (x, y) számpár, egy egyenes pedig azoknak az (x, y) számpároknak a halmaza, melyek eleget tesznek egy y=ax+b egyenletnek, ahol a és b rögzített valós számok. Most azonban ezek az objektumok nem a vizuális pontokat és egyeneseket adják meg analitikusan (mint Descartes-nál), hanem ők maguk jelentik a pontokat, illetve az egyeneseket. Hasonló módon kapjuk az (x, y, z) számhármasok összességén belül a térgeometriát, a rendezett szám n-esek pedig elvezetnek a többdimenziós euklideszi geometriához.
Az V. posztulátum abban különbözik az első négytől, hogy nem tudjuk tapasztalati úton ellenőrizni. Csak egyenes szakaszokat tudunk megrajzolni, végtelenbe nyúló egyeneseket nem. A történelem folyamán, egészen Bolyai, Lobacsevszkij és Gauss koráig, e posztulátumot az elmélet szépséghibájának tartották és erős volt a hiedelem, hogy ez a többi axiómából bizonyítható. Bonola (1911) és Stäckel (1914) jó összefoglalást nyújt a párhuzamossági axióma különféle megfogalmazásairól, melyek a történelem folyamán előfordultak, és annak bizonyítási kísérleteiről. Mi ezzel csak röviden foglalkozunk.
Proklusz (Kr. u. 410–485) kommentárokat írt Eukleidész első könyvéhez, és ezekben tesz említést a korai bizonyítási kísérletekről. Ptolemaioszt (Kr. u. II. század) említi, többek között, bizonyítási kísérletét megbírálja, ám maga is elkövet egy hibásat. Az arabok, akik a matematikai felfedezések tekintetében a görögök művét folytatták, szintén foglalkoztak az V. posztulátummal. Al-Nirizi (Kr. u. IX. század) kommentárokat írt Eukleidész első könyvéhez, Naszir Eddin (1201–1279) pedig a következő szellemes átfogalmazását adta az V. posztulátumnak: ha egy görbe minden pontja egyenlő távolságra van egy adott egyenestől, akkor ez a görbe maga is egyenes.
Nyugat-Európában az arab tankönyvek révén vált ismertté az Elemek, ezeket a XII. és a XIII. században lefordították latinra. Később, a XV. és a XVI. században megjelentek az eredeti görög szöveg alapján készített fordítások. A XVI. századtól a XVIII. század elejéig F. Commandino (1509–1575), C. S. Clavio (1537–1612), P. A. Cataldi (?–1626), G. A. Borelli (1608–1679), G. Vitale (1633–1711) és J. Wallis (1616–1703) voltak a legfontosabb matematikusok, akik az V. posztulátummal foglalkoztak, átfogalmazták, bizonyítását megkísérelték, a nem euklideszi geometria felfedezésének közvetlen előzményei előtt.
Az említett nyugat-európaiak közül Wallis eredménye a legérdekesebb. Feltételezve, hogy adott háromszöghöz tetszőleges méretű hasonló háromszögek (megfelelő szögeik egyenlők, de megfelelő oldalaik hosszúságai különbözőek) léteznek, levezette az V. posztulátumot. Itt felsejlik a Bolyai–Lobacsevszkij-geometria egy érdekes állítása: e geometrián belül egy háromszög mérete hasonlósági transzformációval nem növelhető, vagy csökkenthető. Nem lehet a háromszöget sem összehúzni, sem tágítani a szögek megtartása mellett. A hasonlósági transzformáció deformációt is eredményez.
A hiperbolikus geometria történetével foglalkozók körében megoszlanak a vélemények a tekintetben, hogy kik annak megalkotói és kik az előfutárok. Nem a Bolyai és Lobacsevszkij javára történő részrehajlás vezet, hanem csupán a matematikatörténetben alkalmazott normák elfogadása, amikor az alábbi megállapítást teszem: az újkori előfutároknak két csoportja van, a felfedezőknek egy, az alábbiak szerint. Az előfutárok első csoportjába tartoznak: Saccheri, Lambert, Legendre és Bolyai Farkas. Az előfutárok második csoportjába: Schweikart, Taurinus és Gauss. Felfedezők: Bolyai és Lobacsevszkij.
Ez csupán annyiban különbözik Stäckel és Engel (1895) klasszikus csoportosításától, hogy Gausst az előfutárok, és nem a felfedezők közé számítjuk.
Vannak más vélemények is, [l. pl. Bonola (1911), Gray (1979), Kline (1990)]. Bonola a felfedezők két csoportját különbözteti meg. Első csoport: Schweikart, Taurinus, Gauss, a második csoport: Bolyai, Lobacsevszkij. Gray a Riemann-geometriáig bezárólag vizsgálja a fejlődést, így szempontjai eleve mások. Kline egyébként nagyon informatív könyve Bolyai és Lobacsevszkij vonatkozásában felületes.
Bonola véleményével kapcsolatban elmondhatjuk, hogy ha Schweikart, Taurinus és Gauss a felfedezők közé soroltatnának, akkor ehhez a normához kellene igazítani a többi nagy matematikai felfedezés történetének a leírását is. Ebben az esetben pl. a diffenciál- és integrálszámítás felfedezői nemcsak Newton és Leibniz lennének, hanem legalábbis még Kepler, Galilei, Cavalieri, Saint-Vincent, Roberval, Fermat, Toricelli, Descartes, Wallis, Barrow, Child és mások, az újkorban. Még sok, hasonlóan fontos matematikus nevét említhetnénk egész Arkhimédészig visszamenőleg.
Az alábbiakban felvázoljuk az előfutárok idevágó eredményeit és megindokoljuk véleményünket.
Gerolamo Saccheri (1667–1733) olasz jezsuita matematikus két művet tett közzé, az egyikben (1733) az V. posztulátum bizonyításával foglalkozott, a másikban (1697) viszont lényegében kiépített egy nemeuklideszi geometriát, amelyben adott egyeneshez egy rajta kívül fekvő ponton átmenő párhuzamos egyenes nem létezik. Ebben a műben is bizonyítani akarta az V. posztulátumot, indirekt úton, ámde ahelyett, hogy ellentmondásra jutott volna, megalapozta az elliptikus geometriát (mai szóhasználattal élve). Saccheri kiindulópontja egy négyszög, melynek alapján álló két oldal egyenlő hosszúságú és mindkettő az alappal derékszöget zár be. Mármost az alappal szemben lévő oldal az előbb említettekkel azonos nagyságú szögeket zár be, melyek lehetnek derékszögek, tompaszögek, vagy hegyesszögek. Ezeket hipotéziseknek tekintve Saccheri bebizonyítja, hogy ha egy négyszögre valamelyik hipotézis a három közül érvényes, akkor valamennyi négyszög esetére érvényes ugyanez a hipotézis. Ebből viszont következik, hogy ha egy háromszögben a szögek összege egyenlő két derékszög összegével, vagy annál nagyobb, ill. kisebb, akkor ez minden háromszögre ugyanúgy érvényes. Ez az eredmény az abszolút (V. posztulátum, vagy ellenkezője nélküli) geometria fontos és szép tétele, később alapja lett Bolyai és Lobacsevszkij területszámítási tételeinek. Saccheri azonban az 1733-ban megjelent könyve végén ad egy hamis bizonyítást az V. posztulátumra, mely mintegy konklúziója addigi vizsgálatainak. Tóth Imre (2000) úgy vélekedik, hogy Saccheri ezt az inkvizíciótól való félelmében tette, mert az általa közölt hamis bizonyítás átlátszóan leegyszerűsített.
Johann Heinrich Lambert (1728–1777) svájci származású matematikus és filozófus élete nagy részét Berlinben töltötte. A párhuzamosokról írt műve halála után jelent meg. Saccherihez hasonlóan, Lambert is egy négyzetet vett alapul, melynek azonban három szöge volt derékszög, a negyedik pedig a három lehetőség mindegyike. Ennek alapján beszél ő is három hipotézisről: hegyesszög, tompaszög, derékszög.
Lambert egyik legfontosabb eredménye a geometriai alakzatok mértékével kapcsolatos. Az euklideszi geometriában a hosszúság, terület, köbtartalom külön-külön additív mértékeket jelentenek. Ezen azt értjük, hogy egymás mellé helyezett szakaszok (ill. síkbeli, vagy térbeli alakzatok) egyesítésének hossza (területe, köbtartalma) az egyes hosszúságok (területek, köbtartalmak) összege. A mértéket bonyolultabb ponthalmazokra is ki tudjuk terjeszteni az additivitás megtartásával. A hosszúságból, területből, köbtartalomból ilyen értelemben nyert mértéket mai szóhasználattal Lebesgue-mértéknek nevezzük. Nos, az euklideszi geometriában értelmezhetők olyan, az additivitás tulajdonságával rendelkező mértékek, melyek különböznek a Lebesgue-mértéktől. Lambert felfedezte, miszerint a hegyesszög hipotézise (melyet úgy is megfogalmazhatunk, hogy a háromszög szögeinek összege kisebb, mint két derékszög) esetén a geometriai mérőszámok nem választhatók meg tetszőlegesen, hanem azok – eltekintve egy univerzális pozitív szorzótól – egyértelműen adottak. Lambert közölt is erre egy elnagyolt bizonyítást.
Felfedezte továbbá, hogy a hegyesszög hipotézise esetén a háromszög területét a gömbháromszögtan egyik formulájából pusztán formális manipulációval megkaphatjuk. Ha egy gömbháromszög szögei a, b, g, akkor a gömbháromszög területe r2 (a+b+g–p), ahol r a gömb sugara. Az r sugár helyébe ir-et helyettesítve (ahol i az imaginárius egység) az előbbi formula átalakul az r2(p–a–b–g) formulává. Ha egy háromszöget kirakunk kisebb háromszögekből, akkor a nagy háromszögre vonatkoztatott előbbi formula egyenlő lesz a kis háromszögekre vonatkoztatott megfelelő formulák összegével. A mérték egyértelműsége miatt a fenti képlet megadja a háromszög területét a hiperbolikus geometriában (mai szóhasználattal élve), egy univerzális pozitív szorzótól eltekintve. A mérték ezután kiterjeszthető olyan halmazokra is, melyek háromszögek egyesítéseként adódnak. A fenti gondolatmenet világosabb kifejtése annak, ami Lambertnél olvasható. Lambert tulajdonképpen még az r2 (p–a–b–g) formulát sem írta fel. Másfelől a fenti eredményt abszurdnak tartotta, mert képzetes sugarú kör a geometriában nem létezik, és úgy vélte, hogy a hegyesszög-hipotézis abszurd következményei az V. posztulátum bizonyítását jelentik.
Legendre (1752–1833) egyik fő érdeme, hogy egy kitűnő geometriai tankönyvet írt, ez volt az első komoly riválisa az Elemeknek kétezer év óta. Tárgyunk szempontjából azonban azt kell megemlítenünk, hogy Legendre is felfedezte azt a tételt, amit Saccherivel kapcsolatban említettünk, így az a Saccheri–Legendre-tétel nevet viseli.
Bolyai Farkas (1775–1856) fiatalkorában intenzíven kísérletezett az V. posztulátum bizonyításával. Fő műve a Tentamen, melyben összefoglalta azokat a hipotéziseket, amelyeket az V. posztulátummal egyenértékűnek talált. Ezek közül az alábbi kettő a legérdekesebb.
– Négy pont, melyek nincsenek egy síkon, egy gömbön vannak.
– Három pont, melyek nincsenek egy egyenesen, egy körön vannak.
Ha a kettő közül akármelyik levezethető, akkor az V. posztulátum is levezethető.
Az előfutárok második csoportjában elsőként a marburgi jogászprofesszor, Schweikart (1780–1859) munkáját említjük. Egy marburgi matematikus, Gerling, közvetítésével 1818-ban elküldött Gaussnak egy rövid kéziratot, melyben a legfontosabb az, hogy egy az euklideszitől különböző „asztrál geometriát” lehetségesnek tart. Gauss a következő évben írt válasza ebben az esetben sem volt kedvező. Válaszában Gauss megemlíti (bizonyítás nélkül), hogy az asztrál geometriában, amikor adott egyeneshez egy rajta kívül fekvő ponton át egynél több párhuzamos egyenes húzható, a háromszögek területének felső határa
pC2 / [log=(1+Ö2)]2 ,
ahol C univerzális állandó. Mai tudásunk szerint ez a felső határ akkor éretik el, amikor a három oldal mindegyik párja egymáshoz képest aszimptotikus (elpattanó, magyarázatát ld. később). Nem világos Gaussnál az, hogy képletében log helyett log.hyp. szerepel.
Taurinus (1794–1874) megtalálta az összefüggést a C és a háromszög területében szereplő k állandó között:
k= C/log (1+Ö2)
Ezt 1826-ban megjelent könyvében publikálta. Taurinus elég messzire eljutott, többek között trigonometriai formulákat is levezetett a hegyesszög hipotézise esetére. Mindamellett az új geometriát nem fogadta el a fizikai értelemben vett tér lehetséges geometriájaként.
Kicsit részletesebben foglalkozunk Gauss idevágó munkásságával. Gauss semmit sem publikált a nemeuklideszi geometriáról. Eredményeit hagyatékából és a másokhoz intézett leveleiből lehet rekonstruálni. E téren nagyrészt Szénássy Barna (1977/1980) alapvető cikkére támaszkodunk.
Mindenekelőtt érdemes felfigyelnünk arra a jelenségre, hogy a XIX. század második felében Bolyai személye (igazságtalanul) háttérbe szorult Lobacsevszkijéhez képest. A XX. század elejére a kép kezdett tisztulni, legalábbis az európai kontinensen. Újabban azonban, a Gauss születésének 200. évfordulója alkalmából rendezett konferencia és az ebből az alkalomból megírt sok tanulmány hatására, Bolyai és Lobacsevszkij is Gausshoz képest gyakran háttérbe szorul. Sokan Gausst tartják a nemeuklideszi geometria igazi felfedezőjének.
Gauss, akit a matematikusok fejedelmének neveznek, valóban óriás az óriások között is. Nemcsak matematikus, hanem csillagász, fizikus és geodéta is volt. Munkássága a tiszta elmélet és az alkalmazás terén egyaránt alapvető. Összegyűjtött művei tizenkét hatalmas kötetet töltenek meg. Sartorius von Waltershausen, Gauss első életírója azonban megállapította, hogy Gausst különösebben nem érdekelte olyan geometria kidolgozása, mely az euklideszitől különböző. Más vélemény szerint is a három a betűs tudomány: az aritmetika, az analízis és az algebra érdekelte elsősorban.
Gauss hagyatékában 25–26 olyan helyet találunk, ahol a geometria alapjairól, illetve a nemeuklideszi geometriáról van szó, ám feljegyzései összesen 10–12 oldalt töltenének meg. Ezen kívül az 1796. március 30-tól 1814. július 9-ig vezetett naplójában találunk egy bejegyzést, amely egy mondatból áll: „A geometria alapjaiban kitűnő előrehaladást értünk el. Braunschweig, Sept. 1799”.
Gauss feljegyzései arról tanúskodnak, hogy alaposan ismerte Lambert (1786) könyvét. Ma már azt is tudjuk, hogy ezt 1795-ben, göttingeni tanulmányai első évében és 1797-ben is kikölcsönözte az egyetem könyvtárából (Dunnington, 1955). Gauss megfogalmazta a párhuzamos egyenesek fogalmát, mely kétségtelenül hasonló a Bolyai- és a Lobacsevszkij-féle párhuzamossághoz. Az 1819-ben Gerlinghez (valójában Schweikarthoz) írt válaszában bizonyítás nélkül megadta a hiperbolikus geometriai háromszög területének a felső határát (ezt már említettük). Az 1831. július 12-én Schumacherhez írott levelében közli a hiperbolikus geometriai kör kerületét, de nem bizonyítja, hanem egyszerűen nyeri az r sugarú gömbi kör kerületének a formulájából r helyébe ir-et helyettesítve. Az 1832. február 14-én (az Appendixre reagáló) Bolyai Farkashoz intézett levelében levezeti a hiperbolikus geometria háromszögének területi képletét. Ez Gauss legterjedelmesebb írása a nemeuklideszi geometriáról, ám bizonyítása nem teljes, mert felhasználja azt, hogy a háromszög maximális területe véges. Végül, 1840–1846 között megjegyzéseket fűz Lobacsevszkij (1840) könyvéhez. Ezek értékes észrevételek, de támaszkodnak az Appendix egyes összefüggéseire.
Az Appendix (először különlenyomatként jelent meg 1831 áprilisában) előtti időből tehát kevés eredményt lehet Gaussnak tulajdonítani, legalábbis dokumentálható módon.
Érdemes viszont felfigyelni arra, hogy Gauss ismerte Lambert könyvét. Bolyai János egyik írásából (l. Stäckel, 1914, 221–223. old.) viszont tudjuk, hogy mely matematikusok írásait ismerte ő a párhuzamosok elméletének köréből, és Lambert nincs közöttük. Eszerint vagy Gauss nem tett említést Bolyai Farkasnak Lambert könyvének létezéséről, vagy az apa nem mondta ezt el fiának. Az utóbbi esetet, Bolyai Farkas jellemét, fia iránt érzett apai szeretetét ismerve, kizárhatjuk. Akkor viszont arra következtethetünk, hogy Gauss egyáltalán nem volt közlékeny Bolyai Farkas irányában a párhuzamosok kérdését illetően. Ez azért fontos, mert több régebbi szerző állítja, hogy Bolyai János azt publikálta, amit apja Gausstól hallott. Ennek cáfolására egyéb érvek egész sora is felvonultatható. (l. Szénássy említett cikkének további részleteit és Császár (1978) cikkét).
B
relációval juttatjuk kifejezésre (Bolyai János jelölése). Ez a reláció
független az V. posztulátumtól, az abszolút geometria körébe tartozik és
rendelkezik a reflexív, szimmetrikus és tranzitív tulajdonságokkal: A