Püthagorasz, Rényi és a lemmingek,
avagy a káosz irracionalitása
Második rész
Diszkrét rágcsálók
Az irracionális számok rövid története
Írásunk első részében bemutattuk az irracionális számok megismerésével kapcsolatos alapvető matematikai és filozófiai jellegű problémákat, valamint azt, hogy ezek miként kapcsolódnak a kaotikus dinamikai rendszerekhez. Ezeket a gondolatokat most nagyon röviden összefoglaljuk.
Az irracionális számok létére először a pitagoreusok következtettek. Ez az új fogalom azonban annyira ellentétes volt világképükkel, hogy felfedezőjét megölték, és megtiltották, hogy bárki beszéljen az új típusú számokról. Első pillantásra talán furcsa ez a heves reakció, mégis érthetőbbé válik, ha meggondoljuk, hogy egyetlen irracionális szám végtelen mennyiségű információval írható csak le. Jogosnak tűnhet tehát a XX. századi intuicionisták megközelítése, akik szerint más módon tekinthetők létezőnek a racionális és az irracionális számok. Míg az előbbiek „statikus” értelemben léteznek, az utóbbiakat csak mint egy végtelen, soha be nem fejeződő folyamatot képzelhetjük el. Ha az irracionális számokat a racionálisokkal azonos módon létező objektumoknak fogjuk fel, akkor gödeli értelemben feloldhatatlan (vagyis egyszerre bizonyíthatatlan és cáfolhatatlan) állításokhoz juthatunk.
Rényi Alfréd mutatott rá elsőként, hogy az irracionális számok nem csupán a formálisan eldönthetetlen kérdésekkel, hanem a véletlennel is szoros kapcsolatban állnak. Cikkünk előző részében részletesen elemeztük a Rényi által is vizsgált,
xi+1 = 2 xi mod 1
(úgynevezett diadikus) rekurzióval megadott sorozatot, mely véletlen jellegű tulajdonságot mutat, ha az x0 kezdőérték irracionális szám. Rényi olyan determinisztikus rendszerre mutatott itt példát, melynek hosszú távú viselkedése megjósolhatatlan. Az ilyen rendszereket nevezzük kaotikusnak. A cikk első részében a kaotikus dinamika és az irracionális számok kapcsolatát firtattuk, most azonban azt fogjuk vizsgálni, hogy valóságos, kézzel fogható rendszerekben felléphet-e kaotikus viselkedés. Első példánkban egy különös rágcsálóval ismerkedünk meg.
A lemmingek titokzatos élete
Brehm (Brehm, 1990.) szerint a lemmingek (Lemmus lemmus) Skandinávia legrejtélyesebb állatai. Az egérhez hasonló kis rágcsálók hosszú időszakokra eltűnnek, majd hirtelen ellepik a környéket. Olaus Wornius 1633-ban könyvet írt róluk, s azt igyekezett bizonyítani, hogy a felhőkből hullanak alá, és ráolvasással sem lehet őket elűzni. Nem kíséreljük meg, hogy megmagyarázzuk a lemmingek titokzatos viselkedését, csupán egy rendkívül egyszerű, kvalitatív modell segítségével próbáljuk meg bemutatni, hogy milyen populációdinamika állhat esetleg a jelenség mögött. Tételezzük fel, hogy a lemmingpopuláció azonos időnként megduplázódik, viszont ha elér vagy túllép egy rögzített N küszöbszámot, akkor N lemming elpusztul, a többi elvándorol, és a korábbi szabály szerint tovább szaporodik. A küszöbszámot indokolhatja a lemmingek adott környezetében fellelhető táplálék mennyisége. Képletbe foglalva a lemmingpopulációt szabályozó törvényt rekurzióhoz jutunk, mely az i-edik állapotban mérhető Xi létszám függvényeként adja meg az (i+1)-edik állapot Xi+1 létszámát:
Xi+1 = 2 Xi mod N.
Láthatjuk, hogy mindössze az xi=Xi/N transzformációt kell végrehajtanunk, és máris a diadikus leképezéshez érkeztünk. Az utóbbit már részletesen tárgyaltuk, felmerül tehát a kérdés, hogy mit tudunk mondani Rényi eredményei alapján egy nagy létszámú lemmingpopuláció hosszú távú viselkedéséről. Másként fogalmazva: milyen statisztikát kapunk, ha véletlenszerű időpontokban megszámoljuk a lemmingeket (nagy N küszöbszámot feltételezve)? Vajon nagy N esetén a diadikus leképezés irracionális kezdőértékből induló trajektóriáira jellemző, determinisztikus, de megjósolhatatlan, ergodikus viselkedést vagy jól megjósolható dinamikát fogunk látni? Vegyük észre, hogy a két feladat között alapvető különbség van: míg a diadikus leképezés (szakaszosan) folytonos, addig a kis rágcsálók populációit leíró leképezés diszkrét, hiszen a lemmingek létszámát jelentő Xi változó csak egész értékeket vehet fel.
Először vizsgáljuk meg kis N küszöbszám esetén a lemmingpopuláció viselkedését! Az egyszerűség kedvéért tekintsünk el attól a problémától, hogy 1 lemmingből hogyan lesz 2 lemming. Ha N=13, és 3 lemminggel indítunk, akkor a következő viselkedést tapasztalhatjuk: 3®6®12®11®9®5®10®7®1®2®4®8®3. (Vegyük észre, hogy ez egy K=12 hosszúságú ciklus.) Természetesen, ha zérus lemminggel kezdünk, akkor is „ciklikus” a viselkedés, a ciklus hossza egy: 0®0. Ha a lemmingek X0 kezdeti létszámát egyenletesen sorsoljuk az {0, 1, 2, …, 12} halmazból, akkor tehát N=13 esetében 12/13 valószínűséggel olyan statisztikát kapunk, amely az {1, 2, …, 12} halmaz minden eleméhez 1/12 valószínűséget rendel, vagyis ezen belül egyenletes eloszlást mutat és a {0} elemhez zérus valószínűséget rendel. Emellett 1/13 valószínűséggel kapunk olyan statisztikát, ami a {0} elemhez 1 valószínűséget és az {1, 2, …, 12} halmaz minden eleméhez zérus valószínűséget rendel. Összefoglalva azt mondhatjuk, hogy az N=13 eset „emlékeztet” az irracionális számoknál tapasztalt viselkedésre, amikor is a diadikus leképezés a teljes intervallumon egyenletes valószínűség-eloszlást produkált.
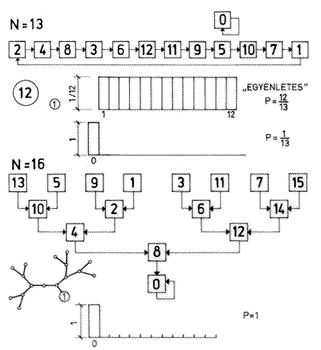
1. ábra. A lemmingpopuláció dinamikáját jellemző gráf az N=13 és N=16 esetben
Gyökeresen más a helyzet, ha az N=16 esetet vizsgáljuk, ekkor ugyanis azt tapasztaljuk, hogy függetlenül az induló létszámtól, a populáció legfeljebb 4 lépésben kipusztul, vagyis az egyelemű 0®0 ciklusba (más néven fixpontba) fut bele a trajektória legfeljebb 4 iteráció után. Néhány példa: 3®6®12®8®0; 5®10®4®8®0; 7®14®12®8®0. Az N=13 és N=16 eseteket dolgozza fel grafikusan az 1. ábra. Nagy N-ek esetén is azt tapasztaljuk, hogy az N küszöbszám kismértékű (akár eggyel történő) megváltoztatása teljesen átrendezi a dinamikát. Az 1. ábrán bemutatott, körökből álló. áttekintő gráf segítségével még viszonylag nagy N esetén is tömören jellemezhetjük a dinamika jellegét, a 2. ábrán az N=651, 652, 653, 654 eseteket tüntettük fel. (A folytonos, irracionálisokat is magában foglaló esetre leginkább azok a gráfok emlékeztetnek, ahol egyetlen, N–1 méretű ciklus alakul ki a fixpont mellett, hiszen ekkor „majdnem minden” kezdőértékre „majdnem egyenletes” eloszlást mérhetünk. Érdekes kérdés, hogy N milyen értékei mellett számíthatunk erre a viselkedésre. Jelenleg az sem ismert, hogy van-e ilyen tulajdonsággal rendelkező, tetszőlegesen nagy N szám. Vinogradov klasszikus számelméletkönyvének (Vinogradov, 1951.) egyik feladványa alapján annyit tudunk, hogy ha N=4p+1 alakú prímszám, ahol p maga is prímszám, akkor a gráf biztosan ilyen szerkezetű, de ez nem szükséges feltétel. Eddigi példáinkban 13=4·3+1, 653=4·163+1. Numerikus számítások azt mutatják, hogy az ilyen N-ek, hasonlóan a prímekhez, gyakran „ikerpárban”, egymástól 2 távolságra bukkannak fel.)
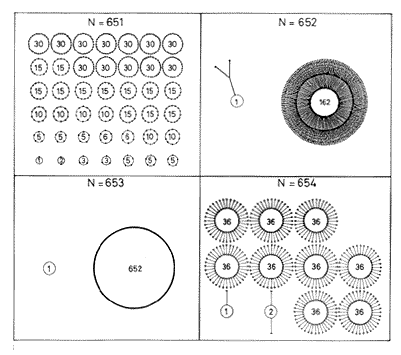
2. ábra. A lemmingpopuláció dinamikáját összegző gráf az N=651,
652, 653, 654 esetekben
Bár a lemmingpopuláció kétségkívül rendkívül komplex viselkedést mutat, első ránézésre talán nem egyértelmű, hogy ennek a komplexitásnak mi a kapcsolata a Rényi által a diadikus leképezésben felfedezett komplexitással. Az utóbbi esetében beszélhettünk a kezdeti feltételekre való érzékenységről. Bár a lemmingeknél esetenként tapasztalhatunk analóg jelenséget, általánosságban nem érvényes ez a tulajdonság: gyakran előfordul ugyanis, hogy a trajektóriák nemhogy távolodnának, de éppenséggel közelednek, például a korábban említett N=16 esetben minden trajektória befut az X=0 fixpontba. Invariáns mérték létezéséről sem beszélhetünk, bár láttuk, hogy a Vinogradov-típusú N-ek esetében látszólag „majdnem” létrejön az egyenletes eloszlás. Mi tehát az egzaktul megfogalmazott kapcsolat a diszkrét rendszer (lemmingek) és a folytonos (diadikus leképezés) között? A lemmingek leírására végtelenül sok diszkrét leképezést használunk, minden N-re más a leképezés szerkezetét jellemző gráf. Figyeljük meg azonban, hogy az összes diszkrét leképezés összes lehetséges trajektóriájához kivétel nélkül, egyértelműen hozzárendelhető a folytonos leképezés egy-egy trajektóriája, éppen a már bemutatott xi=Xi/N transzformáció segítségével. Másként úgy is fogalmazhatunk, hogy a diszkrét leképezések végtelen halmaza tartalmazza a folytonos leképezés összes véges periódusú (racionális számokon futó) trajektóriáját.
A fenti megfigyelésből az következik, hogy a folytonos esetben tapasztalt, kezdeti feltételre való érzékenységgel analóg tulajdonság a diszkrét leképezésnél az N küszöbszámra való érzékenység. Legyen például X0=5, N1=100, N2=99. Az első esetben 4 elemű, a második esetben 30 elemű ciklusba jutunk. A radikális eltérést a folytonos leképezés kezdeti feltételekre való érzékenysége világítja meg, itt ugyanis az első trajektória az x0=5/100=0,05, a második pedig az x0=5/99=0,050505 kezdőértéknek feleltethető meg.
A lemmingek példájából leszűrhetjük azt a tanulságot, hogy egy diszkrét dinamikai rendszer viselkedésére vonatkozóan a folytonos modell kevés konkrét információt szolgáltat. Felmerülhet azonban a kérdés, hogy a folytonos modell – diszkrét jelenség szakadék áthidalható-e egyáltalán. Érdekes módon a tudomány történetében elsőként a kérdés inverzével kezdtek foglalkozni: tegyük fel, hogy adott egy természeti folyamat, melyet egy folytonos modell jól közelít. A számítások során szükségképpen diszkretizálunk, tehát végeredményben egy diszkrét modellt alkalmazunk, és ekkor a folytonos jelenség – diszkrét modell ellenpont jelenik meg. A két probléma természetesen – matematikai szempontból – azonos, ha tehát ismerjük a választ az egyikre, a másikat is megoldottuk. Talán nem meglepő, hogy a folytonos jelenség – diszkrét modell probléma éppen az elektronikus számítógép megjelenése körül éleződött ki, hiszen a gép véges számábrázolása eleve diszkrétté tett minden műveletet. Annak megértéséhez, hogy milyen kaotikus jelenségeket is próbálunk számítógéppel modellezni, rövid kitérőt kell tennünk az áramlástan területére.
Lorenz modellje és egy különös attraktor
Folyadékok és gázok áramlásának leírására ma is a klasszikus Navier–Stokes-egyenleteket használják. Bár az egyenleteket már a XIX. században felírták a newtoni mechanika alapján, megoldásukról a mai napig igen keveset tudunk. Ezeknél a parciális differenciálegyenleteknél még azt sem sikerült bizonyítani, hogy adott kezdeti feltételek mellett létezik egyáltalán megoldás, nem beszélve annak egyértelműségéről. Az imént említett kérdéseket ma is hatalmas intenzitással kutatják, ugyanis nagy a tét: a tengeri áramlatok és a légköri folyamatok megértéséhez láthatóan ez az egy út vezet. Jól látta ezt E. Lorenz is, aki úgy gondolkozott: ha nem tudjuk az eredeti egyenleteket megoldani, akkor próbálkozzunk valami egyszerűbbel! (Lorenz, 1963.) Ha egy függőleges helyzetű, kétdimenziós (síkbeli) légrétegben kellően nagy hőmérséklet-különbség alakul ki a réteg alsó és felső éle között, akkor beindul a konvekció, vagyis körkörös mozgást végző örvények keletkeznek. Ez természetesen a légköri jelenségeknek csak egy nagyon szűk szelete, de Lorenz még ezt is radikálisan egyszerűsítette, ugyanis a kétdimenziós esetre vonatkozó Navier–Stokes-egyenleteket némileg heurisztikusan (vagyis intuitív alapon, matematikailag nem pontosan indokolva) egy mindössze háromváltozós, közönséges differenciálegyenlet-rendszerrel helyettesítette. Nem vállalkozunk az egyszerűsítés matematikai hátterének bemutatására, annyit jegyzünk meg csupán, hogy Lorenz egy végtelen egyenletből álló egyenletrendszert helyettesített egy három egyenletből állóval, amely azonban részét képezi az eredeti egyenletrendszernek. Lorenz bámulatos intuíciójáról tanúskodik, hogy az ily módon drasztikusan leegyszerűsített modellben sikerült megtalálni azt a „rejtett motort”, amely – legalábbis kvalitatív értelemben – felelőssé tehető az időjárás megjósolhatatlanságáért. (Lorenz érdemeit nem csökkenti az a tény, hogy egyszerűsített modellje a paraméterek egy olyan tartományában produkálja a megjósolhatatlan viselkedést, amely a légkörben mérhető adatoktól távolabb esik.)
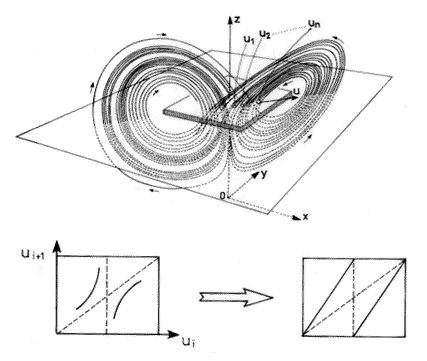
3. ábra. A Lorenz-attraktor és annak Poincaré-metszete
Differenciálegyenlet-rendszerek megoldásgörbéit célszerű az egyenlet változói által kifeszített fázistérben vizsgálni. Ez a Lorenz-egyenletek esetében egy 3 dimenziós tér. A századforduló kimagasló matematikai egyénisége, Poincaré vette észre, hogy a trajektóriáról rengeteget elárul, ha a fázistérbe helyezett síkkal való metszéspontjait ábrázoljuk. Nagy előnye a Poincaré-metszetnek, hogy csökkenti a vizsgálandó objektum dimenzióját. Egy periodikus pálya Poincaré-metszete például néhány pont, hiszen a trajektória önmagába tér vissza. A teljes, háromdimenziós térben véletlenszerűen bolyongó trajektória Poincaré-metszete síkbeli tartomány. Lorenz számításai azt mutatták, hogy az általa vizsgált egyenletek trajektóriái rendkívül érzékenyek a kezdeti feltételekre, de egy különös alakú objektum vonzza őket magához a fázistérben. Az objektum belsejében ergodikus jellegű viselkedést észlelt, vagyis tapasztalta az invariáns mérték létezését. Az ilyen objektumokat nevezzük különös attraktoroknak, a „különös” jelző arra utal, hogy dimenziójuk általában nem egész szám (Szépfalusy–Tél, 1982.). Lorenz a különös attraktort „közel” kétdimenziósnak látta, ebből adódóan a Poincaré-metszet közel egydimenziósnak, vagyis vonal jellegűnek adódott, ezt illusztrálja a 3. ábra. Ezen a vonalon bevezetve az u koordinátát, a trajektória egy ui+1=F(ui) rekurzióval adható meg, hiszen az x tengely és a trajektória metszéspontjai időben sorba rendezhetőek. Az F függvénykapcsolatot maga a differenciálegyenlet és a Poincaré-metszet elhelyezkedése egyértelműen meghatározza. A Lorenz-egyenletek esetében, alkalmasan megválasztott Poincaré-metszet esetén, az F függvény igen hasonlít a diadikus leképezéshez:
ui+1 = F(xi) = 2 ui mod 1.
Ezután természetesen nem lepnek meg bennünket Lorenz megfigyelései, meglephet viszont az a tény, hogy a diadikus leképezés nemcsak matematikai kuriózumként bukkan fel Rényi cikkeiben és nemcsak a lemmingpopulációk kvalitatív leírására használható, hanem a légköri folyamatok egy durván egyszerűsített matematikai modelljében is elbújik. Nem a diadikus leképezés jelentőségét szerettük volna túlértékelni, csupán arra mutattunk rá, hogy folytonos fizikai jelenségek leírására gyakran alkalmasak a kaotikus leképezések. Ezután természetesen vetődik fel a probléma: ha egy kaotikus leképezés diszkretizáltjából nehezen vagy alig lehet következtetni a folytonos rendszer működésére, miként lehetséges a folytonos, kaotikus leképezésekkel jellemezhető fizikai rendszerek vizsgálata számítógépek segítségével. Mint már említettük, a probléma a „levegőben lógott” az elektronikus számítógépek megjelenése pillanatában és maga Neumann János is nagy figyelmet szentelt neki. Az ő meghívására érkezett a II. világháború után Princetonba az a fiatal matematikus, akinek a nevéhez alapvető eredmények fűződnek ezen a területen.
Ulam sémája
Stanislaw Ulam különleges tehetség volt. Egyik fő feladatául a Teller Ede által tervezett hidrogénbombához kapcsolódó számításokat jelölték meg. Ulam hamarosan kimutatta, hogy Teller eredeti ötlete nem működik, és matematikus létére aktívan részt vett egy működő séma kidolgozásában. Az ergodikus leképezések trajektóriáinak pontos kiszámítása elvben lehetetlen feladat, Ulam azonban rájött, hogy a leképezést statisztikus értelemben jellemző invariáns valószínűségi mérték viszont jól közelíthető alkalmas módszerrel (Ulam, 1960.). Az invariáns sűrűségfüggvény előállítása az egységintervallumon egy (végtelen dimenziós) függvényegyenletre vezet. Ulam azt javasolta, hogy ezt diszkretizáljuk oly módon, hogy az egységintervallumon felvett osztáspontok közötti függvényt átlagoljuk. Az átlagolt feladat egy véges dimenziós egyenletrendszert eredményez, amely elvben megoldható. Ulam kivételes intuíciója nem csalt: ellentétben az egyes trajektóriák egyedi kiszámításánál tapasztaltakkal, a megoldás jól konvergál a pontos sűrűségfüggvényhez, ha a rácsot sűrítjük. Szépséghiba Ulam sémájában, hogy maga az eredeti leképezés is csak az osztópontokban ismert, ráadásul ott is csak a gépi számábrázolás pontosságával, így a megoldandó egyenletrendszer együtthatói pontatlanok, tehát a végeredmény sem lehet teljesen pontos. Érdekes módon ennek a szépséghibának a kiküszöbölése elvezet az Ulam-séma mélyebb megértéséhez. Bizonyítható ugyanis (Domokos és Szász, 2002.), hogy a séma ekvivalens a diszkretizált leképezés egy speciális, véletlenszerű megzavarásával. A korábban részletesen vizsgált, diszkretizált diadikus leképezés esetén az Ulam-sémának megfeleltethető, véletlennel megzavart leképezés igen egyszerű alakot ölt:
Xi+1 = 2 Xi mod N + zi,
ahol a zi valószínűségi változó 50% valószínűséggel 0, és 50% valószínűséggel 1 értéket vesz fel, ezt szemlélteti a 4. ábra. Általánosságban az Ulam-sémának megfelelő véletlen zavarást reprezentáló zi diszkrét valószínűségi változó mindig egyenletes eloszlású, és értékkészletének (esetünkben ez a {0, 1} halmaz) elemszáma megegyezik a leképezés D deriváltjával (esetünkben D=2). A megzavart diszkrét rendszer trajektóriáiból nyert statisztika konvergál az eredeti, folytonos leképezés invariáns sűrűségfüggvényéhez. A diszkretizálás során az eredetileg végtelenül sűrű információt hordozó trajektóriák véges információtartalmúvá egyszerűsödnek. A véletlen viszont a legnagyobb lehetséges információsűrűségű folyamat, tehát a véletlen zavarás által a diszkretizálás során elvesztett információt csempésszük vissza a rendszerbe. Természetesen a zavarás mértéke nem közömbös, hiszen túl nagy zavarás esetén már nem az eredeti rendszert, hanem a zavarás statisztikus jellemzőit látnánk viszont a statisztikában. Megmutatható, hogy Ulam sémája éppen egy minimális véletlen zavarással egyenértékű. Érdekes kérdés, hogy miként állítható elő digitális számítógép segítségével a megzavaráshoz használt véletlen mennyiség (a diadikus leképezés esetében a zi valószínűségi változó). Igazi véletlen – éppen az elmondottak miatt – digitális gép és véges algoritmus segítségével nem produkálható, ezért itt pszeudovéletlen (vagy álvéletlen) mennyiségeket használunk (Lovász, 2000.).
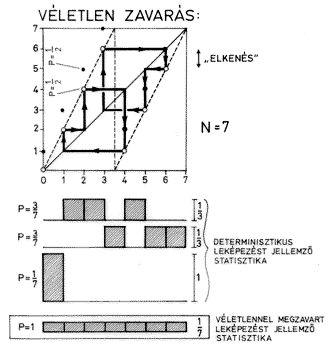
4. ábra. Ulam sémája a diadikus leképezés esetében
Láthatjuk tehát, hogy Ulam sémája, illetve az ezzel ekvivalens eljárás a folytonos, kaotikus rendszer és annak diszkretizáltja közötti szakadékot az utóbbi véletlen zavarásával hidalja át. Ez a gondolat természetesen a másik irányban is működik: ha a lemmingek szaporodási szokásai nem követik pontosan a diadikus modell szerinti törvényt, hanem ahhoz képest véletlen fluktuációk mutatkoznak, akkor azt várhatjuk, hogy a populáció egészét statisztikai értelemben jól leírja a folytonos diadikus leképezés (vagyis minden lemminglétszám közel azonos valószínűséggel fordul elő). Furcsa módon tehát a diszkrét dinamika „pontatlansága” garantálja, hogy a folytonos modellből statisztikai értelemben pontos következtetéseket vonhassunk le. A dolgozatban bemutatott diadikus leképezés talán a legegyszerűbb példa ilyen matematikai modellre, azonban alkalmas arra, hogy a kaotikus folyamatok jellegzetességeit szemléltessük.
Összefoglalás
Nem tudhatjuk, hogy miért utasították el a pitagoreusok az irracionális szám fogalmát. Tény azonban, hogy ez a fogalom kulcsszerepet játszik egyes természeti folyamatok leírásában, és éppen emiatt be kell látnunk, hogy a laplace-i világkép nemcsak a kvantummechanikában, hanem a makrovilágban is csődöt mond, ugyanis ezen kaotikus folyamatok számunkra a klasszikus, laplace-i értelemben megismerhetetlenek. (Statisztikus értelemben természetesen a folyamatok pontosan leírhatóak, de ez a megismerésnek más szintje.) Arra a következtetésre jutottunk, hogy kaotikus folyamatok modellezésekor az irracionális szám és a véletlen komplementer fogalmak abban az értelemben, hogy modellünk megalkotásakor választanunk kell a gödeli ismeretelméleti korlátokat magukban rejtő irracionális számok vagy a laplace-i kauzalitást tagadó véletlen között. Az előbbi esetben a folytonos modellt választjuk, melynek működését csak irracionális számok pontos ismeretében tudnánk leírni. A másik alternatíva a diszkrét modell alkalmazása, mely önmagában elégtelen ugyan, de véletlen zavarással már – statisztikus értelemben – jól közelíti a folytonos rendszert.
Nem kerülhetjük ki tehát a tudományos megismerés elvi korlátait (melyeket a matematika és a fizika saját maga fedezett fel és fogalmazott meg), és ez természetes következménye annak, hogy a kaotikus dinamikai rendszerek, bár determinisztikusak, mégis megjósolhatatlanok és kvantitatív értelemben megismerhetetlenek. Ellentétben a kvantummechanikával, a kaotikus dinamikai rendszerek mindennapi életünkben jól érzékelhető folyamatokat modelleznek: a Naprendszer bolygóinak mozgása, szerszámgépek, járművek gerjesztett rezgései, kémiai reakciók, ökológiai folyamatok, a légköri és tengeri áramlások, elektromos áramkörök, a kettős inga vagy a gerjesztett matematikai inga, a DNS-molekulák térbeli alakja, a leveles tészta készítése, mind-mind példa kaotikus dinamikai rendszerrel modellezhető jelenségekre, folyamatokra. Több mint kétezer évvel korábban a pitagoreusok képtelenek voltak az irracionális számot beilleszteni világképükbe. Vajon a XXI. században képesek vagyunk-e erre?
Epilógus: lemmingek a távolból
A fentiek alapján talán az a kép alakult ki az olvasóban, hogy a kaotikus dinamikai rendszerek vizsgálata óhatatlanul bizonytalanságba, pontatlan leírásba torkollik, azonban ez nincs feltétlenül így, sőt az ellenkezőjére mutatunk most példát. Tételezzük fel, hogy két lemmingpopulációt figyelünk meg (távolról), és mindkét populáció pontosan, véletlen fluktuációk nélkül a diadikus leképezés szabályai szerint szaporodik. Célunk a (részleges vagy teljes) pusztuláshoz rendelt N1 és N2 küszöbszámok meghatározása, eszközünk a lemmingek létszámának ismételt, de (az eszközök fogyatékosságából, illetve a távolságból adódóan) kissé pontatlan megfigyelése. Tudjuk, hogy méréseink hibája legfeljebb 2 lemming, tehát ha a mérés eredménye x, akkor a valódi létszám az [x–2, x+2] intervallumban van. Az alábbi két adatsor áll rendelkezésünkre:
1. adatsor:
4®7®11®22®20®7®20®8®13®30®26®25®23®14®28®23®15®4®11®21®13®20®14®1®1®3®8®17®5®6®10®23®19®11®17®7®15.
2. adatsor:
4®6®14®22®18®0®0®0®0®0®0®0®0®0.
A lemmingek létszámában csökkenés csak a küszöbszám meghaladásakor állhat be. Láthatjuk, hogy az első adatsor esetében a küszöbszám legalább 29, hiszen egy alkalommal mértünk 30-as létszámot, a tényleges létszám ekkor legalább 28 volt és a populáció nem pusztult ki, tehát N1>28. Azt is megállapíthatjuk viszont, hogy a 14-es mért létszámadat után csökkenés következett be, tehát N1<(2·(14+2))=32. Vegyük észre, hogy a pontatlan mérések mögött csak periodikus viselkedés húzódhat meg (ellenkező esetben a populáció kihalt volna). A periódus K hosszát megtudhatjuk, ha megvizsgáljuk, hogy egymástól K távolságra lévő létszámadatok különbségének mennyi a maximuma: ha ez a szám 4 vagy kevesebb, akkor lehet, hogy K a periódus hossza, és az eltérések csak a mérési hibából adódnak. Egy táblázat vagy egy rövid BASIC program segítségével meggyőződhetünk róla, hogy ez a maximális különbség egyedül K=28 esetén lesz 10 alatt, ekkor éppen 4, tehát a ciklus hossza éppen 28. Vegyük észre, hogy 29 éppen Vinogradov-típusú szám, vagyis olyan prím, mely egy másik prím négyszeresénél eggyel több. Ebből az következik, hogy N1=29 esetén a fixpont mellett éppen egy 28 hosszúságú ciklus alakul ki (és más, a környékén lévő N-re ez nem teljesül). A fenti okoskodás alapján biztosan állíthatjuk, hogy N1=29, és visszaállíthatjuk a mért, pontatlan adatokból a pontos, valódi adatsort:
3®6®12®24®19®9®18®7®14®28®27®25®21®13®26®23®17®5®10®20®11®22®15®1®2®4®8®16®3®6®12®24®19®9®18®7®14.
A második adatsor esetén könnyebb a dolgunk, hiszen a populáció 5 lépésben kihal. Az ötödik lépés alapján megállapíthatjuk, hogy 31<N2<41. Ebben az intervallumban megvizsgálva a leképezéshez tartozó gráfokat kiderül, hogy csak N2=32 esetén van olyan 5 lépéses trajektória, amely a zérus fixpontba vezet, tehát N2=32, és a pontos adatsor rekonstruálható:
3®6®12®24®16®0®0®0®0®0®0®0®0®0
A példa azt mutatja, hogy a káosz nemcsak bizonytalanság, hanem információ forrása is lehet. (Folytonos rendszerekben a trajektória mérése jelenthet új információt (Szépfalusy–Tél, 1980.)) Példánkban kihasználtuk, hogy a diszkrét rendszer dinamikája érzékeny az N küszöbszámra, és közeli N-ek esetén radikálisan eltérő viselkedést mutat. Ezeket a radikálisan eltérő dinamikákat már pontatlan adatok alapján is képesek voltunk pontosan rekonstruálni. Példánk szempontjából teljesen mindegy, hogy az adatok bizonytalanságának forrása gyakorlati (távolság, műszerpontatlanság) vagy elvi jellegű.
Köszönetnyilvánítás
A szerző Scheuring Istvánnak, Szász Domokosnak, Tél Tamásnak
és Tóth Rékának mond köszönetet értékes javaslataikért és megjegyzéseikért.
A munka az OTKA 031744 témája és a Bolyai Ösztöndíj támogatásával készült.
Irodalom
Brehm, A.: Az állatok világa. ÁKV–Maecenas Kiadó, Budapest, 1990.
Domokos G., Szász D.: Ulam’s scheme revisited: digital modeling of chaotic attractors via micro-perturbations. Discrete and Continuous Dynamical Systems, Series A, 2002. https://www.ma.utexas.edu/mp_arc-bin/mpa?yn=02–170
Lorenz, E. N.: J. Atmospheric Science, Vol. 20. pp. 130–141., 1963.
Lovász L.: Véletlen és álvéletlen. Természet Világa, Vol. 131. II. (informatikai) különszám, pp. 5–8., 2000.
Szépfalusy P., Tél T.: A káosz. Akadémiai Kiadó, Budapest, 1982.
Ulam, S.: Modern problems in mathematics. Interscience Publishers, 1960.
Vinogradov, I. M.: A számelmélet alapjai. Tankönyvkiadó, Budapest, 1951.
| Természet Világa, | 133. évfolyam, 10. szám, 2002. október
https://www.chemonet.hu/TermVil/ https://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez