
t » (2R)2 - 2(2R/3)2 = 28/9 R2
MATEMATIKA
Petz Dénes
Mérték és dimenzió
A terület az egyik legrégibb matematikai fogalom. A háromszög, trapéz, és kör területképletét az iskolában tanítják. Területszámítással már az ókori egyiptomiak és görögök is foglalkoztak. A téglalappal összevetve bonyolultabb kör területének kiszámításakor a ma p-nek jelölt számot az egyiptomiak még 3,11-nak, a görögök már jobb közelítéssel 22/7-nek vették.
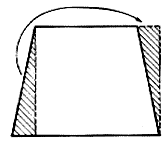
Jó néhány síkbeli alakzat területét kiszámíthatjuk úgy, hogy ismert területû darabokra vágjuk ôket. A terület daraboláskor összeadódik, ez egy lényeges tulajdonsága, amivel már az egyiptomiak is tisztában voltak. Területszámítási módszereikrôl az úgynevezett "Rhind" papíruszból alkothatunk fogalmat. Az i. e. 1650-ben készült papírusztekercs másolója azt írja, hogy az eredeti a középbirodalom idejébôl, tehát körülbelül az i. e. 2000-1800 idôszakból származik. A papírusz 20 térfogat- és területszámítással foglalkozó feladatot és azok megoldásait tartalmazza. Megtudhatjuk, hogy a 4 és 6 egységnyi alapokkal rendelkezô és 20 egység magas szimmetrikus trapéz területe 100, mivel 5 és 20 egység oldalhosszú téglalappá darabolható át.
 |
 t » (2R)2 - 2(2R/3)2 = 28/9 R2 |
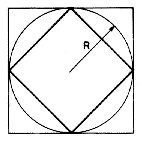
| 1. ábra. Szimmetrikus trapéz területének kiszámítása egyiptomi módra átdarabolással: a trapézt vele egyenlô területû téglalappá darabolhatjuk át | 2. ábra. A kör területének közelítése egyiptomi módra nyolcszög segítségével: az R sugarú kör területét megközelítôleg úgy kaphatjuk meg, hogy a 2R oldalhosszú négyzet területébôl elvesszük két darab 2R/3 oldalhosszú négyzet területét |
A papíruszra írt példából következtethetünk arra, hogy a kör területének kiszámításakor milyen módszert használhattak az egyiptomiak. Ha a négyzet oldalait három egyenlô részre osztjuk, és az osztópontok ábra szerinti összekötésével kapott négy kis háromszöget levágjuk a négyzetbôl, akkor egy olyan nyolcszöget kapunk, amelynek területe közelítôleg a négyzetbe írt kör területe. A nyolcszög területe egy átmérô oldalhosszú négyzet területének és két egyharmad átmérô oldalhosszú kisebb négyzet területének a különbsége. Az egyiptomiak még nem használtak a mai értelemben vett matematikai képleteket, a nyolcszög segítségével kapott közelítésüket ma így írnánk: t = 28/9 R2. A kör területszámításának ez a módszere a p szám 3,111 értékének felel meg.
A babiloni matematika általában véve sokkal fejlettebb volt, mint az egyiptomi, például a Ö2-t meglepôen pontosan ismerték 60-as számrendszerükben:
1 + 24/60 + 51/602 + 10/603 = 1,414213
 t » {(2R)2 + [(2R)2 - 2R2]}/2 = 3R2 |
| 3. ábra. A kör kerületének közelítése babilóni módra, a beleírt és a köré írt négyzet segítségével: az R sugarú kör köré írt 2R oldalú négyzet és a körbe írt 2R átlójú négyzet területének átlagát vesszük |
Ennek ellenére a kör területszámításában alulmaradtak az egyiptomiakkal szemben. A babiloniaiak a kör területét úgy közelítették, hogy a beleírt és a köré írt négyzetek területének átlagát vették. Bárki utánaszámolhat, hogy ez a közelítés csak a p szám 3 értékének felel meg.
A síkbeli alakzatok területének a darabolhatóság mellett másik alapvetô tulajdonsága az, hogy egy alakzatot elmozgatva a területe nem változik meg. A terület nagytestvére a térfogat. Térfogata térbeli alakzatoknak van, hogy pontosan melyeknek, az nehéz kérdés, és most nem érintjük. Mindenesetre, ha két térbeli alakzat térfogatáról beszélhetünk, és nem metszenek egymásba, akkor egyesítésüknek is van térfogata, és az a két térfogat összege. A térfogat is érzéketlen a mozgatásokra, azaz eltolás és elforgatás során változatlan marad. A terület és a térfogat egyaránt halmazfüggvények, a sík, illetve a tér bizonyos részhalmazaihoz rendelnek számokat. Rendelkeznek az additivitásnak nevezett t(A U B) = t(A) + t(B) tulajdonsággal, ha A és B nem metszenek egymásba. Az additív halmazfüggvényeket a matematikában mértéknek nevezik. A területmérték és a térfogatmérték a legtermészetesebb példák.
A területmértéket három tulajdonságával lehet axiomatikusan meghatározni. Ezek jórészt említésre kerültek, de a teljesség kedvéért még egyszer kifejtjük ôket. Elôször az additivitás: ha egy alakzatot egymásba nem nyúló részekre bontunk, akkor azok területének összege a felbontott alakzat területe. Másodszor az invariancia: síkbeli mozgatás a területet nem változtatja meg. Harmadszor a normálás: az a négyzet, amelyet területegységnek választunk, 1 területû. (Értelemszerû kis változtatással a térfogatmérték is hasonlóan határozható meg.)
A sík, illetve a tér részhalmazainak mértékéhez hasonlóan egy gömbfelület részhalmazait is nézhetjük. Az egyszerûség kedvéért gondoljunk egy gömbsüvegre vagy egy gömbháromszögre. Egy olyan tengely körüli forgatás, amely átmegy a gömb középpontján, a gömbfelület pontjait a felületen megtartja, és például egy gömbsüveget egy másik gömbsüvegbe visz. A gömbfelület részhalmazainak területmértéke olyan mennyiség kell, hogy legyen, amely az ilyen forgatásokra invariáns. Annak ellenére, hogy csak kevés gömbfelületi tartomány területét tudnánk konkrétan kiszámítani, világosan látjuk, hogy a gömbfelületen is létezik területszámítás, éppen úgy, ahogy a síkon.
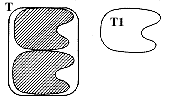
A 20. század elejére sok hasonló példa gyûlt össze, pontosabban példák olyan mértékekre, amelyek invariánsak voltak bizonyos transzformációkra. Ezek közül fent a síkbeli területmértéket, a térbeli területmértéket, a gömbfelületi területet említettük, de további példa lehetne a Bolyai-síkon vett terület és sokfajta bonyolult mérték. A példák láttán a matematikában nem alaptalanul gondoltak arra, hogy valamilyen mélyebb összefüggés áll a háttérben. Ennek bizonyítása sokáig mégse sikerült. Haar Alfréd magyar matematikus volt az elsô, aki az invariáns mértéket teljes általánosságban megkonstruálta és egyértelmûségét is bebizonyította. Haar Alfréd gondolatát síkbeli tartományokon fogom érzékeltetni. Válasszunk egy korlátos síkbeli T1 tartományt, ami a területegység szerepét fogja játszani. Mivel általános meggondolásra törekszünk, nem gondolhatjuk, hogy T1 egy négyzet, hanem egy szabálytalan "foltra" kell gondolnunk, amely az ábrán talán a festôk palettájára emlékeztet. Feladatunk az, hogy T1 segítségével tetszôleges T tartományt "megmérjünk". A mértéknek mozgatásra invariánsnak kell lenni, tehát T1-et akárhova eltolva szintén 1 mértékû tartományt kapunk. Ha T-be beletolhatjuk T1 egy példányát, akkor biztos, hogy T mértéke legalább 1, ha T1 két példányát pakolhatjuk be T-be úgy, hogy azok nem lógnak egymásba, akkor T mértéke legalább 2 és így tovább. Gondolatban próbáljuk ki az összes lehetôséget, és nézzük meg, hogy T1-nek legfeljebb hány elmozgatott példánya fér bele T-be. Legyen ez az egész szám n1. Így n1 valamiféle alsó közelítése T mértékének, de természetesen az is lehetséges, hogy n1 = 0, még akkor is, ha T sokkal nagyobb területû, mint maga a területegység, T1.
 |
 |
| 4. ábra. Egy tartomány területének közelítése a T1 területegység segítségével: T1 egy folt alakú tartomány, amelynek két példánya fér bele a lekerekített sarkú téglalapra emlékeztetô T-be. Ezért T területmértéke körülbelül 2 | 5. ábra. A terület jobb közelítése a kisebb U tartományt használva: U egy trapéz alakú tartomány, területe körülbelül 1/2. T-be U-nak 7 példányát tehetjük bele, így T területe megközelítôleg 7/2. Az igazság 2 és 7/2 között van. Nagyon jó közelítést csak akkor fogunk kapni, ha U igen kicsiny |
Ahhoz, hogy jobb közelítést kapjunk, "váltsuk fel" T1-et, és vegyünk egy kisebbU-t. Természetesen nem vehetünk egy éppen fele akkora mértékût, mivel nem tudjuk, hogy a szabálytalan T1-et hogyan lehetne pontosan megfelezni. Gondolatban megint megnézzük, hogy U hány darab elmozgatott példánya rakható be T-be optimálisan. Legyen ez a szám nu. Sajnos nu már nem közelíti T mértékét, hiszen ha U nagyon piciny, akkor az nu egész szám nagyon nagy is lehet. Kellene tudnunk, hogy mekkora U mértéke. Ezért nézzük meg, szokásunk szerint természetesen gondolatban, hogy U eltoltjaiból hány darab pakolható be T1-be úgy, hogy egymásba ne lógjanak. Ez a szám legyen mu. Mivel T1 egységnyi mértékû, U mértéke körülbelül 1/mu kell, hogy legyen. Ekkor viszont T mértéke megközelítôleg nu-szor 1/mu, azaz nu/mu. Ha U-t egyre kisebbnek választjuk, akkor az nu/mu közelítés egyre jobb lesz, és határértékben megadja a pontos mértéket. Ez Haar Alfréd egyszerû, de zseniális gondolata! Igen-igen általános, csak az kellett hozzá, hogy az U tartományokat akárhova elmozgathassuk és akármilyen picire választhassuk.
A transzformációkkal szemben invariáns mérték Haar Alfréd kortársát, Neumann Jánost is foglalkoztatta. Neumann és Haar levelezésben álltak, egymást kölcsönösen tájékoztatták új tudományos eredményeikrôl. Abban az idôben, amikor Haar a Szegedi Egyetem professzoraként felfedezte az általános invariáns mértékét, Neumann Németországban dolgozott. Neumann Jánost sokan a század egyik legnagyobb matematikusának tartják, azon túlmenôen is, hogy úttörô szerepe volt a számítógépek fejlesztésében is. Neumann János fiatalkora egybeesett a fizika forradalmával, az úgynevezett kvantumfizika kialakulásával. A fizika nemcsak Newton idejében volt elválaszthatatlan a matematikától. Akkor a mechanika igényelte és inspirálta a differenciál- és integrálszámítás létrejöttét. A kvantumelmélet a század elsô harmadában a lineáris operátorok mélyreható analízisét kívánta. Neumann János és több kiváló matematikus fáradozott azon, hogy létrehozza az újfajta matematikát. Eközben fedezte fel Neumann János azt a folytonos geometriát, amiben a dimenzió nem csupán egész számértéket vehet fel.
A dimenzió - sajnos - sokkal kevésbé szemléletes fogalom, mint a terület. Ez a megfoghatatlansága teszi alkalmassá arra, hogy fantasztikus regényekben a hôsök esetleg a világûr fekete lyukain keresztül távozzanak a negyedik vagy akár magasabb dimenziókba. A fizikai tér háromdimenziós, ha az idôt is hozzávesszük, akkor esetleg négy. Mi értelme van akkor magasabb vagy tört dimenzióknak? A sokdimenziós teret megérthetjük két tömegpont példáján. Ha a két tömegpont pillanatnyi állapotát akarjuk megadni, akkor 3-3 helykoordinátára van szükségünk, ami már önmagában 6 adat. Kell még 3-3 sebességkomponens is, ami összesen 12 adat. Az egy idôponthoz tartozó 12 szám egy 12 dimenziós matematikai tér egy pontjának tekinthetô.
Felületesen azt gondolnánk, hogy a dimenzió és a területmérték közötti alapvetô különbség éppen az, hogy az elôbbi csak egész számértékeket vehet fel, az utóbbi pedig akármilyen pozitív számot. Neumann János azt fedezte fel, hogy ez nem így van, sôt a rokonság a két fogalom között nem is olyan távoli, ha az absztrakció elég magas szintjére vagyunk hajlandók feljutni.
A lineáris dimenzió mindig egy vektortérhez kapcsolódik. Egy sík vektorai kétdimenziós teret képeznek, mert van két vektor, amelyek kifeszítik a síkot, abban az értelemben, hogy a sík bármely vektora a két kiválasztott vektor számszorosai összege. Tudjuk, hogy bármely két nem párhuzamos vektor jó erre a célra, de egy vektor viszont nem elegendô. Hasonlóan, vagyis inkább egyszerûen látható módon, egy egyenes vektorai egydimenziós teret alkotnak, mert egy egyenes minden vektora bármelyik egyenesbe esô vektor számszorosa. Általában egy vektortér n-demenziós, ha van n vektora, amelyekbôl vektora számmal való szorzással és összeadással megkapható, de n-1 vektor ehhez sohasem elegendô. Azt is szokták ekkor mondani, hogy a tér n vektorral kifeszíthetô, de n-1 vektorral már nem. Két egydimenziós vektortér egy kétdimenziós teret feszít ki, kivéve azt az esetet, amikor egybeesnek. Egy kétdimenziós vektortér és egy egydimenziós vektortér háromdimenziós teret feszít ki, kivéve azt az esetet, ha az egydimenziós benne van a kétdimenziósban. Ha egy vektortér két altere nem nyúlik egymásba, akkor az általuk kifeszített altér dimenziója a két altér dimenziójának összege. Ez emlékeztethet bennünket a területnek arra a tulajdonságára, hogy két egymásba nem nyúló alakzat egyesítésének területe a két terület összege. A terület az egybevágósági transzformációkkal szemben invariáns. Van esetleg olyan mozgáscsoport, ami egy vektortér dimenzióját nem változtathatja meg, vagyis amire nézve invariáns a dimenzió? Ha az egész vektorteret úgy transzformáljuk önmagába, hogy az a transzformáció a vektortér lényeges tulajdonságait megtartja, azaz a vektorok hosszát és egymással bezárt szögét nem változtatja meg, akkor egy alteret ugyanolyan dimenziójú altérbe fog vinni, akárhogyan is értjük a dimenzió fogalmát. A vektortér-struktúrát megtartó transzformációkat, amelyeket az elôzôekben említettünk, lineáris izometriáknak nevezik. Talán meglepô, hogy arra a következtetésre jutottunk, hogy némi hasonlóság van a területmérték és a vektortér dimenziója között. Mindkét számértékû mennyiség változatlan marad bizonyos transzformációk alkalmazásánál. A terület esetében az ilyen transzformáció az eltolás és elforgatás, a dimenzió esetében pedig a lineáris izometria alkalmazása. A két példában az additivitás egyaránt jelen van. A terület additivitása könnyen megérthetô, a dimenzió additivitása egy kicsit összetettebb.
Neumann János ezek után úgy jutott el a folytonos geometriához, hogy vett egy végtelen dimenziós vektorteret, és abban kijelölt lineáris izometriáknak egy csoportját, továbbá lineáris alterek egy osztályát. Ezt úgy kellett megtenni, hogy egy kijelölt alteret egy kijelölt lineáris izometria kijelölt altérbe vigyen, hasonlatosan ahhoz, ahogy egy síkbeli ponthalmazt, aminek a területérôl beszélni lehet, egy síkbeli mozgatás egy területtel rendelkezô síkbeli ponthalmazba visz. Természetesen itt nem tudunk részletekbe bocsátkozni arról, hogy ez a "kijelölés" hogyan történik. Neumann János észrevette, hogy Haar Alfréd mértékelméleti gondolata ebben a helyzetben is mûködni tud, ha a tartományokat a lineáris alterekkel és a mozgáscsoportot a lineáris izmetriákkal helyettesítjük. Választott ezért egy T1 alteret, amire azt mondta, hogy annak a dimenziója lesz az egységdimenzió, vagyis ezt a T1-et használta dimenzióegységül. Egy olyan altér, amit T1 két egymásba nem nyúló transzformáltja feszít ki, kétdimenziós lesz. Ha viszont találunk olyan T alteret, amelynek három egymásba nem nyúló transzformáltja feszíti ki T1-et, akkor nincs más választásunk, minthogy ezt a T alteret 1/3 dimenziósnak tekintsük. Lényegében ez Neumann János folytonos geometriája, amit a fizika kvantumelmélete inspirált. Két egymásba nem nyúló 1/3 dimenziós altér kifeszít egy 2/3 dimenziósat, és ha a kijelölés valóban elég körültekintô volt, akkor minden 0 és 1 közötti számhoz tartozik egy ilyen dimenziójú altér.
Talán a tudománytörténet fintora, hogy a kvantumelmélet, ami éppen azon alapul, hogy az energia nem vehet akármilyen kicsi értéket, hanem csak egy igen pici (hatáskvantum) többszöröseit, indította el Neumann Jánost abba az irányba, hogy felfedezzen egy olyan geometriát, amiben a dimenzió akármilyen kicsi értéket is felvehet, nem csupán egy érték többszöröseit.
| Természet Világa, | 128. évf. 3. sz. 1997. március. 118-120. o. |
| https://www.kfki.hu/chemonet/TermVil/ | |
| https://www.ch.bme.hu/chemonet/TermVil/ |