a bromát malonsav Ce(IV) rendszerben
NÉZÔPONT
"Jósolni nagyon nehéz,
különösen, ha a jövôrôl van szó."
(Niels Bohr)
BECK MIHÁLY
Mit hoz a jövô?
Jóslás és
tudományos elôrelátás
Akár a mindennapi életben, akár a tudomány vilagában aligha van kívánatosabb dolog, mint tudni azt, hogy milyen eseményekre kerül sor a jövôben. Ôsidôk óta ismeretesek a legkülönbözôbb jóslási módok, melyektôl az egyes emberek, illetve nemzetek vagy akár az egész emberiség jövôjére vonatkozóan reméltek felvilágosítást szerezni. A természettudományok különbözô ágaiban pedig nagy szerepet játszanak azok a törekvések, amelyek a különbözô természeti, illetve kísérletes folyamatok idôbeli lejátszódásának, bekövetkezésének törvényszerûségei felderítésére irányulnak. Célszerû lesz elôször néhány természettudományi példát megvizsgálni, majd a tudományos, a társadalmi és a politikai futurológia kérdésével foglalkozni, mielôtt a tulajdonképpeni jóslási módok lehetôségeit elemeznénk.
Tudományos elôrejelzés a csillagászatban
A csillagászat tudománya évezredek gondos megfigyelései során fejlôdött ki. Elôször csak a szabad szemmel megfigyelhetô égitestek mozgását követték nyomon. A távcsô feltedezésével lényegesen megnövekedett az ismertté vált égitestek száma. Kepler és Newton munkássága nyomán fejlôdött ki az égi mechanika tudománya, lehetôvé téve az egyes bolygók, illetve holdjaik pályájának nagy pontosságú, bár a probléma természetébôl adódóan csak közelítô leírását. Arra is mód nyílt, hogy a számított és az észlelt pályák külünönbségébôl addig nem ismert égitestek létezésére következtessenek. Le Verrier az 1781-ben felfedezett Uránusz bolygó pályáját vizsgálta, és 1845-ben azt találta, hogy nem elegendô a Szaturnusz és a Jupiter perturbációs hatását figyelembe venni, hanem kell lennie egy, azok pályáján túl levô bolygónak is. Kiszámította e bolygó pályáját, és 1846. szeptember 24-én Gallei fel is fedezte azt a Le Verrier által megjelölt helyen.
Közhellyé vált a csillagászati pontosság kifejezés. Tetszés szerinti véges idôpontra elôre meg tudják adni az égitestek helyét. Arra azonban nincsen mód, hogy elôre jelezzék pl. egy meteor vagy addig ismeretlen üstökös feltûnését!
A kémiai reakciók idôbeli lefolyása
A kémiai reakciók kinetikai vizsgálatával, azaz az egyes anyagfajták koncentrációi idôbeli változásának követésével és e változások törvényszerûségeinek feltárásával csak a múlt század közepe óta foglalkoznak. Természetesen már sokkal régebben tudták, hogy a különbözô reakciók lényegesen különbözô sebességgel játszódnak le, de csak ekkorra értek meg a kísérleti és elméleti feltételek a tudományos igényû reakciókinetikai vizsgálatokra.
Általánosságban megfogalmazva, a reakciókinetika elsôdleges célja annak megállapítása, hogy adott kezdeti feltételek esetében milyen matematikai egyenletekkel írható le a különbözô anyagfajták mennyiségének, illetve koncentrációjának változása az idôben, hogyan változik a reakció, illetve az anyagfajták koncentráció-változásának sebessége a különbözô komponensek koncentrációjának, a közegnek (oldószer), a hômérsékletnek, esetleg a különbözô erôterek (fény, elektromos és mágneses erôtér stb.) intenzitásának a függvényében. Noha számos reakciót meglehetôsen alaposan ismerünk, aligha mondható el, hogy akár csak egy olyan reakció is van, amit reakciókinetikai szempontból teljesen felderítettnek mondhatnánk, és többé-kevésbé egyértelmûen körvonalazhatók a reakciókinetikai megismerés határai is. Az elôbbi mondatban a hangsúly a teljesen van, mert hiszen igen nagyszámú reakciónak ismerjük alapvetô törvényszerûségeit. Meg tudjuk mondani, hogy meghatározott kezdeti feltételek esetén mi lesz a különbözô idôpillanatokban jó néhány komponens koncentrációja. Ezek az ismeretek elegendôek a kémiai reakciók technológiai alkalmazásának kézben tartására is.
Sajnos sokkal nehezebb, esetleg éppenséggel megoldhatatlan a feladat, ha a reakció során változnak a reakció körülményei, például a hômérséklet, a nyomás, fotokémiai reakció esetében a megvilágítás erôssége, heterogén reakciók esetében a különbözô fázisok minôsége és mennyisége stb.
 |
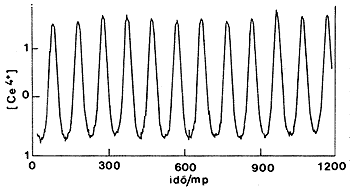
| 1. ábra. A fényelnyelés változása
az idô függvényében a bromát malonsav Ce(IV) rendszerben |
Különösen nehéz a kémiai események idôbeli lefolyásának leírása bizonyos visszacsatolási jelenségek esetében. Nevezetesen, számos reakció során jelentkezik a reakció termékeinek jelentôs kinetikai hatása. Ha a termék(ek) a reakció sebességét növelik, akkor autokatalízissel, ha pedig csökkentik, akkor autoinhibícióval van dolgunk. Ilyen esetekben a szokásosnál sokkal hirtelenebb és nehezebben számítható koncentrációváltozások állnak elô. Bizonyos feltételek teljesülése esetén pedig egyes komponensek koncentrációiban egynél több, esetenként igen nagy számú szélsôérték jelentkezhet. Ezek az úgynevezett exotikus reakciók. Egy oszcillációs koncentrációváltozást mutat be az 1. ábra.
Noha a szóban forgó reakció kinetikája nagyon bonyolult és még fontos vonásai sincsenek mind feltérképezve, meghatározott kísérleti feltételek esetén jól reprodukálható kísérleti görbéket kapunk, és a közelítôleg érvényes mechanizmus alapján ki tudjuk számítani, hogy adott idôpillanatban mi lesz a legfontosabb komponensek koncentrációja. Gyakran elôfordul, hogy a koncentrációidô görbék nem szabályosak, inkább a zajgörbékre emlékeztetnek. Ez az ún. kémiai káosz esete (2. ábra). Ilyenkor a koncentrációváltozásokat csak a differenciálegyenletek bonyolult rendszerével írhatjuk le, és ezek a változások rendkívül érzékenyen függnek a kezdeti feltételektôl, illetve azok igen kis mérvû megváltozásától.

2. ábra. A fényelnyelés változása
az idô függvényében ugyanebben a rendszerben,
kisebb kénsav-koncentációk esetén. A kénsav
koncentrációja: a) 0,844 M, b) 0,733 M, c) 0,474 M
Az idôjárás elôrejelzése
Ez a téma mindenkit a legközelebbrôl érdekel, és bár hosszú múltra tekinthet vissza, ma már világosak az elôrejelzés áthághatatlan korlátai. A sok népi idôjárási szabály sokszor jól mûködik, de gyakran mond csôdöt. A meteorológiai elôrejelzés az utóbbi évtizedek során sokat fejlôdött, elsôsorban a meteorológiai mûholdak adatainak az elemzése révén. Azonban az is nyilvánvalóvá vált, hogy a légköri változások jellegzetes kaotikus rendszerben mennek végbe, azaz kicsiny, elôre kiszámíthatatlan változások a várthoz képest igen jelentôs változásokat eredményezhetnek. Azt csak teljesen tájékozatlanok vélhetik, hogy hosszú távra érvényes olyan elôrejelzéseket tehessenek, ami a nyilvánvalóan várhatóakat (ti. hogy nyáron lesz meleg lesz, télen pedig hideg) lényegesen meghaladhatja. A "tudományos", ámde minden alapot nélkülözô idôjárási szabályok kiirthatatlanok. Lakits Ferenc 1890-ben világosan bizonyította, hogy a híres-hírhedt Falb-féle kritikus napok szabálya teljesen alaptalan, és a Holdnak a légkörre gyakorolt árapályhatása olyan kicsiny mértékû, hogy annak az idôjárás alakulására semmiféle hatása nem Iehet. Már hosszú ideje hozzák forgalomba a Dávid-féle idôjárási elôrejelzéseket, melyek Falb elméletének újrafelfedezésén alapulnak. A legfontosabb hosszú távú meteorológiai elôrejelzésre a következô módszer ajánlható. Ábrázoljuk a hômérséklet értékének vagy a csapadék mennyiségének átlagos változását az egész évre. Azután vegyünk egy ceruzát, esetleg golyóstollat, és reszketô mozgással menjünk végig a görbén. Némi gyakorlat után már behunyt szemmel is az említett elôrejelzés pontosságának megfelelô prognózist készíthetünk.
A tudományos elôrejelzés és korlátai
Minden tudományos elmélet legfontosabb próbaköve, hogy milyen mértékben képes addig nem ismert jelenségek és törvényszerûségek elôrejelzésére, azaz, hogy milyen nagy a prediktív ereje. A periódusos rendszer felfedezése módot adott addig nem ismert elemek létezésének feltételezésére, sôt azok tulajdonságainak megjövendölésére is. A Mengyelejev feltételezte ekaelemeket hamarosan fel is fedezték. Az atommáglya megépítése során elméleti úton igen jó közelítéssel számították ki az urán-235 kritikus tömegét. A relativitás elméletének nagy fegyverténye volt a nagy tömegeknek a fény elhajlását elôidézô hatásának elôjelzése, melyet az 1919. május 29-ei napfogatkozáskor igazoltak.
A természet törvényei persze felfedezésük elôtt is ugyanúgy mûködnek, az új felfedezés "csak" azt teszi lehetôvé, hogy tudatosan keressék megnyilvánulási formáit. A kémiai reakciók természetére vonatkozó hatalmas ismeretanyag birtokában igen nagy valószínûséggel megtervezhetô egy addig ismeretlen molekula szintézise. Azt azonban természetesen nem lehet megmondani, hogy egy adott vegyületet mikor állítanak elô, mert a prediktív erô csak a lehetôség mégoly nagy valószínûségû, esetleg teljes bizonyosságú megadását jelenti, de az kívül esik a tudományos vizsgálódás hatókörén, hogy ténylegesen sor kerül-e az eseményre. Ezt ugyanis számos, tudományosan elôre nem látható tényezô nevezetesen: szükséges-e a szóban forgó vegyület elôállítása, megéri-e a költséget, rendelkezésre állnak-e az összes szükséges feltételek stb. is meghatározza.
A különbözô folyamatok idôbeli lejátszódásának leírása tulajdonképpen csak akkor lehetséges, ha a jövô nem más, mint a megismételt múlt. A kémiai reakciók esetében a koncentrációváltozások idôbeli változásának megadása lényegében csupán a reprodukálhatóságot jelenti. A reprodukálhatóság legfontosabb feltétele a törvényszerûségek helytôl és idôtôl való függetlensége, invaranciája. Az égitestek jövôbeli helyzetének megadása pusztán azoknak a ciklikus változásoknak a megfelelô pontosságú ismeretét igényli, melyeket hosszú ideje követnek a csillagászok. Az elôbbi mondatokban a csupán és pusztán jelzôk mögött hatalmas erôfeszítések és eredmények húzódnak meg. Az üstökösök ismételt megjelenését is nagy pontossággal jelzik elôre a csillagaszok, de nem képesek egy meteor becsapódását elôre jelezni. Ez ugyanis nem ismétlôdô, hanem egyszeri jelenség, amely teljesen jelentéktelen hatással van az ismétlôdô csillagászati eseményekre.
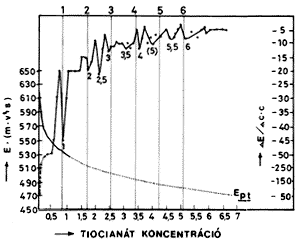 |
| 3. ábra. A redoxipotenciál változása
a vas(III)- tiocianát rendszerben a tiocianátkoncentráció függvényében. Az (a) görbe pontjai csaknem teljesen pontosan illeszkednek egy monoton csökkenô görbéhez,a (b) görbén a DE/DC értékek vannak feltüntetve. A differenciagörbe szélsôértékeihez, melyek egyértelmûen a kísérleti hiba következményei, a szerzôk kémiai jelentést fûztek: a szélsôértékeknek megfelelô összetételû komplexek képzôdnek az oldatokban |
Talán helyénvaló itt az interpolálás és az extrapolálás küzötti alapvetô különbségre felhívni a figyelmet. Az interpolálás esetében meglévô értéksorok hiányzó tagjaira teszünk megállapítást, az extrapolálás esetében pedig a mérési értéktartományon kívül esô értéket számítunk ki. Mindkét esetben feltételezzük bizonyos törvényszerûség, valamely függvénykapcsolat érvényességét. Az interpolálásnak is vannak csapdái, amint ez világosan kiderül a 3. ábra görbéibôl. Vonzódunk az egyszerû összefüggésekhez, a pontsorokon keresztül fektethetünk egy egyenest, a görbe feletti és alatti pontok szépen kiegyenlíthetôk. Eldöntendô, elsôsorban megfelelô pontosságú kísérletekkel, hogy a pontok eltérése az egyenestôl a kísérleti hibának tulajdonítható, vagy pedig a szélsôértékek sorozatának megjelenése valós, és ilyen esetekben a megfelelô értelmezést kell megtalálnunk.
Természetesen nem ilyen egyszerû a helyzet az extrapolálás esetén, hiszen ehhez általában éppen olyankor folyamodunk, amikor a kísérleti meghatározásuknak az adott értéktartományon kívül akadálya van. Ha az értékek éppen az idô függvényében változnak, akkor az extrapolálás tulajdonképpen a jövô egy szeletének megbecslését, ha úgy tetszik, megjövendölését jelenti. Míg az interpolálás helyessége csak azt követeli meg, hogy az alkalmazott törvényszerûség az adott értéktartományon belül legyen érvényes, addig az extrapoláláskor fel kell tételeznünk, hogy a mennyiségi összefüggés teljesül az értéktartományon kívül is. Az extrapolálás könnyen vezethet teljesen képtelen eredményre akkor is, ha az alapösszefüggés érvényes ugyan, de eltekintünk azoktól a feltételektôl, melyeket érvénye megkövetel, illetve olyan tényezôktôl, melyek meghatározó hatással vannak az események alkulására.
A legegyszerûbb példa a baktériumok szaporodásának nem körültekintô leírása. Egy baktérium osztódási ideje 2030 perc. Tehát a leglassabb szaporodás esetén a baktériumok száma 2n, ahol n az idôt jelenti órában. Egy nap múlva a baktériumok száma 224, egy hét múltán pedig 2168. Mivel 1015 darab baktérium átlagos tömege 1kg, ez azt jelenti, hogy egyetlen darab baktériumhol 1 hét alatt kereken 4 x 1035 kg tömegû baktérium keletkezik, ami éppen tíz Nap tömegével egyenlô. Nyilvánvaló ennek a számításnak a képetelen volta, hiszen eltekintettünk a baktériumok pusztulásától, a tápanyagszükséglet kielégítésétôl, hogy csak a legfontosabbakat említsük. Az elôbbi mondatban tehát a "keletkezik" helyett értelemszerûen "keletkezhetne, ha az összes, egyébként teljesíthetetlen feltételek teljesülnének" írandó. Bármennyire gyermeteg is a példa, hasonlóval nemegyszer találkozhatunk naiv futurológiai megfontolások során.
Bár már többször is említettük, ismét hangsúlyoznunk kell, hogy az elôrejelzés lehetôsége igencsak korlátozott a kaotikus rendszerek esetében, mert a feltételek ugyan egyértelmûen meghatározzák a késôbbi történéseket (innen a determinisztikus káosz kifejezés!), nem tudunk olyan pontosságú kiindulási adatokra szert tenni, melyek lehetôvé tennék az események elôrejelzését.
A futurológia
A futurológiának is sok ága van, hiszen foglalkozhat egyes területek jövôjének kérdéseivel, a különbözô társadalmi változások elôrejelzésével és globális problémákkal. Itt csak néhány kérdés vázlatos tárgyalását tehetjük meg.
A tudományos eredmények elôrejelzésével kapcsolatban idézzük a neves sci-fi író, Arthur C. Clarke "törvényét", mely szerint "Amikor egy kiváló, de idôsödô tudós valamirôl azt állapítja meg, hogy lehetséges, majdnem bizonyos, hogy igaza van. Amikor azonban azt a megállapítást teszi, hogy valami lehetetlen, akkor nagyon valószínû, hogy téved". Természetesen bizonyos, hogy sok kiváló tudós tévedett már annak megítélésében, hogy tudományosan mi lehetséges és mi nem. A leghíresebb példa Simon Newcomb tévedése, aki a Wright testvérek repülése elôtt néhány héttel azt írta, hogy a levegônél nehezebb szerkezettel nem lehet a levegôbe emelkedni. A tudósok konzervativizmusa valóban ismert jelenség, de együtt jelentkezik más tudósok forradalmian új elképzeléseivel. A tudomány egészséges fejlôdése a két magatartás egyensúlyán alapul.
A globális futurológiának egyik legjelesebb úttörôje volt Gábor Dénes. Szerinte a civilizációt három nagy veszély fenyegeti: a nukleáris háború pusztítása, a túlnépesedés és a Henyélés Korának az eljövetele. A nukleáris háború veszélye ma kisebbnek laítszik, mint egy évtizeddel ezelôtt, a túlnépesedés problémája továbbra is fenyeget, de a Henyélés Korától talán még messze vagyunk.
Minden futurológiai megfontolásnak figyelembe kell vennie, hogy a fejlôdésnek, illetve a növekedésnek áthághatatlan korlátai vannak: nyersanyagkészletünk nem kimeríthetetlen, az élelem termelése szükségképpen korlátozott. Minden olyan fantáziálás, ami a földi kultúra kozmikus kiterjesztésével akarja a korlátokat ledönteni, képtelennek tûnik. Bele kell nyugodnunk, bogy minden földi problémát itt kell megoldanunk.
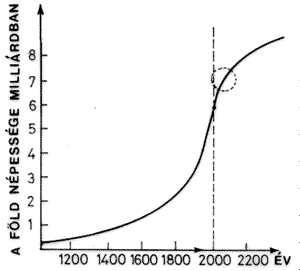 |
| 4. ábra. A Föld népességének változása az idô függvényében |
A növekedés korlátaira legerôteljesebben az ún. Római Klub mutatott rá. Bár az események alakulása nem követte a híres könyv, "The limits of growth" elôrejelzését. Az nyilvánvaló, hogy a növekedésnek vannak korlátai: az emberiség lélekszáma, az energiaigény, a nyersanyagtermelés stb. nem folytatódhat hosszú idieg az eddigi exponenciális módon, a növekedés ütemének szükségképpen lényegesen csökkennie kell, sôt nem pusztán a növekedés üteme, de maga a növekedés is korlátozott. Az említett jellemzô mennyiségek idôbeli változását nem az exponenciális, hanem az ún. logisztikus görbe írja le, melynek az a jellemzôje, hogy egy lassú kezdeti szakaszt követôen meredek növekedés, majd ismét egy lassú, esetleg igen lassú növekedés, sôt állandósulás következik. Ilyen görbével írható le pl. az emberiség létszámának növekedése.
A 4. ábrából kitûnik, hogy milyen mértékben csökkent a népesség számának megkétszerezôdéséhez szükséges idô, és a 2000-re extrapolált érték kereken 6 milliárd. Bár az nagyon vitatható, hogy számszerûen legfeljebb hány ember élhet a Földön, az aligha kétséges, hogy van ilyen határérték, azaz a görbe nem folytatódhat exponenciálisan, hanem el kell laposodnia. Bizonyossággal állítható, hogy nem kerülhet sor további kettôzôdésekre, azaz a 4. ábrán, valahol a körrel jelzett szakaszban a növekedési görbének el kell laposodnia.
Prekogníció és jóslás
Talán célszerû lesz különbséget tenni a parapszichológiai prekogníció és a különbözô jóslási módok között, bár a két fogalom valójában elválaszthatatlan egymástól. Az egyértelmûség céljából röviden meghatározzuk a négy parapszichológiai alapjelenséget: a telepátia vagy gondolatátvitel két személy közötti, az ismert érzékszervek közvetítése nélküli kapcsolatot jelent; a tisztánlátás (clairvoyance) csetében az adott személy egy eseményrôl, vagy helyrôl anélkül szerez tudomást, hogy érzékszerveit használ(hat)ná, de ebben nem valamely másik személlyel való telepatikus kapcsolata segíti; a prekogníció valamely esemény elôre való ismerete; a pszichokinézis pedig valamely anyagi folyamat befolyásolása pszichikai úton. A két utóbbi jelenség kapcsolatban lehet egymással. Ha ugyanis például kockadobási kísérleteket csinálunk, a prekogníciót az jelentené, hogy a várható statisztikus elôfordulást meghaladó arányban mondja meg a kísérlet alanya a következô dobások eredményét. A sikeres kísérlet esetében azonban nem zárhatnánk ki azt a lehetôséget sem, hogy a kockák helyzetét változtatja meg a kísérlet alanya gondolati úton. Az elmúlt néhány év során sok ilyen kísérletet végeztek, kezdetben valóban kockadobással vagy különhözô, a kísérletek céljaira kidolgozott kártyákkal, azután pedig számítógépekkel. Az elvégzett nagyszámú kísérlet nem hozott egyértelmû eredményeket. Az kétségtelen, hogy még a legjelentôsebb prekogníciós eredmények is csak a finom statisztikus módszerekkel mutathatók ki. Hozzátehetjük, hogy még ezeket a szignifikancia határát súroló eredményeket is vitatják, és független kísérletezôk által való megerôsítésük még várat magára. Az azonban nyilvánvaló, hogy még a legsikeresebb prekogníciós kísérlet sem tekinthetô akár a legszerényebb igényeket kielégítô jóslásnak sem. A prekognitív sztárok, mint Peter Hurkos, vagy Uri Geller szenzációs jövendölései egytôl egyig utólagosan születtek. Egy jelentôs esemény megjövendölésérôl írni hálás és könnyû dolog: a jövendölés alaptalanságának kimutatása, ti. hogy az valóban az esemény elôtt született, fáradságos újságírói nyomozómunkát igényel, és az eredmény nem szenzációs, hiszen senki sem figyel fel arra, hogy X jósnak nem sikerült a jövôt megmondania. Pedig milyen egyszerû lenne a jövôbe látás képességét meggyôzôen bizonyítani. Mindössze háromszor egymás után kellene bankot robbantani a monte-carlói kaszinóban, de el sem kellene Monte-Carlóba utazni, elegendô lenne valamelyik budapesti játékkaszinóban ezt megcsinálni, vagy háromszor egymás után ötös találatot elérni a lottón. (A háromszor egymás után megszorításra a koincidencia kizárása miatt lenne szükség, de e sorok írója már egyetlen elôre bejelentett (átvitt értelmû!) bankrobbantás vagy ötös találat esetén is gondolkodóba esne, és hajlandó lenne kétkedését feladni.).
A folytatásban a különbözô jósló eljárásokat ismertetjük.
| Természet Világa, | 129. évf. 1. sz. 1998. január, 1619. o. |
| https://www.kfki.hu/chemonet/TermVil/ | |
| https://www.ch.bme.hu/chemonet/TermVil/ |