Bolyai János az abszolút geometria megalkotásával korszakalkotó felfedezést tett a matematikában. A zseniális geométer nevét az egész világ ismeri és becsüli. Könyvtárnyi Bolyai-írás, -méltatás, köztük számos rangos monográfia jelent meg életérõl és munkásságáról. A korábbi Bolyai-kutatók véleménye szerint Bolyai János híres mûvének, az Appendixnek publikálása után végzett ugyan más, nem geometriai tárgyú kutatásokat is, ezekkel azonban nem ért el érdemleges eredményeket.

  Kiss Elemér marosvásárhelyi matematikaprofesszor Bolyai-kutatásaival és -könyvével tudománytörténeti szenzációval szolgál. A szerzõ a marosvásárhelyi Teleki–Bolyai Könyvtárban található publikálatlan Bolyai-hagyaték többéves kitartó, aprólékos tanulmányozása, a több ezer oldalt kitevõ feljegyzések szakértõ elemzése után arra a meglepõ eredményre jutott, hogy Bolyai János a saját korában jelentõsnek számító algebrai és számelméleti problémákkal is foglalkozott, s mai szemmel is igen figyelemre méltó tudományos eredményeket ért el ezeken a területeken. Bár ezen eredmények jelentõsége nem mérhetõ össze Bolyai geometriai felfedezésével, megszületésük idején – ha ismertté válnak – fontos hatást gyakorolhattak volna az algebra és a számelmélet bizonyos ágainak fejlõdésére. Bolyai említett, mindeddig nem ismert eredményeit mostanáig más matematikusoknak tulajdonították, mivel azokat Bolyaival lényegében egyidejûleg vagy késõbbi idõkben mások is felfedezték és publikálták. Mostoha sorsa miatt Bolyai saját írásaiból csupán a 26 oldalas Appendixet láthatta nyomtatásban. Felvetõdik a kérdés, hogy mi mindennel gazdagíthatta volna még a matematika tudományát ez a géniusz, ha kedvezõ körülmények között folytathatta volna kutatásait és publikálta volna felfedezéseit.

  Kiss Elemér nemes feladatot teljesít, amikor szakavatott módon tárja elénk és adja közre Bolyai eddig nem ismert algebrai és számelméleti vizsgálatait és azok eredményeit. Ezzel nagy mértékben járul hozzá a Bolyai-hagyatékban még mindig létezõ fehér foltok eltüntetéséhez, valamint az eddig ismertnél árnyaltabb, teljesebb, színesebb Bolyai-kép kialakításához.

  A szerzõ olvasmányos formában, élvezetes stílusban, de mindvégig szigorú tudományos igényességgel fejti ki mondanivalóját. Az I. fejezetben felidézi Bolyai életútját, szót ejt geometriai felfedezésérõl és egyéb ismert kutatásairól. A II. fejezetet a Bolyai-ládáknak szenteli, melyek a Bolyai-feljegyzéseket, a kéziratos hagyatékot tartalmazzák. Az Appendix 1831-es megjelenése nem hozta meg Bolyai János számára a megérdemelt elismerést. Bolyai élete második felét a világtól elzárva, csalódottan, erdélyi magányában töltötte. Szinte élete végéig folytatta matematikai kutatásait, s mint írja, élvezte a kutatás örömét. Matematikai feljegyzéseit saját maga számára készítette, gondolatait egyedül apjával, Bolyai Farkassal, a neves matematikaprofesszorral osztotta meg levelezés formájában. Feljegyzéseit magyar, német és latin nyelven írta különféle papírokra, borítékokra, hivatalos dokumentumokra, szinte mindenre, ami keze ügyébe került. A feljegyzéseken sok a betoldás, áthúzás, a félbeszakadt szöveg. Mondanivalóját sokszor más lapokon folytatja, vagy csak következtetni lehet arra, hogy a folytatás a hagyaték egy részével együtt elveszett.

  Mint Kiss Elemér könyvében rámutat, a feljegyzések olvasását az is nehezíti, hogy Bolyai János gyakran sajátos, az elfogadottól eltérõ jelöléseket és terminológiát használt. Ezzel is magyarázható, hogy bár a Bolyai-hagyatékot ezt megelõzõen többen végigolvasták, a korábbi Bolyai-kutatóknak nem sikerült az algebrai és számelméleti eredményekre rábukkanniuk. A hagyaték ilyen vonatkozású megszólaltatásához az kellett, hogy egy lelkes algebrista Bolyai-kutató, Kiss Elemér több évet eltöltsön a Teleki Tékában, felismerje a különbözõ papírlapokon található feljegyzések közötti matematikai összefüggéseket, s feltárja azok igazi matematikai mondanivalóját.

  A könyv III. fejezete Bolyai János matematikai olvasmányairól, matematikai mûveltségérõl szól. A szerzõ megismerteti az olvasót, hogy Bolyai élete második, magányos munkálkodással eltöltött részében honnan és hogyan merítette matematikai ismereteit. Kapcsolatot csupán apjával tartott, a világtól elzártan, más matematikusoktól függetlenül végezte kutatásait.

  Tudománytörténeti szempontból a könyv legértékesebb, legeredetibb része a IV., az V. és a VI. fejezet, melyben a szerzõ Bolyai János számelméleti és algebrai vizsgálatait és azok eredményeit ismerteti. Az alábbiakban ezekrõl ejtünk néhány szót.

  Bolyai János fontos eredményekre jutott a prímszámok tanulmányozásakor. Ha p prímszám és a p-vel nem osztható egész szám, úgy a kis Fermat-tétel szerint p|a^p–1–1. Apja ösztönzésére János megkísérelte bebizonyítani a tétel fordítottját, ami azt eredményezte volna, hogy a tétel prímkritérium. Hamarosan rájött azonban, hogy ez nem lehetséges, mivel 341|2³⁴⁰–1, holott 341=11·31 összetett szám. Ezzel az elsõ ún. pszeudoprímszámot találta meg. Matematikatörténeti kutatások alapján ma már tudjuk, hogy ezt egy ismeretlen szerzõ valamivel korábban, Bolyaitól eltérõ módon bebizonyította és publikálta, errõl azonban Bolyainak nem volt tudomása. Általánosabban, Bolyai módszeres eljárást dolgozott ki az olyan különbözõ p, q prímszámok keresésére, melyekre pq|2^pq–1–1 teljesül, azaz amelyekre p·q pszeudoprím. Több mint 40 évvel késõbb ezt egy Jeans nevû matematikus újra felfedezte, azóta a tételt Jeans-tételként ismeri a matematikai szakirodalom. Bolyai azt is megmutatta, hogy a nevezetes F₅ = 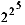+1 Fermat-féle szám pszeudoprím. Érdemes megjegyezni, hogy a pszeudoprímek kutatása csak jóval Bolyai János halála után, 1876-ban indult meg. Bolyai kezdeményezõje lehetett volna ennek a problémakörnek.

  Gauss egyik nagy matematikai felfedezése a késõbb róla elnevezett Gauss-egészek (a+bi alakú számok, ahol a, b egészek és i= ) aritmetikájának kidolgozása volt. Bár Gauss és Bolyai Farkas idõnként leveleztek, Gauss ezen eredményei nem jutottak el a Bolyaiakhoz. Mint Kiss Elemér a hagyaték alapján könyvében kimutatja, Bolyai János Gausstól függetlenül és lényegében vele egyidejûleg szintén kidolgozta ezen számok, az általa komplex egészeknek nevezett számok oszthatósági elméletét, és feltárta az összes komplex prímeket. Ez tekinthetõ Bolyai János legértékesebb számelméleti eredményének. Mint Bolyai feljegyzéseibõl kiderül, az általa prímtannak vagy imaginárius számelméletnek nevezett elméletét publikálni is akarta, sajnos azonban erre nem került sor. Bolyai elméletét nem csupán kidolgozta, annak alkalmazásait is adta. Egyebek között több szép és új bizonyítást adott Fermat azon híres tételére, mely szerint bármely 4k+1 alakú prímszám elõáll két négyzetszám összegeként. Bolyai ún. 4. bizonyítása minden idõk egyik legszebb és legrövidebb bizonyítása a tételnek.

  Mindezek után joggal állapítja meg Kiss Elemér könyvében, hogy az eddigi vélekedéssel ellentétben a magyarországi számelméleti kutatások valójában a Bolyaiakkal kezdõdtek.

  Bolyai János korában több évszázados nyitott kérdés volt az algebrai egyenletek gyökképlettel való megoldhatóságának problémája. n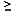5 esetén hosszú ideig hiába keresték az n-edfokú algebrai egyenlet általános gyökképletét. Ruffini 1799-ben publikált egy bizonyítást, mely szerint ilyen gyökképlet nem is létezik. Bolyai János ismerte ezt a bizonyítást, és felfedezte, hogy az hiányos. Ezért elõször õ maga is a gyökképlet keresésén fáradozott. Feljegyzései szerint a kérdés már 1826 óta foglalkoztatta. Késõbb azt írja, hogy Ruffini bizonyításának hibáit kijavította, ilyen gyökképlet valóban nincs. Sõt, mint írja, ezen tételre talált egy másik bizonyítást is. Ezek a bizonyítások sajnos nem találhatók meg a feljegyzések között, valószínûleg elvesztek. Bolyai nem tudott arról, hogy 1826-ban Abel a tételre teljes bizonyítást közölt, s nem ismerte Galois eredményeit sem. Mindenesetre Bolyai feljegyzéseibõl világosan kitûnik, hogy kortársaitól függetlenül õ is eljutott a Ruffini–Abel-tételig és annak bizonyításáig, ami mai szemmel mérve is igen jelentõs matematikai teljesítménynek tekinthetõ.

  A két Bolyai, János és Farkas levelezésébõl a napjainkig feltárt levelek csak elvétve tartalmaznak matematikai szövegrészeket. A könyv VII. fejezete a Bolyaiak levelezésébõl 18 matematikai tárgyú levelet tesz közzé, melyek – három levél egyes részleteinek kivételével – eddig kiadatlanok voltak. A levelek közül négyet Farkas küldött Jánoshoz, a többit pedig János írta apjának. A legtöbb levél számelméleti kérdésekkel foglalkozik.

  Mint már említettük, Bolyai János gyakran eltért az õ korában már elfogadott és alkalmazott elnevezések és jelölések használatától. Ezzel sajnos nagyon megnehezítette kéziratos hagyatékának olvasását. A VIII. fejezet a Bolyai által használt sajátos mûszavak és jelölések jegyzékét és magyarázatát tartalmazza. Ezáltal a szerzõ azok munkáját kívánja megkönnyíteni, akik a jövõben is tanulmányozni szeretnék Bolyai írásait.

  Végül a könyv gazdag irodalomjegyzékkel, 130 könyv, tanulmány és más forrásmunka felsorolásával, valamint név- és tárgymutatóval zárul.

  A könyv a Magyar Tudományos Akadémia támogatásával, az Akadémiai Kiadó és a Typotex Kiadó közös kiadványaként jelent meg. A két kiadót külön dicséret és elismerés illeti, amiért a magyar nyelvû változattal egyidejûleg, Mathematical Gems from the Bolyai Chests címmel a könyv angol nyelvû változatát is megjelentette Csirmaz Anikó és Oláh Gábor fordításában. Ezzel Bolyai János most feltárt matematikai kincsei a nagyvilág számára is megismerhetõvé válnak.