
KISS ELEMÉR
Bolyai János kéziratainak rejtett matematikai kincsei
Bolyai János (1802–1860) a magyar és egyetemes tudomány egyik legnagyobb alakja. Népünk szellemi alkotóképessége a tudomány terén legmagasabb fokon benne öltött testet. Életét és munkásságát számos mû méltatta, sokan és szerencsére sokat írtak róla. Az elõttünk járók szorgos munkájának köszönhetõen ma már könyvtárnyi Bolyai-írással rendelkezünk. Tudunk-e hát mindent Bolyai Jánosról? Vannak-e ma, 1997-ben, fehér foltok az abszolút geometria megalkotójára vonatkozó ismereteink térképén?
A következõkben, ezekre a kérdésekre válaszolva megmutatjuk, hogy még napjainkban is lehet újat mondani az Appendix tudós szerzõjérõl. Bolyai János ládái még sok olyan kincset rejtenek, amelyekrõl semmit sem tudtunk. Felnyitva azokat a türelmes kutatónak sok örömben lehet része, amikor ezeket megtalálja.
Bolyai János halálakor sok ezer oldalnyi kéziratot hagyott hátra. Ezek lapjai rejtik azokat a gondolatokat, amelyeket írójuk életének második felében magányosan, sivár környezetben jegyzett föl. A kéziratokat mintegy száz évvel ezelõtt Paul Stäckel tanulmányozta elõször alaposan. Az õ úttörõ munkájának köszönhetõ, hogy a tudományos világ a századforduló idején megismerhette Bolyai János több, kéziratban maradt matematikai eredményét. Érthetõen Stäckel sem végezhetett tökéletes munkát, mindent felölelni és valósan értékelni nem tudott.
Kulturális–tudományos örökségünk feltárásának s ennek keretében a Bolyai-portré minél igazabbá tételének igénye ösztönzött arra, hogy átolvassam, kibetûzzem a marosvásárhelyi Teleki–Bolyai Könyvtárban õrzött sokezernyi Bolyai-kéziratot s megvizsgáljam, mit végzett az abszolút geometria felfedezõje a matematika más területein. Aprólékos, makacs munkám jutalmaként sikerült a “Bolyai-ládák” több új, eddig ismeretlen titkát, távlatát felfednem. Vallatóra fogva ezeket az írásokat, kirajzolódott az ismertnél árnyaltabb, teljesebb Bolyai-kép.
Igaz, hogy a hagyatékban nem találunk a Tér Tudományához hasonlítható mûvet, de ha türelmesek vagyunk és elég mélyre ásunk, akkor felfedezzük, hogy a Bolyai-kéziratok még sok meglepetést tartogatnak számunkra. Fáradozásainkért bõven kárpótolnak azok a kincsek és gondolat-gyöngyök, amelyeket felszínre hozhatunk. Remélem, hogy a kedves Olvasó is annak tekinti majd Bolyai Jánosnak azokat a gondolatait, amelyek eddig a Teleki Téka polcain heverve nem váltak ismertté a matematikai irodalomban, de amelyekre késõbb, évtizedekkel zseniális matematikusunk halála után mások is rátaláltak és különbözõ folyóiratokban publikáltak.
Az alábbiakban, az eddig kiadatlan dokumentumokat felhasználva szeretném néhány helyen egyrészt kiegészíteni a Bolyai Jánosra vonatkozó eddigi ismereteinket, másrészt pedig kiigazítani a korábbi szakirodalom tévedéseit. Elsõsorban azokra a Bolyai-gondolatokra fogok rámutatni, amelyeket aztán az elkövetkezõ korok matematikusai rendre újra felfedeztek.
Egy fontos láncszem
Elõször Bolyai János életútjának eddig jól ismert állomásait egészítjük ki néhány újabb adattal.
Hála Bolyai Farkas (1775–1856) közlékenységének, elég sokat tudunk János gyermekkoráról. A fiára büszke apa ifjúkori barátjához, Gausshoz írott leveleiben részletesen beszámol ezekrõl az idõkrõl. Érdekesek viszont Bolyai Jánosnak azok a késõbbi följegyzései, amelyekben saját maga beszél a matematika iránt már gyermekkorában felébredt vonzalmáról. “Már kisgyermek koromban – írja egy helyen – feltettem magamnak a kérdést, hogy végtelen sok prímszám létezik-e?” Az e számmal kapcsolatban megjegyzi, hogy már fiatal korában átlátta, hogy

Bevallja, hogy eleinte az imaginárius mennyiségek fogalma nem volt elég világos számára, de aztán meglátva az ii=e–p/2 formulát, érdeklõdése azonnal ezek felé a számok felé fordult: “... de akkor még az al-uti nyikról [imaginárius mennyiségekrõl] nekem sem lévén illõ világos képzetem, inkább irtózva s hasztalan üresnek véve elfordultam s annyibahagytam, nem is mertem akkor tovább nyomozni (mint a háromszög-tant is legelõbb bár is észre-véve), míg végre megláttam az ii=e–p/2... mi által végre fölhíva érzem magamat mindenekelõtt a fõ- és al-uti nyikról tiszta fogalmat szerezni”.
Kétségtelen, hogy Bolyai János számára az 1820-as évek az Appendix kidolgozásának jegyében teltek el. Ezzel életrajzának valamennyi írója egyetért. Följegyzései között azonban olyan írásokat is találunk, amelyek arra utalnak, hogy a geometria mellett már ebben az idõben a matematika más ágai is foglalkoztatták. Így például a komplex számok elmélete, a magasabb fokú algebriai egyenletek és a számelmélet is. “Az imaginárius mennyiségek tanát – írja – amikor az én igen fontos Tér Tudományommal foglalkoztam, már kigondoltam”. Két, Aradra címzett kiterített levélborítékon – amelyek közül az egyik 1827. március 11-ei keltezésû – a fiatal katonatiszt a harmadfokú algebrai egyenletek megoldását tárgyalja. Hogy az 1820-as években milyen alaposan tanulmányozta Bolyai Gauss munkáját a Disquisitiones arithmeticae-t, kitûnik apjának Gausshoz írt, 1831. június 20-án kelt levelébõl: “Fiamnak szándéka volt, hogy a Te polygon-elméletedet németül, a kisebb kaliberû elméknek valamivel könnyebben hozzáférhetõ módon adja ki”.
Úgy gondolom, hogy az Appendix végsõ formába való öntése történetének egy igen fontos láncszemét sikerült megtalálnom a kéziratos hagyatékban.
Tudjuk, hogy Bolyai János 1820 és 1824 között összeállította térelméletének anyagát. 1825 elején hazalátogatva Marosvásárhelyre megmutatta apjának a már kidolgozott elméletét, 1826-ban pedig Aradon átadta volt bécsi tanárának, Wolter von Eckwehrnek fölfedezése egy kéziratos fogalmazványát. Bolyai Farkas 1831. június 20-án postázta Gussnak az Appendix “különlenyomatát” [11]. Ezeket az ismert adatokat Bolyai János nyilatkozatai segítségével egy újabbal tudjuk kiegészíteni. Két följegyzésében is tanúsítja, hogy az Appendix már 1829-ben teljesen kidolgozva készen volt. Mindkét helyen arra a tényre hivatkozik, amely szerint a Tentamen kiadásához (amelynek “függeléke” volt Bolyai János mûve) szükséges nyomtatási engedélyt már 1829-ben (pontosan október 12-én) kiadták a hatóságok, akkor pedig a munkának készen kellett lennie: “... a rengeteg sok szükségest magába foglaló – írja Bolyai – és Euklid sõt Ádám óta a tanban a legnagyobbszerû idõszakot kezdett vagy legalább elõkészített Marosvásárhelyt, mint a munka törvényes elõvizsgálata vagy recensiója idõszám vagy határozatából kiviláglik már 1829-ik évben készen volt vagy állott, bár is sokféle más akadályok miatt csak az 1832-ik évben megjelent Tentamen...” (1. ábra). A másik följegyzésben pedig egyebek mellett ezt olvassuk: “És így elég csodálatos, nevezetes és különös az, hogy bár is az Appendix lényegére nézve már 1823-ban megszületett 1829-ben a Tentamen kihirdetés s kinyomtatásra a könyvvizsgáló Bizottságtól szabadságot nyert...”
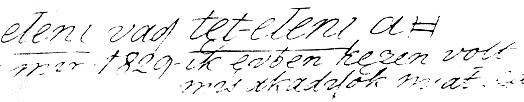
1. ábra. "...már 1829-ik évben készen volt..."
Az 1829-es évet azért kell nyomatékosan hangsúlyoznunk, mert a nemeuklideszi geometria történetét tárgyaló munkák szerint Lobacsevszkijnek az Appendixszel összemérhetõ orosz nyelvû értekezése 1829–30-ban jelent meg.
Bolyai matematikai ismeretei
Életrajzíróinak egyöntetû véleménye szerint Bolyai János matematikai képzettsége a korabeli matematikai ismeretek tekintetében vázlatos volt.
Próbáljuk meg az alábbiakban aprólékosabban megvizsgálni ezt a kérdést, és az eddig ismeretlen dokumentumokat figyelembe véve feltérképezni Bolyai János ismeretanyagát.
Való igaz, hogy a bécsi Akadémián az ún. felsõbb matematikából csak keveset tanult. Domáldi, majd marosvásárhelyi évei alatt igencsak szûkében volt a tudományos segédeszközöknek. Elszigetelt, magányos tudós volt. Korának sok matematikai felfedezése nem jutott el hozzá. Bár kortársa Abelnek (1802–1829), Galois-nak (1811–1832), Eisensteinnek (1823–1852), Riemann-nak (1826–1866), munkásságukról mit sem tud. Nem jutnak el Marosvásárhelyre az akkor már létezõ és színvonalas matematikai folyóiratok. Nem értesül az 1840-ben felfedezett felület, a pszeudoszféra létezésérõl, amelynek egy véges darabján érvényesek a nemeuklideszi geometria tételei. Még Gauss munkásságának eredményeit is csak kis részben ismerte.
Mégis, bármilyen messze volt Marosvásárhely a múlt század derekán a jelentõs matematikai centrumoktól, csak szivárogtak ide is hírek a mathézis világából. Közvetítõjük apja, Bolyai Farkas volt. A kollégium professzora szeretett levelet írni, s ezáltal szoros kapcsolatot tartott fenn Guass-szal és másokkal is. Természetébõl fakadóan csaknem minden iránt érdeklõdött. Minden újságra felfigyelt, s ha valami érdemesnek vagy érdekesnek látszót talált, azt azonnal tudatta fiával. Bizonyára János is elolvasta Gauss leveleit, aki matematikai tárgyú írásai mellett könyveket is küldött Farkasnak.
Szinte hihetetlen, de Gausst is értékes információhoz juttatja Bolyai Farkas. Tõle tudja meg Gauss, hogy megjelent a matematikatörténet egyik fontos, késõbb sokat idézett folyóirata, a Grunert által szerkesztett Archiv der Mathematik und Physik.
Bolyai János (és Farkas) másik forrása a magyar nyelvterület elsõ közkönyvtára, a Marosvásárhelyen 1802 óta mûködõ könyvesház, a Téka. Ez a remek gyûjtemény a Bolyaiak kedvelt szellemi mûhelye. Igaz, hogy a Téka nem szakkönyvtár, de a könyvtáralapító Teleki Sámuel ifjúkorában érdeklõdött a matematika iránt is s így természetes könyvtára matematikai részlegének gazdagsága is. Leibniz 11, Newton 8 munkával szerepel a nyomtatott katalógusban. De jelen vannak a Bernoulliak, Euler, d’Alembert, Lagrange, Clairaut és mások is. A Bolyaiak a Tékában matematikai értekezéseket tartalmazó folyóiratokat is találtak. Olvasták például a Pétervári Actákat (Euler dolgozataival), a Göttingische Gelehrte Anzeigent (Gauss írásaival).
Bolyai János sokat merített apja és a saját maga gyûjtötte matematikai könyvekbõl. Az akkori viszonyokhoz képest mindkettõjüknek gazdag és eléggé jelentõs könyvtára volt.
Talán mégsem volt olyan szegényes és vázlatos Bolyai János szakirodalmi tájékozottsága, amint azt eddig olvashattuk. Igaz, a nemzetközi matematikai kutatás perifériáján dolgozott, de lehetõségeihez képest sokat olvasott. A könyveket, amelyek kezeügyébe kerültek, rendkívüli figyelemmel és igen kritikus szemmel vizsgálta. Jegyzeteiben állandóan hivatkozik olvasmányaira, s ahol okot talál rá, sohasem mulasztja el bíráló megjegyzéseit. Írásaiban sok helyen idézi Lacroix, Lagrange, Laplace, Newton, Cauchy, Bolyai Farkas, Littrow, Mascheroni, Vega, Euler, Montucla mûveit. A legtöbbször Gauss és Ettingshausen nevével találkozunk. A Disquisitiones arithmeticae számos fejezetéhez fûz megjegyzést, Ettingshausen könyvében pedig több hibát felfedez.
Bolyai Jánosnak apjától eltekintve egyetlen olyan tudóstársa sem volt, akivel gondolatait kicserélhette volna. Mégis akadtak a környezetében mûvelt emberek is, akiket tisztelt. Ilyen volt Aradon Wolter von Eckwehr százados és Olmützben Emanuel Zitta õrnagy, akik matematikailag is képzett tisztek voltak. Zitta kölcsönözte Bolyainak a nevezetes Crelle-féle matematikai folyóirat két számát, amelyekben “sok jót” talált. Bolyai mindkét följebbvalóját õszintén tisztelte. Évtizedek múlva sem feledkezett meg róluk. 1851. november 24-én kelt jegyzetében fontos teendõi között megemlíti, hogy “...Wolter – és Zittának írni s Heil-Lehre-met [Üdv-Tanomat] megküldeni”.
Bolyai János tehát tudott arról, hogy a nagyvilágban léteznek matematikai folyóiratok, könyvek, amelyekhez leginkább anyagi okok miatt nem sikerült hozzájutnia.
Ugyancsak fontos feladatai között említi Bolyai “Némi vagy holmi érdekes vagy nevezetes könyvököt, melyek kijötte vagy megjelenése felõl tudomásom van vagy értesültem, csak belátás vagy megnézegetés végett megszerezni”. Szeretné megrendelni nemcsak Gauss s Lobacsevszkij minden mûvét, hanem Ettingshausét is, annak ellenére, hogy ...a már kész Appendix becsét sem volt képes fölismerni...”. Írni akar Kazánba, ismét említi Grunert folyóiratát mint amelyre szüksége van. Külön feladat 1851-ben “Atyáméinak is apróra átnézete”. Jó lenne olvasni még növénytan, állattan, nyelvtan és kristálytannal foglalkozó könyveket is – írja.
Bolyai János nem értesülhetett kora tudományának minden eredményérõl, matematikai mûveltségét mégsem mondhatjuk vázlatosnak. ’ sem volt megelégedve olvasmányaival, sem könyvei számával. Természetesen szeretett volna még többet tanulni. “Eddig elé – jegyzi meg 1856-ban – a legnagyobb szorgalom s képesség mellett sincs mit egyebet tenni... mint néhány hallomás szerint jobb, általján történetesen kezünkbe került könyvrõl is némileg okulni. És valóban: nekem nagyon kevés könyvöm van...”.
Nem fogadhatjuk el tehát a köztudatba eddig eléggé behatolt képet a két Bolyairól. Éppen ellenkezõleg, Vekerdi Lászlónak van igaza, amikor [12] tanulmányában így ír: “Sarlóska Ernõ látja jól, hogy Bolyai János Bécsben egy tág horizontú világba jutott, amibõl késõbb se lépett ki soha. Merõ anakronizmus õt Marosvásárhelyre bezárni. Mindvégig a szellemi Európa ama nagy polgáraihoz tartozik, akik megismerték és vállalták a végsõkig gondolt gondolatok szigorú keménységét... A Bolyaiak – apa és fiú – nem holmi provinciális nyomorba süllyedt s kínjukban egymást tépõ szerencsétlenek; alakjuk és sorsuk az európai gondolkozás fõáramába tartozik, szervesen és kitéphetetlenül. Kihagyásuk az európai szellem egész történetét károsítja és hamisítja meg.”
IRODALOM
[1] Carmichael, R. D.: On composite numbers P which satisfy the
Fermat congruence ![]() .
Amer. Math. Monthly, 19(1912), 22–27.
.
Amer. Math. Monthly, 19(1912), 22–27.
[2] Dickson, L. E.: History of the Theory of Numbers, Chelsea, New York, 1952.
[3] Erdõs Pál: On the Converse of Fermat's Theorem, Amer. Math. Monthly, 56(1949), 623–624.
[4] Jeans, J. H.: The Converse of Fermat's Theorem, Messenger Math., 27(1897–1898), 174.
[5] Kiss Elemér: Fermat's Theorem in János Bolyai's Manuscripts, Mathematica Pannonica, 6(1995), nr. 2, 237–242.
[6] Kiss Elemér: Foglalkozott-e számelmélettel Bolyai János?, Természet Világa, 127(1996), 8. szám, 344–348.
[7] Kiss Elemér: Kérdések Bolyai János kutatásairól, Természet Világa, 127(1996), 11. szám, 522–523.
[8] Kiss Elemér: Bolyai János vizsgálatai a 4m+1 alakú prímszámok két négyzet összegére való felbontásáról, Polygon, Szeged, 6(1996), 2. szám, 1–11.
[9] Lehmer, D. H.: Tests for primality by the converse of Fermat's Theorem, Bull. Amer. Math. Soc., 33(1927), 327–340.
[10] Lehmer, D. H.: On the Converse of Fermat's Theorem, Amer. Math. Monthy, 43(1936), 347–354.
[11] Szénássy Barna: Kérdések és válaszok, Bolyai Jánosra emlékezünk! Születésének 175. évfordulóján, Tudományos Ismeretterjesztõ Társulat Budapesti Szervezete, 1978, Szerkesztette Staar Gyula, 29–40.
[12] Vekerdi László: A Bolyai-kutatás változásai,
Természet Világa, 112(1981), 2. szám, 56–58.
| Természet Világa, | 1998. III. különszám, 16–20. oldal
http://www.kfki.hu/chemonet/TermVil/ http://www.ch.bme.hu/chemonet/TermVil/ |