KISS ELEMÉR
Bolyai János kéziratainak rejtett matematikai kincsei
Elfeledett felfedezések
Meglepõen eredetiek Bolyai Jánosnak a számelméleti problémákkal kapcsolatos gondolatai és eredményei. A Bolyai munkásságát ismerõ olvasónak biztosan különösnek hangzik ez az állítás, ami érthetõ, hisz az eddig megjelent valamennyi Bolyai-monográfia szerzõjének egybehangzó véleménye szerint az abszolút geometria felfedezõje nem vonzódott a számelméleti problémákhoz. Pedig ennek éppen az ellenkezõje igaz. A kézirathagyaték lapjai arról tanúskodnak, hogy a fenti véleményekkel ellentétben Bolyai János igen élénken érdeklõdött a számelmélet nehéz kérdései iránt. Ezekrõl az [5], [6], [8] dolgozatokban már részletesen beszámoltunk. Most – írásainkat újabb adatokkal is kiegészítve – Bolyainak fõképpen azokat az észrevételeit emeljük ki, amelyek kézirataiban rejtõzve nem válhattak ismertté és amelyeket a halála után tevékenykedõ matematikusok újra felfedeztek.
Bolyai János sokat fáradozott a prímszámok
képletének keresésével. Egy idõben úgy
gondolta, hogy ezt a kis Fermat-tételben megtalálhatja. Ez
a tétel azt mondja ki, hogy ha p egy prímszám,
a
egy olyan egész szám, amely nem osztható
p-vel,
akkor az ap–1–1 különbség osztható
p-vel,
amit röviden még a következõképpen szoktunk
írni:
| (1) |
| (2) |
bár 341=11·31. Az olyan összetett p számokat, amelyekre az (1) kongruencia a=2 esetén teljesül, pszeudoprímeknek vagy álprímeknek nevezzük. Ezek szerint 341 egy álprím.
Apja ösztönzésére bolyai megpróbálta bebizonyítani a kis Fermat-tétel fordítottját. Néhány kísérlet után rádöbbent arra, hogy ez lehetetlen. Több olyan összetett p számra talált, amelyekre (1) fennáll.
Bolyai János is felfedezte a legkisebb pszeudoprímszámot, a 341-et. Errõl édesapját 1855 májusában egy levélben értesíti, de a 341-es számot már azelõtt megtalálta. Megemlítjük, hogy ezt a számot egy ismeretlen szerzõ már 1830-ban felfedezte, de Bolyainak errõl természetesen nem volt tudomása.
Érdekes az a mód, ahogyan Bolyai János megtalálta a 341-es számot. Érdemes részletezni az általa “elmélet”-nek nevezett módszert, mert néhány meglepõ megjegyzést fûzhetünk hozzá.
Bolyai azt a kérdést vizsgálja, hogy milyen
feltétel mellett teljesül az
| (3) |
kongruencia, ahol p és q prímszámok, a pedig olyan egész szám, amely nem osztható sem p-vel, sem q-val. Elõször azt veszi észre, hogy
![]()
bármely, a feltételeinket kielégítõ p, q, a számokra teljesül, vagyis
![]()
Ha az
| (4) |
kongruencia igaz lenne, akkor ez utóbbi két összefüggés összeszorzása által nyomban megkapnánk a (3)-at. Tehát most azokat a feltételeket kell megkeresnünk, amelyek ez utóbbi, (4)-es kongruencia helyességét biztosítják.
Ide kívánkozik elsõ észrevételünk.
Feltûnõ azonosság van Bolyai meglátása
és
Erdõs Pál egyik, 1949-ben felhasznált
ötlete között. Ha összehasonlítjuk a fentieket
Erdõs [3] dolgozatával, azonnal szembetûnik, hogy õ
ugyanazt a gondolatmenetet követi, amelyet már Bolyai János
is alkalmazott vagy száz évvel azelõtt (2. és
3. ábra). Még ehhez hasonló gondolatot találunk
D.
H. Lehmer [10] cikkében is.
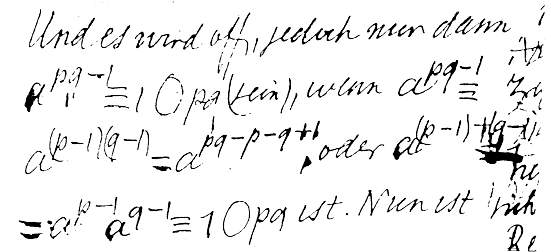 |
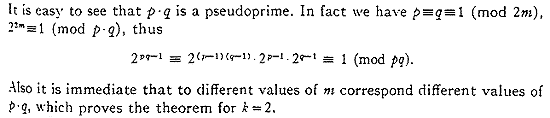 |
2–3. ábra. Bolyai János meglátása és Erdõs Pál 1949-ben felhasznált ötlete között feltûnõ az azonosság
Végül azt találja Bolyai, hogy a (4)-es összefüggés
akkor teljesül, ha
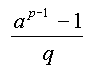 |
és | 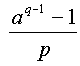 |
(5) |
Az a=2 egyszerû esetben aztán rendre kipróbál néhány, az (5)-ös feltételeket kielégítõ prímszámot, és így eljut a p=11 és q=31 számokhoz, amelyek szorzata 341, s megkapja a (2)-es kongruenciát.
Így fedezte fel tehát Bolyai János a legkisebb
pszeudoprímszámot. Ha módszerét figyelmesen
végigkövetjük, azonnal észrevesszük, hogy
az egy ma már jól ismert tankönyvi tétel. Ugyanis
az (5)-ös feltételek a=2-re így írhatóak:
| és |
vagyis Bolyai szerint, ha ezek a feltételek teljesülnek, akkor azokból a
![]()
kongruencia következik. Ez pedig pontosan J. H. Jeans tétele, amelyet szerzõje 1898-ban, évtizedekkel Bolyai János halála után közölt [4].
Így ez, a Bolyai által felfedezett szép számelméleti tétel ma nem az õ, hanem újrafelfedezõjének nevét viseli. A matematikatörténet-kutatók szerint a matematikai tételek jelentõs része nem az igazi fölfedezõ nevén ismert. A fentiek szerint ezek közé sorolható a Jeans-tétel is. A tételt minden kétséget kizáróan elõször Bolyai János találta meg. Felfedezését – mint oly sok más munkáját az Appendixen kívül – sajnos nem közölte. Ezért rejtõzött évtizedekig a kézirataiban.
A kis Fermat-tétel fordítottjának megcáfolása
sokat foglalkoztatta Bolyai Jánost. A hátrahagyott kéziratokban
több, újabb ellenpéldát találunk erre
a tételre. Megszerkeszti például a
| (6) |
és az érdekes
| (7) |
kongruenciát is.
Egészen egyszerû példa a (6)-os, de nem kis meglepetéssel látjuk viszont egyik D. H. Lehmer által 1927-ben közölt dolgozatban [9]. Bolyai ezt az összefüggést is elmélete alkalmazásaként nyerte. A (7)-es kongruencia bizonyítását azonban másképpen végezte el. Ezt most nem részletezzük, de megjegyezzük, hogy a (7)-hez hasonló, vagyis olyan kongruenciákat, amelyekben az ún. Fermat-féle számok szerepelnek, csak az 1900-as évek elején megjelent dolgozatokban találunk. Bizonyos tehát, hogy Bolyai volt az elsõ, aki kimutatta, hogy F5=232+1 pszeudoprímszám.
A (2)-es összefüggésben szereplõ 341 és a (6)-os összefüggésben szereplõ 15 is két prímszám szorzata. Bolyainak szándékában állt módszerének kiterjesztése arra az esetre is, amikor az ellenpéldáiban elõforduló összetett számok 3 prímszám szorzatára bonthatók, vagyis kereste azokat a feltételeket is, amelyek teljesülése esetén az
![]()
kongruencia is érvényes lesz, ahol p, q, r prímszámok, a pedig olyan szám, amely nem osztható ezek közül egyikkel sem. A célt ebben az esetben nem sikerült elérnie. Próbálkozásait a következõ szavakkal fejezi be: “... de már három tényezõre meglehetõsen vagy elég bonyolult lesz”.
Azért tartjuk mégis feljegyzésre érdemesnek Bolyainak ezt a kísérletét, mert gondolata csak nagyon késõre jutott másoknak is az eszébe. R. D. Carmichael az, aki 1912-ben ilyen kongruenciákat szerkeszt [1].
Sokat foglalkoztatták Bolyai Jánost a fentebb már említett Fermat-féle számok, vagyis az
![]()
alakú számok. A Fermat-féle számok története ugyancsak érdekes és hosszú. Fermat szilárdan hitt abban, hogy az összes ilyen típusú szám prím, noha õ csak az F0, F1, F2, F3 és F4-et számította ki. Sejtése akkor dõlt meg, amikor Euler 1732-ben megmutatta, hogy a következõ Fermat-féle szám, az F5 összetett. Ezután szinte százötven évnek kellett eltelnie, amíg 1880-ban, az akkor 82 éves Landray-nek sikerült tényezõkre bontania F6-ot [2].
A metametika története nem tud arról, hogy 1732 és 1880 között valaki még foglalkozott volna a Fermat-féle számok prím vagy összetett voltának a vizsgálatával. Pedig a mi Bolyai Jánosunk képzeletét is megragadták ezek a számok. Kéziratos hagyatékának számos lapján, kis céduláján, néha más természetû szövegek közé beszúrva, olyan hosszabb, rövidebb jegyzeteket találunk, amelyekben a Fermat-féle számok szerepelnek.
Édesapjához írt egyik levelében például
két helyen is utal a Fermat-féle számokra: “A numerus
perfectus [tökéletes szám], valamint a![]() -re
nézti
elõbbi demonstrációm is egyébaránt jó
és szép...” továbbá: “Azt megmutatni,
hogy bármely 2p–1 idomú szám prím
mihelyt p prím, ugyanakkor, mikor a
-re
nézti
elõbbi demonstrációm is egyébaránt jó
és szép...” továbbá: “Azt megmutatni,
hogy bármely 2p–1 idomú szám prím
mihelyt p prím, ugyanakkor, mikor a ![]() -gyel
bajlódám...”.
-gyel
bajlódám...”.
Sajnos a “jó és szép” bizonyítást
nem sikerült megtalálni a kéziratokban. Egyik helyen
azonban megállapítja és be is bizonyítja, hogy
a ![]() alakú
számok mindig 6n–1 alakúak, következésképpen
sohasem oszthatók 3-mal. Máshol pedig felírja, hogy
alakú
számok mindig 6n–1 alakúak, következésképpen
sohasem oszthatók 3-mal. Máshol pedig felírja, hogy
de az x és y számokról nem állít semmit.
A komplex egészek aritmetikája
A Bolyai-hagyaték nagy kincse a komplex egészek aritmetikája. Lehet, hogy elsõ hallásra túl merésznek hangzik az az állítás, amely szerint a komplex egészek aritmetikáját Gausstól függetlenül és körülbelül vele egy idõben Bolyai János is kidolgozta. Pedig amint a kéziratban maradt jegyzeteibõl kiolvashatjuk, a komplex egészek oszthatóságának minden alapvetõ problémájával foglalkozott. Próbálkozásairól nem készített összefüggõ dolgozatot, de kéziratainak különbözõ oldalairól összegyûjtve a tárggyal kapcsolatos följegyzéseit, belõlük a komplex egészek összefüggõ elmélete bontakozik ki.
A matematikatörténetben a komplex egészek oszthatóságának elmélete Gauss nevéhez fûzõdik, mert eredményeit elõször valóban õ közölte két nagyobb dolgozatban.
A Természet Világa 1996/11-es számában [7] részletesen felsoroltuk azokat az érveinket, amelyek alapján állíthatjuk, hogy Bolyai is felfedezte a komplex egészek minden fontos tulajdonságát. Bár elmélete nem olyan kimerítõ, részletes, mint a Gauss dolgozataiban foglaltak, az alkalmazásokban viszont túlszárnyalta Gausst. Bolyai János a komplex egészekre vonatkozó megállapításait például nagyszerûen felhasználta különbözõ számelméleti tételek bebizonyításánál.
Ragadjunk ki egyetlen példát. Ismert a Fermat-nak
tulajdonított tétel: minden ![]() alakú prímszám a tagok sorrendjétõl
eltekintve egyértelmûen felírható két
egész szám négyzetének összegeként.
Ezt a tételt Bolyai János, felhasználva a komplex
egészeket, a következõképpen bizonyítja:
alakú prímszám a tagok sorrendjétõl
eltekintve egyértelmûen felírható két
egész szám négyzetének összegeként.
Ezt a tételt Bolyai János, felhasználva a komplex
egészeket, a következõképpen bizonyítja:
A Disquisitiones arithmetice 64-es és 108-as pragrafusai szerint, ha p egy 4k+1 alakú prímszám, akkor létezik olyan x egész szám, hogy
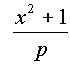
is egész. Ezt a törtet
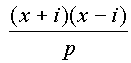
alakba írva következik, hogy p-nek létezik
±1 vagy ±i-vel nem egyenlõ két olyan
komplex egész e és f tényezõje,
amelyekre
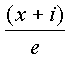 |
és |  |
is komplex egészek. Legyen e = a+bi, f=c+di, ahol a, b, c, d nullától különbözõ egész számok. Mivel p=(a+bi)(c+di), következik, hogy p=(a–bi)(c–di) s akkor p2=p·p=(a2+b2)(c2+d2). De a2+b2>1, c2+d2>1, tehát p=a2+b2=c2+d2.
Bolyai bizonyítását az 1850-es évek közepén egyik, apjához írt levelén jegyezte fel. Fermat tételét elõtte csak G. Eisenstein bizonyította be a komplex egészek segítségével 1844-ben, de ezt a munkát Bolyai nem ismerte. Összehasonlítva Eisenstein bizonyítását [2] Bolyai fenti eljárásával, azonnal megállapíthatjuk, hogy a két bizonyítás lényegesen eltér egymástól. A tétel iránt napjainkban sem szûnt meg a matematikusok érdeklõdése. Az utóbbi évtizedekben, sõt években is több olyan publikáció jelent meg, amelyek szerzõi a Fermat-tétel egyszerû, elemi és minél rövidebb bizonyítására törekedtek, de Bolyai János “demonstrációjának” eleganciáját az elmúlt 140 év dacára – úgy érzem – senkinek sem sikerült elérnie.
Az algebrai egyenletek
megoldhatósága
A Bolyai-hagyaték számos oldalán találkoztunk Bolyai Jánosnak az algebrai egyenletek megoldhatóságával kapcsolatos jegyzeteivel. Följegyzéseibõl és a töredékekbõl tiszta kép tárul elénk ez irányú törekvéseirõl. Kiolvashatjuk belõlük, hogy sokáig bizonytalan úton járva az ötödfokú, sõt a tetszõleges fokszámú algebrai egyenletek megoldását keresi, majd ráébredve tévedéseire õ is eljut a Ruffini–Abel-tételig.
Bolyai néhány, az 1820-as évekre esõ kísérlet után 1837-ben, tehát a domáldi “remeteség” idején kezd az algebrai egyenletekkel alaposabban foglalkozni. Tehát amikor a négynél magasabb fokú egyenletek megoldására vonatkozó gondolatait papírra veti, a matematikusok már ismerik a Ruffini–Abel-tételt. Ezúttal Bolyai egy már megoldott feladattal birkózik. Bár kortársa Abelnek és Galois-nak, amit már megjegyeztünk, munkásságukról nem tud.
Bolyai János érdeklõdését a feladat iránt bizonyára J. Lagrange, Gauss és A. Ettingshausen munkái keltették fel. Gaussról följegyzi, hogy a Demonstratio nova “remek” munkájának a 9. §-ában azt írja, hogy az algebrai egyenletek általános föloldására “csekély remény maradt” és “... Nem több reménnyel nyilatkozik a Disquisitiones arithmeticae 645 lapján” sem. Ettingshausen bécsi egyetemi tanárnak a Teleki Tékában ma is meglévõ könyvében viszont megtalálja Ruffini 1799-ben közölt bizonyítását, amelyben Ruffini “... kísérletet tett a lehetetlenségre nézve... De ezen kísérletbe néhány hiba csúszott be.”
Bolyai tehát észrevette, hogy Ruffini bizonyítása hibás s ebbõl arra következtet, hogy a magasabb fokú egyenletek megoldása nem lehetetlen. Nem ismerve Abel munkáját, elõször õ is – mint olyan sokan mások – az ötödfokú egyenlet megoldását keresi. Egy idõ után aztán rádöbben kísérletei hiábavalóságára, sikerül kijavítania a Ruffini-tétel hibáit, és ezáltal meggyõzõdik arról, hogy a négynél magasabb fokú algebrai egyenletek algebrai úton általában nem oldhatók meg.
Sajnos errõl csak töredékes följegyzései vannak Bolyainak, de ezekbõl is világosan kiolvashatjuk, hogy sikerült végül is meggyõzõdnie a Ruffini–Abel-tétel helyességérõl. Egyik helyen ezt írja: “Tan. [Tétel] Négynél fölsõbb vagyis legalább ötrangú (geber) [ötödfokú, algebrai] általános egyenletet geberül [algebrailag] föloldani lehetetlen”. Ugyanezt fejezik ki fiának, Bolyai Dénesnek 1851-ben készült írásgyakorlatára odavetett sorai: “Véghatározat vagy ultimátum. Az 5-'s fölsõbb rangú egyenlet általános föloldása lehetetlenségét két módon tudom megbizonyítani, úgy mint: a Ruffini illõleg megjavított s tökélyre vitt szép, eredeti, elmés eszméje szerint; és hogy az fm számok 5-gyök-függvény csoportjait nem lehet 5-nél alsóbb (kisebb) rangú egyenlet által meghatározni, vinni. A legtöbb és szebb tehát, mit itt meg lehet tenni és kívánni, megkísérteni: hogy ily...”. Kár, hogy a papír elfogyott, a folytatást pedig nem találjuk.
Megfejtetlen írások
Századunk folyamán nagy számú kutató vizsgálta már Bolyai gondolatait. A kéziratos hagyaték teljes feldolgozása azonban még mindig késik. Munkámmal az utókor e mulasztásának egy részét próbálom pótolni. Úgy érzem, sikerült felfedni a kéziratok sok titkát s másokat is búvárkodásra sarkallni.
A kéziratokban még sok, a matematika más ágaihoz tartozó, megfejtetlen írás található. Van tehát még keresnivalója a tudománytörténésznek Bolyai János matematika tárgyú publikálatlan kéziratai között. Ezek meggyõzõen mutatják, hogy Bolyai János nem kizárólag a geometriában alkotott nagyot. Kora matematikájának minden ága érdekelte, sokoldalú, eredeti tudós volt.
Amint rámutattunk, nem mindig ismerte kortársai felfedezéseit. Fájdalom, a kézirataiban rejtõzõ eredményeirõl sem tudott senki más apján kívül. Pedig ha alkalma lett volna ezeket különbözõ folyóiratokban – melyek már akkor léteztek s amelyekrõl õ is tudott – közzétenni, akkor ma a nevét nemcsak a geometriai, hanem az algebrai, a számelméleti és más szakkönyvekben is gyakran megtalálhatnánk.
Fejtegetéseink során azt is tapasztalhattuk, hogy Bolyai az 1850-es években több matematikai tételt fedezett fel, ami azt jelenti, hogy idõskorában, betegen is, fáradhatatlanul dolgozott. Élete utolsó éveiben is tiszta fejjel gondolkozott matematikai problémákon, a matematikai kutatás örömét és gyötrelmét akkor sem hagyta abba.
Ezért így módosítanám Benkõ Samu szép mondatát: “Bolyai János a matematika fejezetein töprengve élete végéig megõrizte a gondolkodás örömét.”
Köszönöm a Magyar Tudományosság Külföldön akadémiai program keretében meghirdetett Domus Hungarica Scientiarum et Artium ösztöndíjpályázatának támogatását, amelynek segítségével hosszabb idõt tölthettem Budapesten. A dolgozatban szereplõ számos adatot budapesti könyvtárakban találtam meg.
IRODALOM
[1] Carmichael, R. D.: On composite numbers P which satisfy the
Fermat congruence ![]() .
Amer. Math. Monthly, 19(1912), 22–27.
.
Amer. Math. Monthly, 19(1912), 22–27.
[2] Dickson, L. E.: History of the Theory of Numbers, Chelsea, New York, 1952.
[3] Erdõs Pál: On the Converse of Fermat's Theorem, Amer. Math. Monthly, 56(1949), 623–624.
[4] Jeans, J. H.: The Converse of Fermat's Theorem, Messenger Math., 27(1897–1898), 174.
[5] Kiss Elemér: Fermat's Theorem in János Bolyai's Manuscripts, Mathematica Pannonica, 6(1995), nr. 2, 237–242.
[6] Kiss Elemér: Foglalkozott-e számelmélettel Bolyai János?, Természet Világa, 127(1996), 8. szám, 344–348.
[7] Kiss Elemér: Kérdések Bolyai János kutatásairól, Természet Világa, 127(1996), 11. szám, 522–523.
[8] Kiss Elemér: Bolyai János vizsgálatai a 4m+1 alakú prímszámok két négyzet összegére való felbontásáról, Polygon, Szeged, 6(1996), 2. szám, 1–11.
[9] Lehmer, D. H.: Tests for primality by the converse of Fermat's Theorem, Bull. Amer. Math. Soc., 33(1927), 327–340.
[10] Lehmer, D. H.: On the Converse of Fermat's Theorem, Amer. Math. Monthy, 43(1936), 347–354.
[11] Szénássy Barna: Kérdések és válaszok, Bolyai Jánosra emlékezünk! Születésének 175. évfordulóján, Tudományos Ismeretterjesztõ Társulat Budapesti Szervezete, 1978, Szerkesztette Staar Gyula, 29–40.
[12] Vekerdi László: A Bolyai-kutatás változásai, Természet Világa, 112(1981), 2. szám, 56–58.
| Természet Világa, | 1998. III. különszám, 16–20. oldal
http://www.kfki.hu/chemonet/TermVil/ http://www.ch.bme.hu/chemonet/TermVil/ |