A szakmai körök és a nagyközönség részéről komoly érdeklődés figyelhető meg a – modern tudomány szóhasználata szerint – káosznak nevezett jelenség és szokatlan tulajdonságai iránt. A téma az ismeretterjesztő irodalomban hozzáférhető, ugyanakkor általános értelmezése nem mentes néhány tipikus félreértéstől. A káosz jelentőségének és gyakoriságának értékelése az 1980-as évek óta [1] még a területen dolgozók szemében is változott. Cikkünk célja ennek az ezredfordulóra letisztult értelmezésnek a bemutatása, melyhez az is szorosan hozzátartozik, hogy milyen jelenségek nem kaotikusak, mert esetleg még a káosznál is bonyolultabbak. Ennek kapcsán áttekintünk néhány olyan – gyakran előforduló – kijelentést, felvetődő gondolatot, mely a fenti értelmezés szerint tévesnek bizonyul. (Folyóiratunk most közreadott két cikkével útjára indítjuk a káosz rejtelmeit sok irányból bemutató, szemléletgazdagító sorozatunkat, melyet 8-10 részesre tervezünk – a szerk.)
 
 

Meghatározásunk szerint a káosz mozgás, általánosabb értelemben időfejlődés, méghozzá annak is egy bonyolult, összetett formája. A vizsgált rendszerek rendelkeznek mozgásegyenletekkel, azaz mozgásuk jól definiált matematikai struktúrákkal kapcsolatos. A rendszer egyszerűsége azt jelenti, hogy mindössze néhány (mondjuk legfeljebb 10) változó jellemzi állapotát, mozgása ezért néhány egyenlettel egyértelműen leírható. Ezek az egyenletek közönséges differenciál- vagy differenciaegyenletek. E meghatározás kifejezi a meglepő tapasztalati tényt:

A káosz felfedezése és széles körű elfogadása azért váratott magára a XX. század utolsó harmadáig, mert ezek a bonyolult megoldások általában nem adhatók meg képletekkel, csupán számítógépes szimulálásban tárulnak elénk.

Tisztáznunk kell, mit is jelent a bonyolultság. Ez nem definíció, hanem sok ilyen rendszer vizsgálatából leszűrt tapasztalat. Mielőtt ezeket a tapasztalatokat összegeznénk, bemutatunk egy mindenki által könynyen elképzelhető és meg is építhető mechanikai rendszert, mely általában kaotikus mozgást mutat.

Tekintsünk egy időben szinuszosan fel-le mozgó vízszintes lapon – például rezgő hangszórólemezen – függőlegesen pattogó, kisméretű golyót. A lemez rezgése periodikus, a lemezzel való ütközés azonban nem feltétlenül az. A kaotikus viselkedést az okozza, hogy a golyó repülési ideje általában nem azonos a lemez rezgésidejével, így az ütközések mindig különböző fázisokban következnek be. Érdemes a golyó állapotát az ütközések pillanatában, közvetlenül a viszszapattanás után meghatározni. Az ütközési sebességveszteség általában nem hanyagolható el, ezért feltesszük, hogy a golyó lemezhez viszonyított sebességének nagysága a visszapattanás után a becsapódási érték k-szorosa (k<1). Mivel az ütközések közötti mozgás függőleges hajítás, a mechanika törvényei alapján egyértelműen meghatározható a következő ütközés pillanata, valamint az ütközési veszteség ismeretében az ütközés utáni visszapattanási sebesség is. Ha a közegellenállást elhanyagoljuk, akkor ehhez középiskolai ismeretek is elegendőek. A mozgást a visszapattanási sebességek és az ütközési időpontok sorozatának megadásával követjük nyomon. Jellegzetes vonásai az 1. ábráról olvashatóak le.

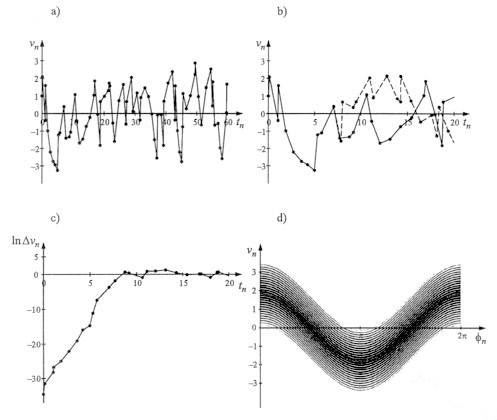
1. ábra. a) Az f frekvenciával rezgő lemezen pattogó golyó t_n ütközési időpillanata és v_n visszapattanási sebessége az ütközések n számának függvényében (t₀=0, v₀=1 m/s). A mozgás szabálytalan, benne semmilyen ismétlődés sem ismerhető fel. b) Két közel  azonos kezdősebességgel indított golyó (t₀=0, v₀=1 m/s, ill. v₀=1+10^–15 m/s, szaggatott vonal) visszapattanási sebességeinek sorozata. c) A sebességkülönbségek logaritmusa lineárisan változik időben, a l= 4 hertz meredekséggel. A sebességkülönbség exponenciálisan nő az exp(lt_n) ütemben. A l kitevő a Ljapunov-exponens, a káosz egyik fontos mérőszáma. A b), c) képekről a  kezdőfeltételre vonatkozó nagyfokú  érzékenység következik.  d) Az idő helyett célszerű az ütközési pillanatok j_n=2pft_n fázisát is követni, ami – mivel szög –  mindig "visszatolandó" a (0, 2p) intervallumba. A j_n,v_n koordinátákkal megadott "pattogási térképen" (ami az ún. fázistérbeli ábrázolás egy esete) az a) ábra pontsorozata 1millió pattanás után egy bonyolult, de strukturált fraktálszerkezettel rendelkező alakzatot rajzol ki, az ún. kaotikus attraktort.

Példánkban f =20 Hz, a lemez maximális sebessége V=1,2 m/s, az ütközési együttható k=0,5. A mozgás egyszerű modelljét használtuk, mely szerint a lemez kitérése elhanyagolható a golyó emelkedéséhez képest, s ezért t_n+1=t_n+(2/g)v_n. Mivel a relatív sebesseég a visszapattanáskor a (–k)-szorosára változik, az új fázis sebessége

(g a gravitációs gyorsulás). Ez egy kétváltozós leképezés (differenciaegyenlet). A kaotikus viselkedés csak nemlineáris rendszerekben fordul elő, esetünkben a nemlinearitás forrása a lemez koszinusz- (azaz a lineáristól eltérő) függvénnyel jellemzett sebessége.
 

Példánk és számos egyéb jelenség vizsgálata [2–4] alapján összefoglalásként elmondhatjuk, hogy a kaotikus mozgás fő tulajdonsága

• az időben szabálytalan, aperiodikus viselkedés, ami nem áll elő tetszőleges számú periodikus mozgás összegeként sem,

• az előrejelezhetetlenség, annak következményeként, hogy a mozgás érzékeny a kezdőfeltételekre, melyeket azonban sohasem ismerünk teljesen pontosan,

• a fázistérbeli bonyolult, de rendezett fraktálszerkezet [5], melynek fraktáldimenziója kis (10-nél mindenképpen kisebb) szám.

Hangsúlyozzuk azonban, hogy (a definíció értelmében, mely szerint a káosz a kevés öszszetevőből álló rendszerek időben bonyolult megnyilvánulása) egy jelenséget csak akkor tekinthetünk kaotikusnak, ha sikerül olyan egyszerű modellt is találni, mely a szabálytalan viselkedést kellő pontossággal visszaadja.

A káosz számos hétköznapi folyamat (pl. a flipper golyójának mozgása, a rádió begerjedése, festékek keveredése) mellett szerepel műszaki jelenségekben (pl. a kerekek és szerszámgépelemek mozgásában, a vontatott pótkocsik kilengésében), a szennyezések szétterjedésének dinamikájában, biológiai jelenségekben (pl. járványok lefolyásában) és jóval nagyobb léptékben például a Naprendszer egyes alkotóelemeinek mozgásában.
 
 

A káosz nem térbeli, statikus rendezetlenség, annak ellenére sem, hogy a hétköznapi szóhasználatban káoszon gyakran éppen térbeli összevisszaságot értünk.

A káosz nem hagyományos, szabályos mozgás. Az utóbbi minden fő vonásában különbözik a káosztól: ismétlődő, azaz periodikus (vagy majdnem periodikus), előre jelezhető, nem kapcsolatos fraktálstruktúrákkal és nem is véletlenszerű.

A káosz nem zaj. A zajos mozgás a nagyon sok összetevőből álló rendszerek valamely komponensének véletlenszerű viselkedése (pl. egy részecske Brown-mozgása), mely a környezettel (a többi összetevővel) való bonyolult kölcsönhatás következménye.

A káoszt a szabályos mozgástól az különbözteti meg, hogy véletlenszerű, a zajostól pedig az, hogy véletlenszerűsége a kevés összetevőelem erős (de egyszerű törvényt követő) kölcsönhatásából, a belső dinamikából adódik. A zajos mozgások a fázisteret egyenletesen töltik ki, bennük fraktálstruktúrák nem alakulhatnak ki. A valószínűségi leírás szempontjából a káosz és a zaj sok vonásában egyenértékű, csupán a véletlen viselkedés eredete különböző.

A káosz nem egyszeri instabilitás. Egy állapot akkor instabil, ha a rendszert onnét kissé kitérítve távolodni kezd az eredeti állapottól. Az instabil állapot körüli kis eltérések drasztikusan különböző végkifejletre vezetnek. Erre példa a feldobott pénzdarab mozgása (az élére is eshet!), melynek végeredményét mindig is véletlen folyamatnak tekintették. Az instabilitás tehát eleve előrejelezhetetlenséggel, véletlenszerű viselkedéssel jár együtt, önmagában azonban nem jelent kaotikusságot. Az élére esett pénzdarab mozgása a feldőlés megkezdése után nem instabil többé, s ezért nem is tekinthető kaotikusnak. Az instabilitás csak szükséges feltétele a káosznak. Az elégséges feltétel az, hogy ez az instabilitás a mozgás során tetszőlegesen hosszú ideig fennálljon, újra és újra felbukkanjon.
 

Kaotikus viselkedés csak akkor lehetséges, ha a mozgás mindig újabb és újabb instabil állapotok közelébe kerül.

A káosz nem a sok összetevőjű, nagy szabadsági fokú rendszerek időbeli viselkedése. Az ilyen időbeli viselkedés szükségszerűen bonyolultabb a káosznál. Az 1. ábrán bemutatott rendszer általánosításaként gondoljunk például egy sok kicsi golyóból álló, vékony fonállal összekötött láncra. Ez a rezgő lemezen nemcsak időben aperiodikusan mozog, hanem közben egyre változó alakokat is felvesz. Minden térbeli és időbeli folyamatban (pl. kémiai reakciók, ingerületvezetés) nem túl nagy energiabefektetés esetén előfordulhat, hogy a mozgásban a szabadsági fokok bizonyos csoportjai vesznek csak részt. A megfigyelő számára ez azt jelenti, hogy többé-kevésbé szabályos térbeli mintázatok (pl. hullámok) vonulnak át a rendszeren, de ezek ismétlődése időben sohasem pontosan periodikus. Az ilyen térbeli és időbeli káosz tehát első közelítésben bizonyos térbeli struktúrák előfordulási gyakoriságában mutatkozik meg. A jellemző térbeli struktúra megjelenése számos új jelenséggel (nemlineáris hullámokkal, csúcsokkal, frontokkal, peremektől függéssel, határréteggel, koherens, illetve szinkronizált viselkedéssel) kapcsolatos. A kaotikus mozgás ismerete csak első lépés a térbeli és időbeli káosz megértése felé, melyhez bizonyára hosszú évek további kutatásai után juthatunk csak el.

A káosz nem turbulencia. A turbulencia a folyadék (vagy más folytonos közeg) mozgásának legbonyolultabb formája, mely időben is és térben is teljesen szabálytalan (a nagy szabadsági fokú viselkedés extrém esete). A káosztudomány kialakulása idején, az 1970-es és 1980-as években széleskörűen elfogadott volt, hogy a káosz megértése a turbulencia megértését is jelenti majd. Mára világossá vált, hogy ez túlzott várakozásnak bizonyult.
 
 

jó, ha tudjuk:

Nem igaz, hogy bármilyen kaotikus modell leírhat valóságos kaotikus folyamatot. A valóságos mozgások leírására differenciálegyenleteket használunk. Léteznek olyan matematikai modellek, például differenciaegyenletek, melyek nem kapcsolatosak differenciálegyenletekkel, és ezért nem is írhatnak le valóságos mozgásokat. Az ilyen modellek időfejlődése, absztrakt értelemben vett mozgása a definíciónk értelmében lehet kaotikus. Példa erre a másodfokú komplex leképezések esete, melyekhez a híres Mandelbrot-halmaz is tartozik [6]. A matematika apparátusa (a dinamikai rendszerek elmélete) tehát többfajta káoszt is megenged, mint a fizika vagy más tudományok, melyekben a mozgás differenciálegyenletekhez kötött.

A káosz nem univerzális. A rendszer részleteitől független, univerzális viselkedés csakis a káosz kialakulása során, ott is csak bizonyos forgatókönyvek esetében (pl. az ún. Feigenbaum-féle perióduskettőző bifurkációsorozat torlódási pontja körül) érvényes. A káosz univerzális vonásainak alkalmazási lehetőségei jóval kisebb súlyúnak bizonyultak, mint ahogy az 1980-as években várták.

Tévedés, hogy a káosz tudománya szerint minden mindennel összefügg. A kaotikus viselkedés, például a kaotikus attraktoron való mozgás valóban nem bontható részeire. Ebből azonban nem következik, hogy különböző kaotikus rendszerek között kölcsönhatásnak kellene fennállnia.

A légkör nem kaotikus. A légkör sok öszszetevőből álló, nagy szabadsági fokú rendszer, melynek állapota gyakran turbulens. A meteorológia ennek ellenére fontos szerepet játszott és játszik a káosz kutatásában. Edward Lorenz meteorológus fedezte fel 1963-ban, hogy az egyszerű rendszerek is lehetnek előrejelezhetetlenek. A legújabb kutatások azt bizonyítják, hogy bizonyos földrajzi helyeken és bizonyos időpontokban a légkör úgy viselkedhet, mint egy kevés öszszetevőből álló rendszer. Ott és ilyenkor ezért a káoszról szerzett ismeretek haszonnal alkalmazhatóak.

Nem igaz, hogy a pillangóeffektus szerint a világ kiismerhetetlen.Edward Lorenz 1972-ben előadást tartott a következő címmel: „Előrejelezhetőség: Okozhat-e tornádót Texasban egy brazíliai pillangó szárnycsapása?”. A pillangóeffektus elnevezés Gleick könyvének szóhasználata alapján terjedt el, ráadásul abban az értelemben, hogy a kérdésre pozitív a válasz. A szakirodalmon kívül ezt gyakran úgy értelmezik, hogy a modern természettudomány szerint semmiben sem lehetünk biztosak. Ezzel szemben a kaotikus rendszerek vizsgálata azt mutatja, hogy az előrejelezhetetlenség korlátozott, csakis a kaotikus attraktoron áll fenn. Az attraktor elérését megelőző mozgásról biztosan tudjuk, hogy egy nagyon kicsi, nulla térfogatú (de kiterjedt) halmaz – az attraktor – felé tart a fázistérben. Ráadásul az attraktoron kialakuló mozgás statisztikai szempontból teljesen pontosan megismerhető. A Lorenz-előadásban feltett kérdésre tehát csak akkor adható meg a válasz, ha el tudjuk dönteni, hogy a Brazíliából induló eredeti és a szárnycsapással odébbpöckölt mozgáspálya rajta van-e azon az attraktoron, amelyhez a texasi tornádó tartozik. Erre már csak azért is kevés az esély, mert a déli és az északi félteke légtömegei között gyakorlatilag nincs kölcsönhatás. A történeti teljességhez hozzátartozik, hogy előadásában Lorenz azt is megjegyezte [7], hogy ha egy pillangószárnycsapás kiválthat tornádót, akkor meg is akadályozhatja azt. A szélsőséges események statisztikai gyakorisága tehát nem nő a pillangó miatt; a hasonlat csupán a jelenség véletlenszerű viselkedését illusztrálja. Mindezzel Lorenz az időjárás-előrejelzési nehézségekre utalt, és a címben feltett kérdésre végül is nem adott választ. Az újságíró Gleick mindezt nem említi könyvében.

Ha valami előrejelezhetetlen, abból nem következik, hogy kaotikus. A Ljapunov-exponens (1.c ábra) pozitív értéke a kezdőfeltételre mutatott érzékenységre és így az előrejelezhetetlenségre utal. Ebből azonban nem következik az alacsony dimenziós fraktálviselkedés, ami a káosz egy másik lényeges tulajdonsága. Ha tehát valami hosszú távon előrejelezhetetlen, akkor az legalább olyan bonyolult, mint a káosz, de lehet annál bonyolultabb, például térbeli és időbeli káosz vagy turbulenciaszerű jelenség is.

Egy természeti vagy társadalmi jelenséggel kapcsolatos idősor általában nem kaotikus.A káosz alkalmazásának egyik fontos lehetősége lenne, ha egy megfigyelt idősorról (egyetlen változó időfüggéséről) ki lehetne mutatni, hogy az kaotikus folyamathoz tartozik, anélkül hogy a mozgásegyenleteket ismernénk. Létezik egy algoritmus annak eldöntésére, hogy egy hosszú idősor milyen fraktáldimenziójú attraktorral kapcsolatos. Ezt az 1980-as és 1990-es években széleskörűen alkalmazták például a meteorológiai hőmérséklet, a napfoltok intenzitása, az agyi elektromos tevékenység (EEG-jelek) vagy gazdasági adatok idősorainak elemzésére, annak ellenére, hogy ezt sokan már akkor is szkeptikusan fogadták. Eleinte szinte mindegyikben alacsony (3 és 4 közötti) dimenziók adódtak (s ennek megfelelően beszéltek pl. időjárási attraktorról stb.), de az eljárások finomodásával – a feldolgozott adatok hosszának növekedésével – ezek az értékek egyre nagyobbá váltak. Az eljárás a tapasztalat szerint nem konvergál.

Az idősor-analízis mai alkalmazási iránya ezért már nem a kaotikusság bizonyítása, hanem annak kiderítése, hogy a jelnek van-e egyáltalán determinisztikus komponense, vagy teljes egészében zajnak tekintendő-e [8].

A társadalmi jelenségek definíciónk szerint nem kaotikusak. A társadalom biztosan nem egyszerű rendszer, s időfejlődése ezért definíciónk értelmében nem is lehet kaotikus. Ez természetesen nincs ellentmondásban azzal, hogy a társadalmi jelenségek a tapasztalat szerint előrejelezhetetlenek, de arról sem szabad megfeledkeznünk, hogy egyelőre nem is ismeretesek azok a törvények és a törvényeket kifejező matematikai egyenletek, melyek segítségével az egész társadalom leírható lenne. Ezért véleményünk szerint mai tudásunk nem elegendő ahhoz, hogy a társadalom egészének kaotikusságát tudományos értelemben jól definiált kérdésnek tekinthessük.
 
 

A káosz tehát egy érdekes, a hagyományoshoz képest újfajta mozgásforma. Létezésének vannak az emberi felhasználás szempontjából hasznos és hátrányos következményei is. Hasznos például a tésztagyúrás folyamatában, melynek során az egyes anyagok (só, vaj stb.) részecskéi kaotikusan mozognak, s éppen ez vezet a jó keveredéshez. A turmixgép is annál hatékonyabb, minél kaotikusabb benne a folyadékelemek mozgása. Az áramkörök kaotikus működése használható titkosított üzenetek továbbítására és szinkronizálásra is. A szabálytalan rezgések kialakulása, az áramkörök begerjedése vagy az űrhajók eltérülése a tervezett iránytól viszont olyan folyamatok, melyeket elkerülni igyekszünk. A káosz egyik különleges tulajdonsága, hogy időbeli szabálytalansága ellenére jól kontrollálható, szabályozható. Az egyik legelterjedtebb eljárás a bölcs gyermeknevelésre emlékezet: megvárjuk, amíg a rendszer a kaotikus mozgás során magától olyan állapotba jut, ahol jól megválasztott kis külső hatás is elegendő ahhoz, hogy következményeként a mozgás periodikussá, tehát szabályossá váljék, azaz a kaotikusság ne maradjon fenn többé.

Az eddigiekből nyilvánvaló, hogy a kaotikus rendszerek mozgása bonyolult, de megérthető: meglepetésekkel szolgál és vizsgálóját a felfedezés örömével ajándékozza meg. Ugyanakkor a káosz a komplex viselkedésnek távolról sem a legmagasabb szintje. Cikksorozatunk célja a káosz széles körű alkalmazási területeinek és az ezeken elért új eredményeknek a bemutatása.

Köszönettel tartozunk Jánosi Imre, Muraközy Gyula, Scheuring István, Stépán Gábor és Vattay Gábor kollégáinknak hasznos megjegyzéseikért.
 

IRODALOM

1. J. Gleick, Káosz, egy új tudomány születése (Göncöl Kiadó, Budapest, 1999), az Amerikai Egyesült Államokban 1988-ban jelent meg először
2. A káosz és rendezetlenség vizsgálata, Magyar Tudomány (különszám), vendégszerkesztő: Szépfalusy Péter, 1993
3. E. Ott, Chaos in Dynamical Systems (Cambridge University Press, 1993)
4. Tél T., Gruiz M., Kaotikus dinamika (Nemzeti Tankönyvkiadó, Budapest, 2002)
5. Tél T., Természet Világa, 115. évf. 106. old. 1984
6. Kecskés L., Természet Világa, 135. évf., 267. o., 2002. június
7. E. N. Lorenz, The Essence of Chaos (The University of Washington Press, 1993)
8. H. Kantz, Th. Schreiber, Nonlinear Time Series Analysis (Cambridge University Press, 1999)