
melyen megfigyelhetô (balról jobbra)
egy RHHRHHR sorozat
MATEMATIKA
MARTIN GARDNER
Penrose csempéi
Második rész
Az elmúlt évtizedben, mióta a Penrose-csempézésrõl szóló cikkem megjelent a Scientific Americanben (1977. január), Roger Penrose, John Conway, Robert Ammann és mások hatalmas lépéseket tettek a nem periodikus csempézések felderítése terén. (Változatlanul a "nem periodikus" kifejezést fogom használni, bár Branko Grünbaum és G. C. Shephard a Tilings and Patterns címû nagyszabású mûvükben "aperiodikus"-nak hívnak egy csempekészletet, ha azzal csak nem periodikusan csempézhetõ a sík. Annak felfedezése, amit manapság Ammann-csíkoknak vagy egyeneseknek nevezünk, és a Penrose-csempézés háromdimenziós megfelelôi, a kristálytan bámulatos fejlôdéséhez vezetett, de elõször is hadd foglaljam össze ennek az áttörésnek az elôzményeit.
 |
| 1. ábra. Az Ammann-csíkok egy családja, melyen megfigyelhetô (balról jobbra) egy RHHRHHR sorozat |
Egy tehetséges fiatal matematikus, Robert Ammann, aki alacsony szintû számítógépes munkákat végzett Massachusettsben, Penrose-tól függetlenül felfedezte a rombusz-csempéket 1976-ban, körülbelül nyolc hónappal a Penrose-csempézésrõl szóló cikkem megjelenése elôtt. Levélben számoltam be neki a dárdákról és sárkányokról, melyben azt is megírtam, hogy Penrose már korábban felfedezte a rombuszokat. Ammann hamarosan rájött, hogy mindkét csempepár olyan mintákhoz vezet, melyeket öt, párhuzamos egyenesekbôl álló egyenescsalád határoz meg, ahol az egyenesek öt különbözõ irányban haladnak át a síkon, 360/5=72 fokos szögben metszve egymást. Egy ilyen egyenescsalád mai elnevezéssel Ammann-csíkok látható az 1. ábrán.
Észrevehetô, hogy az egyenesek olyan dárdák konkáv csúcsán haladnak át, melyek egyik része egy irányba, a többi pedig ellenkezô irányba mutat. Szigorú értelemben ez nem pontos meghatározás az egyenesek elhelyezkedésére, de a mi céljainknak ez az egyszerû szabály is megfelel. A precíz meghatározás a GrünbaumShephard-könyvben megtalálható. Ha a pontos helyükre kerülnek az egyenesek, akkor mindegyik egy hajszálnyival a dárdák konkáv csúcsán kívül halad. A minta minden szabályos tízszögének belsejében tökéletes pentagrammát (ötágú csillagot) rajzolnak ki az Ammann-csíkok.
A szomszédos egyenesek között kétféle távolság figyelhetõ meg, az egyiket H-val (hosszabb), a másikat R-rel (rövidebb) fogjuk jelölni. Ha megfelelôen helyezzük el az egyeneseket, akkor a két távolság aranymetszéssel aránylik egymáshoz. Ráadásul a teljes síkot tekintve az egy családon belül levô csíkok között a H-k számának aránya a R-ek számához szintén aranymetszés. Ha elindulunk a csíkok egyik családjára merôleges irányban, H-k és R-ek sorozatával jegyezhetjük le az egymást követô távolságokat. Ez a sorozat nem lesz periodikus, és a Penrose-csempézésnek szép, egydimenziós megfelelõjét adja, teljesül rá a lokális izomorfizmus-tétel. Bármilyen véges részét kiválasztva a sorozatnak, mindig meg fogjuk találni a közelben annak másolatát. Induljunk el bárhol és jegyezzünk fel akárhány betût véges sok, mondjuk egymilliárd lépésen keresztül. A sorozat bármelyik pontjáról elindulva biztosak lehetünk abban, hogy elérünk egy ugyanilyen egymilliárd betûs sorozatot. Csak akkor nem ismétlõdik meg a betûsorozat, ha végtelen.
Conway felfedezte, hogy ez a sorozat a következôképpen kapható meg az aranymetszésbõl. Írjuk fel növekvô sorrendben az aranymetszés arányszámának ((1+51/2)/2) a többszöröseit, lefelé kerekítve a legközelebbi egész számra. A kapott sorozat így fog kezdôdni: 1, 3, 4, 6, 8, 9, 11, 12, 14, 16, 17, 19, 21, 22, 24, 25, 27, 29, 30, 32, 33, 35, 37, 38, 40, 42, 43, 45, 46, 48, 50, ... Ez a 917-es számú sorozat N. J. A. Sloane: Handbook of Integer Sequences (Egész számokból álló sorozatok kézikönyve) címû könyvében. Ha az aranymetszés négyzetének a többszöröseit kerekítjük le, akkor a 2, 5, 7, 10, 13, 15, 18, 20, 23, ... sorozatot kapjuk. A két sorozatot szokás egymás "komplementerének" nevezni. A kettõ egyesítésében minden pozitív egész egyszer és csak egyszer fordul elô. Ha egy tetszõleges a valós szám többszöröseit kerekítjük lefelé a legközelebbi egészre, akkor az így kapott sorozatot az a spektrumának nevezik. Ha a irracionális, akkor szokás a sorozatot Beatty-sorozatnak hívni, Samuel Beatty kanadai matematikus neve után, aki az ilyesfajta sorozatokra irányította a figyelmet 1926-ban. Mint arról egy másik cikkemben írtam, az aranymetszésen alapuló komplementer Beatty-sorozatok szolgáltatják a NIM-játék Wythoff-játéknak nevezett híres változatának nyerô stratégiáját.
Az aranymetszéses Beatty-sorozat szomszédos tagjainak különbsége vagy 1, vagy 2. Ha felírjuk az elsô különbségsorozatot, majd minden 1-est 0-ra és minden 2-est 1-re változtatunk, egy végtelen bináris sorozatot kapunk, amely így kezdôdik: 101101011011010... Ez az Ammann-csíkok bármelyik végtelen családjában az R-ek és H-k sorozatának egy darabja. Conway a "zenei sorozat" kifejezést használja az aranymetszéses sorozat bármelyik véges szakaszára. Én Penrose-t követve Fibonacci-sorozatoknak fogom ôket ne vezni. [Az elnevezés némileg félreérthetõ, ugyanis általában az 1, 1, 2, 3, 5, 8, 13, 21, ... (minden további tag az elõzõ összege) sorozatot szokás Fibonacci-sorozatnak nevezni, vagy néha ennek azt az általánosítását, ahol az elsõ két tag tetszõleges, a képzési szabály viszont ugyanaz. (A fordító)]
Az ilyen sorozatok számos érdekes tulajdonsággal rendelkeznek, ha például a fenti, binárisan megadott Fibonacci-sorozat elé tizedesvesszôt rakunk, akkor az eredmény egy olyan irracionális szám kettes számrendszerbeli vesszôstört alakja lesz, melyet a következô lánctört határoz meg:

A lánctörtben szereplô kitevõk éppen a Fibonacci-számok. Conway számos publikálatlan eredménnyel rendelkezik arról, hogy a Penrose-csempézések hogyan függenek össze a Fibonacci-számokkal, amik viszont különbözô növények növekedési szabályaival függenek össze.
A Penrose-csempézések, mint láttuk, ön-hasonlóak abban az értelemben, hogy ha felfújjuk vagy leeresztjük ôket, akkor egy másik csempézést kapunk. A Fibonacci-sorozatok is rendelkeznek ugyanevvel a tulajdonsággal. Sokféle módon felfújhatók és leereszthetôk úgy, hogy egy másik ilyen sorozatot kapjunk, de a legegyszerûbb a következô. A leeresztéshez cseréljünk ki minden R-et H-ra, minden HH-t R-re, és hagyjuk el az egyedül álló H-kat. Ha például a HRHHRHRHHRHHRHR sorozatot ezzel a szabállyal eresztjük le, akkor a leeresztettje HRHHRHRHH. A felfújáshoz cseréljünk ki minden H-t R re, minden R-t HH-ra, és két R közé mindenhova rakjunk be egy H-t.
Egy Fibonacci-sorozatban sosem fordulhat elõ RR vagy HHH. Ezt felhasználva könnyen eldönthetõ, hogy R-ek és H-k egy sorozata Fibonacci-e. Alkalmazzuk a leeresztési szabályt egészen addig, míg vagy egy olyan sorozatot nem kapunk, amelyben RR vagy HHH van (ebben az esetben a sorozat nem Fibonacci), vagy egyetlen betût nem kapunk, ami bizonyítja, hogy az. Egy Penrose-csempézés felfújásakor vagy leeresztésekor az Ammann-csíkok bármelyik családjához tartozó sorozat is felfújódik, illetve leeresztôdik. Bármelyik olyan hernyóban, mint a kocsikerékminta tíz küllôjének hernyói, a hosszú és rövid csokornyakkendôk sorozata szintén Fibonacci-sorozat.
Az Ammann-csíkok két családja nem periodikus paralelogrammák olyan hálózatát hozza létre, melybe beleilleszkednek a csempék. Ahogy Grünbaum és Shephard fogalmazza, "az, ami alapvetô, az a csíkok rendszere, és a csempék szerepe mindössze az, hogy egy gyakorlati megvalósítást adnak". A csíkok valami olyasmik, amik halványan emlékeztetnek a kvantummezôkre, melyek meghatározzák a részecskék helyét és pályáját. Ammann volt az elsô, aki már 1977 elején észrevette, hogy a csíkok hálózata "kényszertételek"-hez vezet olyan tételekhez, melyek arról szólnak, hogy csempék egy kicsiny halmaza hogyan határozza meg végtelen sok más csempe helyzetét.
Ammann ezt így fogalmazta meg egy nekem írt levélben: "Valahányszor csempék egy halmaza egy bizonyos helyzetbe kényszerít egy párhuzamos egye3nest, akkor ezzel végtelen sok nem szomszédos párhuzamos egyenest is bizonyos helyzetbe kényszerít. Valahányszor három egyenes megfelelô szögben metszi egymást, ez kikényszerít egy csempét". Ez a tulajdonság, hogy csempék egy véges halmaza kikényszeríti tetszõlegesen nagy távolságra levô csempék helyzetét, a Penrose-rombuszok mellett a Robinson-négyzetekre is jellemzô, pedig ezek semmilyen kapcsolatban nincsenek az aranymetszéssel.
Ammann felfedezéseibõl kiindulva Conway számos további figyelemre méltó kényszertételt mondott ki. Most csak azt említem meg, miszerint két Penrose-csempe (mindkettô akármilyen típusú lehet), ha megfelelôen helyezzük el ôket, tetszôleges távolságra egymástól, csíkok két végtelen (nem teljes) családját határozza meg. Az egymást metszô két egyenescsalád viszont végtelen sok csempe helyzetét határozza meg. A király, dáma, bubi, kettes és a csillag például olyanok, hogy birodalmukban végtelen sok csempe helyét kényszerítik ki. (Az ász és a nap nem kényszerít ki egyetlen csempét sem.) A király birodalma különösen sûrû. Azt hihetnénk, hogy a kikényszerített csempék sûrûsége csökken, ahogy távolodunk a centrumtól, de nem ez a helyzet. A sûrûség a teljes síkon állandó.
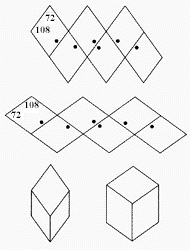 |
| 2. ábra. A tompa- és a hegyesszögû arany romboéder testhálója |
Ammann másik nagy felfedezése, szintén 1976-ból, egy két romboéderbôl (olyan paralelepipedon, melynek hat egy bevágó rombuszlapja van) álló készlet volt, mellyel alkalmas illesztési szabályok esetén csaknem periodikusan csempézhetô a tér. A két romboéder testhálója a 2. ábrán látható. Ha kartonpapírból kivágjuk a két hálót, a vonalak mentén összehajtva és az éleket összeragasztva megkapjuk az ábra alsó részén látható két testet. Az egyik olyan, mint egy testátlója mentén összenyomott, a másik pedig, mint egy testátlója mentén széthúzott kocka. Mind a tizenkét lap egybevágó, a lapátlók aránya aranymetszés. H. S. M. Coxeter, a híres geométer, az ilyen típusú romboédereket "arany romboéder"-nek nevezte W. Rouse Ball klasszikus Mathematical Recreations and Essays (Dover, 1987.) címû mûvének, melyet ô szerkesztett, a tizenharmadik kiadásában, egy, a 161. oldalhoz fûzött jegyzetében. Mindössze kétféle arany romboéder van, melyek mindegyikét tanulmányozta már Kepler is. A hegyes szögû arany romboédernek van két átellenes csúcsa, melyben három egyenlô hegyesszög találkozik. A tompaszögû arany romboédernek olyan két átellenes csúcsa van, melyben egyenlô tompaszögek találkoznak. Mindkét test több csúcsában vegyesen fordulnak elô hegyes- és tompaszögek.
Ammann két romboédere éppen a kéféle arany típusú. A periodikus csempézést megfelelôen elhelyezett lyukakkal és kiemelkedésekkel akadályozhatjuk meg. Figyeljük meg az ábra testhálóin a pöttyöket. Képzeljük el, hogy mindkét testnek elkészítjük a másolatát úgy, hogy a pöttyök mintázata a tükörképe legyen az eredetiének. Ekkor egy olyan, négy testbôl álló készletet kapunk, mellyel csaknem periodikusan lehet csempézni, ha úgy illesztjük össze a darabokat, hogy minden pötty fedjen egy másik pöttyöt. Nem tudni, hogy ez a tükrözés kihagyható-e úgy, hogy csak két megfelelô jelölésekkel ellátott test kényszerítse ki a nem periodikus csempézést. Ha egy sík megfelelô szögben metszi a kicsempézett teret, akkor a síkon a Penrose-rombuszokéhoz nagyon hasonló csempézés jelenik meg.
Elküldtem Ammann eredményeit Penrose-nak. Egy 1976. május 4-re datált levélben Penrose megkért, hogy továbbítsam gratulációit Ammann-nak két dologért is: a rombuszcsempék független felfedezéséért és a tér csempézéséért a két arany romboéderrel. Így folytatta:
Még az is lehetséges, hogy ezek a dolgok jelentôséggel bírhatnak a biológia szempontjából. Ne felejtsük el, hogy bizonyos vírusok szabályos dodekaéder és ikozaéder alakban növekednek. Mindig is zavarba ejtô kérdés volt, hogy hogyan csinálják ezt. Ammann nem periodikus testjeivel viszont mint alapegységekkel, kváziperiodikus "kristályokhoz" juthatunk, olyan látszólag lehetetlen (kristálytanilag) hasadási irányokkal, melyek síkjai dodekaédert vagy ikozaédert határoznak meg. Lehetséges, hogy talán a vírusok növekedése is valami ilyesfajta nem periodikus egységen alapul - vagy túlságosan elrugaszkodott ez az elképzelés?
Egy évvel a tér Ammann-féle nem periodikus csempézésének felfedezése után a japán Koji Miyazaki, a kobei egyetem építésze újra felfedezte azt. Ezenkívül talált egy másik módot is arra, hogy a két arany romboéderrel nem periodikusan csempézzük a teret, bár ez a csempézés nem kikényszerített. Öt hegyesszögû és öt tompaszögû arany romboéder illeszkedik úgy össze, hogy egy rombikus triakontraédert alkotnak. Két ityen testet, melyek hegyesszögû csúcsukban érintkeznek, körülvehetünk további hatvan arany romboéderrel (mindkét típusból 30) úgy, hogy egy nagyobb rombikus triakontraédert kapjunk. Ez a nagyítás a végtelenségig folytatható, méhsejtszerûen csempézve a teret, melynek közepe ikozaéderes szimmetriát mutat.
Penrose sejtései a kristályokról még megfogalmazásukat tekintve is meglepôen profetikusnak bizonyultak. Az 1980-as évek elején számos természettudós és matematikus kezdte fontolóra venni annak lehetôségét, hogy kristályok atomi szerkezete esetleg alapulhat egy nem periodikus hálózaton is. Ezt követôen 1984-ben Dany Schechtman és kollégái a Nemzeti Szabványügyi Hivatalnál drámai bejelentéssel álltak elô. Nem periodikus szerkezetet találtak egy hirtelen lehûtött alumínium-mangán ötvözetnek melyet a kémikusok azonnal elneveztek Schechtmanitnak az elektronmikroszkópos vizsgálata során. A mikroszkóp világosan mutatta az ötszöges szimmetriát, ami erôsen sugall egy a Penrose-csempézéssel analóg nem periodikus csempemintát a térben.
Semmi ehhez hasonlót nem tapasztaltak korábban, ahogy Ivars Peterson szakíró megfogalmazta, ez olyan volt, mintha valaki egy ötszögû hópelyhet figyelt volna meg. A krisztallográfiában régóta egyfajta dogmának számított, hogy a kristályok csak 2, 3, 4 vagy 6-szoros forgásszimmetriával rendelkezhetnek, 5, 7 vagy 8-szorossal soha. Egy másik dogma szerint a szilárd anyagok szerkezete csak kétféle lehet, az atomok elrendezése vagy periodikus, vagy teljesen rendezetlen, mint az üveghez hasonló amorf anyagokban.
A rendezett szerkezetû kristályok közül minden ismert kristályhálót három szabályos platóni testre tetraéder, kocka, oktaéder vezettek vissza. A dodekaédert és az ikozaédert azért zárták ki, mert ötszörös szimmetriájuk lehetetlenné tette a periodikus csempézést. És akkor itt volt egy anyag, amely úgy tûnt, hogy ikozaéderes szimmetriát mutat. Akárcsak a Penrose-csempézés 72 fokkal, azaz a teljes kör ötödrészével elforgatva nagyjából egy általános statisztikai értelemben változatlan maradt, de hosszú távú periodicitás nélkül. Úgy tûnt, hogy a szerkezete valahol félúton van az üveg és a rendezett kristályok között, azt mutatva, hogy a kétféle szerkezet közti éles határ helyett átmeneti formák folytonos sokasága lehetséges.
A fizikusok, kémikusok és krisztallográfusok körében ez a felfedezés a robbanás erejével hatott. Hasonló, nem periodikus szerkezeteket fedeztek fel hamarosan más ötvözetekben, és cikkek tucatjai kezdtek megjelenni. Világossá vált, hogy szilárd anyagok nem periodikus rácsszerkezete bármiféle forgásszimmetriát mutathat. Két vagy több csempébôl álló térbeli készletek széles választékát adták meg modellként, melyek némelyike kikényszeríti a nem periodikus csempézést, némelyike pusztán lehetôvé teszi. Elôállítottak egy réteges kristályszerkezetet, melynek egymáson fekvô rétegei a Penrose-féle síkbeli rombuszos csempemintát mutatják. A holland N. G. de Bruijn kifejlesztette a nem periodikus csempézés algebrai elméletét, amely az Ammann-csíkokhoz hasonló, általa "pentarácsok"-nak nevezett szerkezeteken alapul. Egy 1987-es publikálatlan cikkben meglepô kapcsolatról számolt be a nem periodikus csempézések elmélete és egy kártyakeverési tétel melyet a bûvészek Galbreath-féle elv néven ismernek között. (ErrõI az elvrôl a New Mathematical Diversions from Scientific American címû könyvem 9. fejezetében írtam.)
Mindezek igen megtermékenyítôen hatottak a "kvázikristályok" ahogy most ezeket az új, félúton levô kristályokat nevezik kísérleti és elméleti kutatására. Ugyanakkor ellenzôi is vannak annak a nézetnek, hogy ezek a rácsszerkezetek természetükbõl adódóan nem periodikusak. Az ellenzôk vezéralakja Linus Pauling, aki szerint a mikroszkópos képet úgy kellene magyarázni, hogy az ötszörös szimmetria hamis formáját mutatja, melyet a krisztallográfusok sokszoros ikerképzôdésként ismernek. "Nem kell tovább aggódniuk a krisztallográfusoknak amiatt, hogy tudományuk egyik elfogadott alappillérének érvényessége megkérdôjelezôdött" jelentette ki Pauling a Nature egy 1985-ös cikkében. Egy másik lehetôség, hogy a kvázikristályok egyszerûen csak hatalmas egységcellái egy periodikus mintának, ami ki fog derülni, mihelyt nagyobb mintákat készítenek. És vannak más lehetôségek is. A kvázikristályok hívei azt állítják, hogy mindezeket az alternatív magyarázatokat kizárták, és a nem periodikus minta a legegyszerûbb magyarázat. Lehet, hogy néhány éven belül a kísérleti kutatások megcáfolják, és a kvázikristályok a balsorsú polivíz sorsára jutnak; de ha a nem periodikus magyarázat igaznak bizonyul, akkor az szenzációs fordulópont lesz a krisztallográfiában.
Feltéve, hogy a kvázikristályok tényleg léteznek, a következô néhány évben várhatóan egyre hatékonyabb technikák fognak megszületni az elôállításukra. Sok kérdés vár válaszra. Miféle fizikai erôk játszanak szerepet az ilyen furcsa kristályok képzôdésében? Penrose felvetette, hogy talán szerepe van a nem lokális kvantumhatásoknak, hiszen egy átfogó terv nélkül nehezen látható, hogy miképp nôhet egy ilyen kristály oly módon, hogy hosszú távon megôrizze nem periodikus mintázatát. (1976-os levelének abban a részében, ahonnan a vírusokkal kapcsolatos gondolatait idéztük, Penrose azon elmélkedik, hogy egy kvázikristály növekedését hogyan irányíthatják nem lokális erõk.) Milyenek a rugalmassági és elektromos tulajdonságai a kvázikristályoknak? Fognak-e a geológusok valaha is természetes módon képzôdött kvázikristályt találni?
Ha a kvázikristályok olyanok, mint amilyennek hívei hiszik õket, akkor kitûnô példát szolgáltatnak arra, hogy hogyan derülhet ki valamirôl, amit a népszerû matematika pusztán a szórakozás és az esztétikai élvezet kedvéért hozott létre, hogy a fizikai világban és a technológiában jelentôs gyakorlati alkalmazásai vannak.
1980-ban meghallgattam Conway egy elôadását a Penrose-csempézésrõl a Bell Laboratóriumban. A "lyukak elméletének" tárgyalása során elmondta, hogy szeret elképzelni egy hatalmas templomot, melynek a padlója Penrose-csempékkel van kirakva, pontosan középen egy oszloppal. Úgy látszik, mintha a csempézés folytatódna az oszlop alatt. Valójában az oszlop egy csempézhetetlen lyukat fed el. Mellesleg az Ammann-csíkok sora megtörik, amikor keresztülhaladnak a lyukon.
Egy Penrose-féle csempeminta nyilván mindig kiszínezhetô négy színnel úgy, hogy semelyik két közös éllel rendelkezô csempe nem egyforma színû. Vajon kiszínezhetô-e három színnel? A lokális izomorfizmus-tételbôl belátható, mondta Conway, hogy ha bármelyik Penrose-csempeminta kiszínezhetô három színnel, akkor az összes többi is, de mindeddig senki nem bizonyította, hogy bármelyik végtelen minta is kiszínezhetô lenne három színnel.
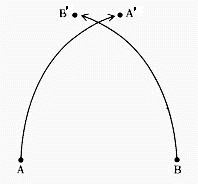
Conway elmondott egy egyszerû indirekt bizonyítást (amit ô Peter Barlow brit matematikusnak tulajdonított, aki 1862-ben halt meg, és akit manapság leginkább az általa készített függvénytáblázatokról ismernek) arra, hogy semelyik csempemintának nem lehet egynél több ötszörös forgási szimmetriacentruma. A bizonyítás a következô: Tegyük fel, hogy egynél több van. Válasszuk ki azt a kettôt, A t és B-t, melyek a legközelebb vannak egymáshoz (3. ábra). Forgassuk el B körül a mintázatot 360/5=72 fokkal az óramutató járásával megegyezô irányban, A t az A'-be víve, ahogy az ábrán látható. Ezután forgassuk el az eredeti mintázatot A körül 72 fokkal, most az óramutató járásával ellenkezô irányban, B-t B'-be víve. Az eredmény: mindkét forgatás (indirekt feltevésük szerint) változatlanul hagyja a mintázatot. Ekkor azonban lenne két szimmetriacentruma, A' és B', melyek közelebb vannak egymáshoz, mint A és B. Ez ellentmond annak a felvetésünknek, hogy A és B az egymáshoz legközelebb levô szimmetriacentrumok.
 |
 |
| 3. ábra. Barlow bizonyítása arra, hogy egy csempemintának sem lehet két ötszörös szimmetriacentruma |
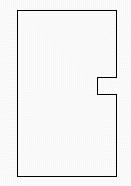
4. ábra. A Conway-csempe, amely 0-féleképpen csempéz |
Vannak olyan csempék (és csempekészletek), melyekkel csak egyféleképpen csempézhetô periodikusan a sík, például a szabályos hatszög vagy a kereszt alakú pentomino. Egy tetszôleges háromszög vagy paralelogramma megszámlálhatatlanul végtelen sokféleképpen csempéz. Grünbaum és Shephard sejtése az, hogy nincs olyan csempe, ami megszámlálható végtelen sokféleképpen csempéz periodikusan. Azt is sejtik, hogy tetszôlegesen adott r pozitív egész esetén van olyan csempe, amely pontosan r-féleképpen csempézi a síkot. Az r=1-tôl 10-ig esetekhez már találtak ilyen csempéket. Elôadása során Conway bemutatta azt, amit õ "Conway-csempének" nevez, az r=0 esethez (4. ábra). Avval zárta az elôadást, hogy ez volt az elsô valaha is tartott elôadása a Penrose-csempézésrôl, ahol nem mondott véletlenül "sárdákat és dárkányokat".
Fordította:
TÖRÖK JUDIT
| Penrose-csempézés | Elsõ rész/1 Elsõ rész/2 Második rész |
| Természet Világa, | 128. évf. 8. sz. 1997. szeptember, 396-399. o. |
| https://www.kfki.hu/chemonet/TermVil/ | |
| https://www.ch.bme.hu/chemonet/TermVil/ |