BIOLÓGIA
SCHEURING ISTVÁN
Kaotikus jelenségek a biológiában
Elôzô rész
Kaotikus populációk
Térjünk át egy magasabb szervezõdési
szint, a populációk és közösségek
tanulmányozására. Vizsgálati egységünk
az egy fajhoz tartozó potenciális szaporodási közösséget
alkotó élõlények összessége: a
populáció. Mivel az ökológus arra kíváncsi,
hogy bizonyos fajok populációi miért élnek
együtt, miért éppen a megfigyelt arányokban vannak
jelen, ill. mások miért nem tudnak fennmaradni egy adott
helyen, ahhoz, hogy e kérdéseket meg tudjuk ragadni, szükség
van a populációk dinamikai leírására.
Tekintsünk egy külsõleg és viselkedésében
is igen egyszerû modellt. Legyen egy adott területen a t-edik
évben a vizsgált populáció egyedeinek száma
N(t), és jelöljük r-rel az egy egyedre
vonatkoztatott szaporodási rátát. Nyilván
a populáció a véges tápanyagforrások,
hely, vízkészletek stb. miatt nem fog a végtelenségig
azonos ütemben növekedni. Minél több egyed van a
vizsgált helyen, annál kisebb mértékben fog
a populáció szaporodni. Tehát az r szaporodási
ráta, az N(t) a populáció egyedszámának
növekedése miatt csökkenni fog. Itt nem részletezhetõ
okok miatt érdemes az r=r0 /(1+aN(t))b
összefüggést választani, ahol r0
a populáció egyedszámától független
növekedési ráta, az a és a b pozitív
állandók. Az a paraméter szerepe számunkra
most nem fontos, a b paraméter nagysága az egyedek
közötti vetélkedés erõsségét
adja meg. Ezek után a populáció denzitását
a t+1-edik évben az N(t+1)=r0N(t)/(1+aN(t))b
képlet határozza meg. Legyen a=1, b=8,8, s vizsgáljuk
meg modellünk viselkedését különbözõ
r0 értékek esetén.
 |
 |
 |
 |
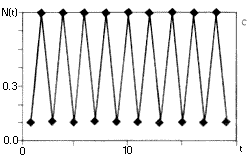 |
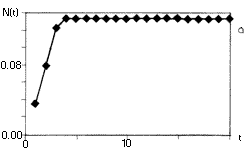
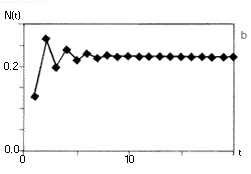
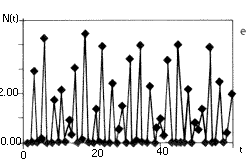
6. ábra. A szövegben ismertetett
populációdinamikai modell, a
nemlineáris rendszerek viselkedésének
széles skáláját mutatja. Az (a, b) ábrán
egy rögzített értékhez tart a populáció
mérete, r0= 3, ill. r0= 6. A (c, d) esetben
periodikusan oszcillál, r0= 16, r0= 26.
Az (e) ábrán a populáció mérete
rendszertelenül váltakozik, r0= 100.
A determinisztikus egyenlet véletlenszerû
viselkedést mutat, a rendszer kaotikus |
A 6. ábra tanúsága szerint a fenti képlet
az r0 paramétertõl függõen
igen sokféle viselkedést mutathat: tarthat monoton módon
vagy lecsengõ osszcillációval az egyensúlyi
egyedszámhoz (6. a, b ábra), lehet periodikus (6.
c, d ábra), és ha a r0 elég
nagy, viselkedhet kaotikusan is (6. e ábra ). (Ezért
nevezik az r0-t a rendszer kontroll vagy bifurkációs
paraméterének). Nem csupán ez, az egyébként
igen egyszerû populációdinamikai modell jósol
kaotikus viselkedést bizonyos paramétertartományban,
hanem számtalan gazda – parazita, zsákmány – ragadozó
is, és a kompetíciós modellben is kimutatták
a káosz jelenlétét. Ez nem meglepõ, hiszen
a populációk egyedszámának változását
jelentõsen befolyásolják az egyedek közötti
tipikusan nemlineáris kölcsönhatások. Felvetõdik
a kérdés, hogy a valóságos populációkból
származó adatsorok mutatnak-e kaotikus viselkedésre
utaló jegyeket. Sajnos igazán egyértelmû választ
most sem tudunk adni, mivel a rendelkezésre álló populációs
adatsorok túl rövidek, ráadásul külsõ
környezeti zajokkal és mintavételi hibákkal terheltek.
Megtehetõ például, hogy az imént bevezetett
modell r0 és b paramétereit megbecsüljük
egy valós adatsorból, majd az így kapott képlet
által generált adatok viselkedését vizsgáljuk.
Hassel és munkatársai 1976-ban 24 terepi és
laboratóriumi adatsort elemeztek ily módon. Nem kis meglepetésükre
egyetlen adatsort találtak, amely a fenti módszer alapján
kaotikus volt. Ráadásul a kaotikus adatok sem valamilyen
természetes, hanem laboratóriumi populációtól
származtak. Azóta jó néhány, ennél
kifinomultabb adatsorelemzési eljárást is kifejlesztettek,
de az általános következtetés alig változott:
bár a periodikus viselkedés gyakori, káoszgyanús
populációs adatsor mindmáig alig féltucatnyi
van. Ennek (a statisztikai eljárások bizonytalansága
mellett) két, egymástól független oka van. Egyrészt
a kaotikus populációk gyakran nagyon kicsi egyedszámra
esnek vissza (6 e. ábra), így a környezeti zavarok
könnyen kipusztíthatják e populációkat.
Ennél meggyõzõbb érv, hogy a valódi
élõhelyek mozaikosak, amelyek között az egyedek
vándorolnak, továbbá az egyedek életciklusa,
szaporodási stratégiája is sokkal összetettebb,
mint ahogy azt általában a modellekben feltételezik.
Megmutatható, hogy mindezek a tulajdonságok jelentõsen
csökkentik a káosz kialakulásának az esélyét
(lásd pl. Scheuring és Jánosi, 1996). Nem véletlen,
hogy a kaotikus adatsorok jó része laboratóriumi körülmények
között nevelkedõ vagy valamilyen „természetidegen”
környezetben élõ populációkból
származnak. Ez utóbbira példát a new yorki
kanyaróvírus szolgáltat. A kanyaró az egyik
leghatékonyabban fertõzõ betegség, s egy olyan
nagyváros, mint New York, hatalmas “homogén élõhely”
a számára. Ebben a homogén környezetben, ahogy
azt a 7. ábra is szemlélteti, a regisztrált
megbetegedések száma igencsak rendszertelenül változik.
Errõl az adatsorról rengeteg elemzés készült
már, de ebben az esetben sem dönthetõ el egyértelmûen,
hogy a komplex viselkedés mögött (kevés dimenziós)
káosz vagy külsõ környezeti zaj húzódik-e
meg. Mindenesetre a káosz jelenlétét valószínûsíti
az, hogy más gyerekbetegségek (pl. mumpsz, bárányhimlõ)
egyértelmûen periodikusan viselkednek, továbbá
egyes kanyarófertõzésekhez tartozó adatsorok
kaotikusságot (New York, Koppenhága), mások (pl. Nagy
Britannia) periodikusságot mutatnak. Megjegyzendõ, hogy járványtani
szempontból lényeges kérdésrõl van szó,
hiszen más az optimális oltási stratégia, ha
a betegségek kaotikusan, és más, ha periodikusan jelentkeznek.

7. ábra. A New York-i (a) és koppenhágai
(b) kanyarómegbetegedések száma
1928-és 1964,ill. 1968 között hónaponkénti
bontásban.
Az idõsorelemzések a kevés dimenziós káosz
jelenlétére
utalnak (London és Yorke, 1973 adatai alapján)
Kerüli-e a természet a káoszt?
Mivel a biokémiai, biológiai folyamatok alapvetõen
nemlineárisak, ezért egy merõben új gondolkodásmód
kialakítására van szükség. Ilyenkor a
részkomponensek viselkedésébõl általában
nem lehet a nagyobb szervezõdési egység tulajdonságait
megmondani. A dinamikai paraméterek apró változása
nem szükségszerûen okoz kis változást a
rendszer állapotán, mi több, ha a rendszer kaotikus,
akkor a rendszer viselkedése is csak igen korlátozott mértékben
jósolható.
Láttuk azt is, hogy a biológiai rendszerek leginkább
extrém vagy patologikus esetekben válnak kaotikussá,
ill. erõsen oszcillálóvá. A korábban
említett epilepszián és szívaritmián
kívül számos olyan betegséget ismerünk,
amikor a tüneteket a rendszer dinamikai állapotának
megváltozása okozza. A fehérvérûségnek
van egy olyan fajtája, aminek jellemzõje, hogy mind a fehérvérsejtek,
mind a trombociták mennyisége periodikusan oszcillál.
A számos további példa közül megemlíthetõ
a Cheyne –Stokes-légzés. A beteg ilyenkor igen
gyorsan, periodikusan lélegzik (hiperventilláció).
E jelenség általános oka, hogy a légzést
gátló idegi szabályozásban valami zavar keletkezett.
Az összes példában a dinamikai rendszer elemei közötti
kapcsolat változása okozza a betegséget,
ezért az ilyen jellegû megbetegedéseket összefoglalva
dinamikai betegségeknek nevezik. A korábban elmondottak
alapján úgy tûnik, mintha normális esetben a
természet kerülné a káoszt. Lehet, hogy ez valóban
így van, azonban a jelenlegi adatsorok birtokában nem dönthetõ
el, hogy a biológiai rendszerekben az alacsonydimenziós káosz
ritka jelenség-e vagy sem.
Ha valamilyen oknál fogva véletlenszerû jelekre
van szükség, akkor ezt egy kaotikus rendszer hatékonyan
megvalósítja. Megmutatható, hogy egyes konfliktushelyzetekben
akkor viselkedik az élõlény optimálisan, ha
egy-egy viselkedési stratégiát bizonyos valószínûséggel
követ. Legismertebb példa az ún. héja–galamb
játék. A modellben a küzdelem valamilyen fontos
forrásért folyik. Az állatok kétféle
stratégiát alkalmazhatnak. Héjaként minden
esetben azonnal támadnak s verekszenek, amíg meg nem sérülnek
vagy le nem gyõzik a másikat. A galamb elmenekül, ha
rátámadnak, míg két galamb-stratégiát
folytató között a forrás véletlenszerûen
oszlik meg fele-fele arányban. Ha a sérülés okozta
kár nagyobb, mint a forrásból származó
nyereség, akkor az az állat jár a legjobban, amelyik
a héja-stratégiát a nyereség és a kár
arányában véletlenszerûen alkalmazza. Ilyenkor
nagyon hasznos lehet egy agyba épített “véletlenszám-generátor”.
Ha a döntés elõtt ennek az értéke nagyobb,
mint az optimális viselkedés alapján beállított
érték, akkor a héja-viselkedést követi
az állat, ha kisebb, akkor a galambét.
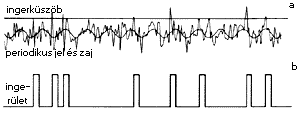
8. ábra. A zaj szerepe a gyenge jelek érzékelésében.
Ha az érzékelõ receptorra
érkezõ periódikus jel (itt egy szinuszhullám)
nem éri el az ingerküszöböt
(vízszintes vonal), akkor nem detektálható (a). Egy
független “zaj” hozzáadásával
az ingerküszöböt idõnként, s többé-kevésbe
periodikusan átlépve, a jel érzékelhetõvé
válik (b)
Egy kísérletileg igazolt biológiai
esetrõl is tudunk, amikor a zaj kifejezetten elõnyös.
A rákok kültakaróján mozgást érzékelõ
sörték találhatók. Segítségükkel
az állat érzékeli a víz mozgását,
így idõben felfedezi a ragadozó közeledtét.
A közeledõ állat hullámokat kelt, mely periodikusan
érkezik a receptorhoz. A receptorok egészen csekély
mozgást is jeleznek, amit egy speciális módszerrel
érnek el. Egy folyami rák fajon (Procambarus
clarkii) kimutatták, hogy az érzékelõrendszerhez
tartozó neuronok belsõ zajt keltenek, ami hozzáadódva
az egyébként érzékelhetetlenül gyenge
periodikus jelhez, esetenként átlépik az ingerküszöböt,
s így ingerületként továbbítódnak
(8. ábra). Könnyen lehet, hogy a szükséges
“zajt” egy kaotikus neuronhálózat kelti. Az is valószínû,
hogy az érzékelésben és általában
a biológiai információ-feldolgozásban fontos
szerep jut a belsõ “zajnak”. Akkor viszont az sem kizárt,
hogy szervezetünk számos apró kaotikus alrendszert rejt
magában.
Irodalom
Goldberger, A.L, Rigney, D. R. és West, B. C. (1990) Káosz
és fraktálok az emberi szervezetben. Tudomány, április,
28-36.
Hassel, M. P, Lawton, J. H, és May, R. (1976) Patterns of dynamical
behaviour in single-species populations. J. Anim. Ecol. 45: 471-468.
Holden, A. V. (szerkesztõ) (1986) Chaos. Manchester University Press
Scheuring, I. és Jánosi I. M. (1996) Az eltûnõ
káosz nyomában: Miért nem kaotikusak a valóságos
ökológiai rendszerek? Fizikai Szemle. Biológiai Fizika
Különszám. II/7 235-241.
Strogatz, S. H. (1994) Nonlinear dynamics and chaos. Addison-Wesley Publ.
Comp.
Wiesenfeld, K. Moss, F. (1995) Stochastic resonance and the benefits of
noise: from ice ages to crayfish and SQUIDS. Nature, 373: 33-36.
| Természet Világa, |
129. évf. 8. sz. 1998. augusztus, 338–342. o.
https://www.kfki.hu/chemonet/TermVil/
https://www.ch.bme.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez






