
|
|
 |
SCHEURING ISTVÁN
Kaotikus jelenségek a biológiában
A klasszikus természettudományos világkép szerint, ha egy rendszert néhány egyértelmûen megadható kapcsolat határoz meg, akkor a rendszer jövõbeni viselkedése egyértelmûen megadható. A hatvanas évek eleje óta köztudott, hogy ez a várakozásunk számos esetben ábránd marad. Kiderült, hogy az ún. nemlineáris rendszerek számos érdekes tulajdonságokkal rendelkeznek. Legmeglepõbb jellemzõjük, hogy ilyen esetekben a kevésváltozós determinisztikus rendszerek is viselkedhetnek véletlenszerûen, kaotikusan. A biológiai folyamatok döntõ többségét viszont a nemlineáris kapcsolatok határozzák meg. Ennek alapján várható, hogy számos biológiai rendszer viselkedhet kaotikusan. Írásomban a káoszelméleti alapfogalmak ismertetése mellett olyan biológiai jelenségeket, kísérleteket gyûjtöttem össze, ahol a káosz léte gyanítható vagy legalábbis erõsen feltételezhetõ. Mint látni fogjuk, jelenlegi tudásunk alapján nem dönthetõ el, hogy a káosz ritka vagy gyakori jelenség-e az élõvilágban.
Nem kétséges, hogy Neumann János volt századunk egyik legkiválóbb matematikusa, aki híres “minimax” tételének bizonyításával (ekkor még csak 23 éves) nagy lökést adott egy új s azóta látványos sikert befutott matematikai elméletnek, a játékelméletnek, de jelentõs szerepe volt a kvantummechanika matematikai megalapozásában is. A számítógépek még ma is az õ elméleti megfontolásai alapján épülnek. Részt vett az elsõ számítógépek megalkotásában, azzal a nem titkolt reménnyel, hogy így lehetõsége nyílik például az idõjárás elõrejelzésére, mi több, annak befolyásolására is. Neumann János tévedett, s mily különös, tévedését Edward Lorenz amerikai meteorológus pontosan a Neumann-féle számítógép egy nem túl késõi utódjának a segítségével mutatta ki.
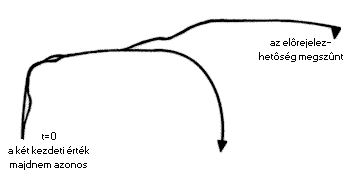 |
| 1. ábra. Kaotikus rendszerben a kezdeti állapot kicsi különbségei igen gyorsan földuzzadnak. A pályák az idõ exponenciális függvénye szerint távolodnak egymástól, ezért a kezdeti értékbõl hosszú távú jóslás nem tehetõ |
Lorenz egy jelentõsen leegyszerûsített meteorológiai modellel dolgozott. Összesen három szabad változója volt, s ezek idõbeli változását egy közönséges differenciálegyenlet-rendszer határozta meg. A modellt, amely már a “ceruza és papír” módszerrel is kezelhetetlen volt, számítógépes szimulációkkal tanulmányozta. A program elején kezdeti értékeket adott a változóknak, majd a gép apró elemi lépésenként kiszámította, hogyan alakul a változók értéke az idõ függvényében. A ‘60-as évek elején járunk, amikor a számítógépek még igencsak megbízhatatlanok voltak, ezért Lorenz ugyanazon kezdeti értékek mellett többször is lefuttatta a programot. Meglepve tapasztalta, hogy minden esetben más-más eredményt kapott, ráadásul az eredmények láthatóan minden szabályszerûség nélkül változtak. Elõször természetesen programozási vagy géphibára gyanakodott. Végül rájött, hogy a kezdeti értékek mégsem voltak teljesen azonosak, mivel csak négy tizedesjegy pontossággal adta meg az értékeket, s a gép a maradék négy helyiértékre véletlenszerûen írta be a számokat. Az eltérés a kezdeti értékek között 10-5 nagyságrendû volt, az állapotok között mégis egyre nagyobb és nagyobb különbségek keletkeztek (1. ábra). Ez az ún. pillangó effektus: a kezdetben kicsi értékkülönbségek óriási eltéréseket okozhatnak rövid idõ alatt. Ezt szemléletesen a következõképpen is megfogalmazhatnánk: ha egy lepke megrebbenti a szárnyát Pócsmegyer határában, az Bordeaux-ban vihart okozhat egy héttel késõbb. Tehát az idõjárás hosszabb távú elõrejelzésére csak akkor van lehetõség, ha az aktuális állapotot nagyon pontosan tudjuk. Ez mai ismereteink szerint reménytelen feladatnak tûnik (lásd a Természet Világa, Idõjárás és elõrejelzés 1998. évi I. különszámát.
Mi a káosz?
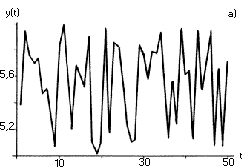
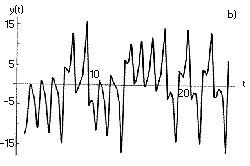
Az elõzõ fejezet tanulságait összefoglalva azt mondhatjuk; vannak olyan kevés változót tartalmazó determinisztikus rendszerek, amelyek nagyfokú érzékenységet mutatnak a kezdeti értékekre. Mivel a kezdeti állapotból tökéletesen soha sem ismert, a rendszer véletlenszerû, kaotikus viselkedést mutat. Példaként gondoljunk arra, hogy egy hegyére állított ceruza hogyan dõl el. Ha a ceruza kezdeti helyzetét egy kicsit is megváltoztatjuk, akkor az egészen más helyen fog földet érni, mint eredetileg, mozgását tehát nem tudjuk megjósolni. Ebben a mechanikai rendszerben csak ez az egy kezdeti állapot ilyen különleges tulajdonságú, és csak a mozgás egy véges idõtartamára igaz, hogy a közeli pályák gyorsan távolodnak egymástól. A véletlenszerû viselkedést mutató kaotikus rendszerekben minden, vagy legalábbis végtelen sok kezdeti állapot esetén és a mozgás egész idõtartamára igaz az, hogy a kezdetben közeli pályák gyorsan távolodnak egymástól. Kérdés azonban, hogyan ismerhetõ fel a kaotikusság és hogyan különíthetõ el a belsõ dinamikai bonyolultság a rendszeren a kívülrõl jövõ, sokváltozós “zajtól”. A zaj markánsan megkülönböztethetõ a káosztól, ha a rendszer változóinak terében, az ún. fázistérben vizsgáljuk a mozgást. (Például, ha egy biokémiai folyamatban három anyag: x, y és a z koncentrációját mérjük, akkor az x, y, z változók terében a rendszer állapota egy idõpillanatban egyetlen pont lesz. A folyamat során ez a pont fog vándorolni az x, y, z által meghatározott fázistérben.) Ahogy azt a 2. ábra szemlélteti, a zajos rendszer a fázistérben egy szétkent pacni lesz, míg a kaotikus rendszer egy sajátos “valamin”, a kaotikus attraktoron fog mozogni. Sajnos a gyakorlatban nem ilyen szembeötlõ a különbség, mert a kaotikus vagy periodikus rendszerbõl származó adatok más külsõ zajokkal terheltek, így sokszor igen nehéz lehámozni a kevés változós determinisztikus hatást a külsõ sokváltozós zajról. (Az írásban a káosz kimutatására kifejlesztett matematikai eljárásokat nem mutatjuk be, azonban ha egy adatsorról azt állítjuk, hogy az kaotikus, akkor e kijelentés mögött mindig részletes matematikai analízis áll.)
 |
 |
 |
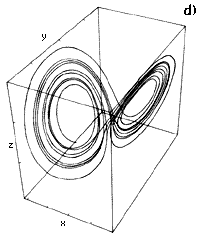 |
2. ábra. A kaotikus és a sokváltozós véletlenszerû, rendszer tulajdonságai. Míg az egyes dinamikai változók mind a véletlenszerû (a), mind a kaotikus rendszerben (b) rendszertelenül változnak, addig a mozgás változóinak terében (itt x,y,z -vel jelölve) a kaotikus rendszer egy jellegzetes “valamin”, a kaotikus attraktoron (c), a véletlenszerû pedig egy elkent felhõn mozog (d). Ebben a példában a Lorenz-egyenletek különös attraktora látható
Egy számunkra lényeges pontról eddig nem ejtettünk szót. Ez a következõ: ahhoz, hogy egy dinamikai rendszer kaotikus viselkedést mutasson, alapvetõen fontos, hogy a változók nemlineáris kapcsolatban legyenek egymással. Lineáris egy x, y, z stb. változókkal leírt rendszer, ha e mennyiségek változását (elsõ hatványon lévõ) a tagok összegei határozzák meg (azaz ax+by+cz+d, ahol a, b, c, d valós számok). Nemlineáris rendszerekben magasabb hatványok, nemlineáris függvények is szerepelhetnek (pl. xy, z2x, sinx stb.). A biokémiai, biológiai rendszerek nemlineárisak a reakcióhálózatok, a szervek és szervrendszerek közötti anyag- és információáramlás, valamint a populációk egyedei közötti kölcsönhatások miatt. Várható tehát, hogy a természetben jónéhány olyan jelenséggel találkozhatunk, ami alapjaiban determinisztikus jellegû, a rendszer mégis véletlenszerûen viselkedik.
A továbbiakban néhány kaotikus biokémiai rendszerben kutatunk a káosz után, majd az ideg- és a szívmûködésben tapasztalható nemlineáris jelenségeket tekintjük át. Végül megnézzük azt is, hogy a populációk egyedszámváltozása mögött lehet-e kaotikus viselkedést sejteni. A cikk végén ismereteink alapján megpróbálunk választ adni arra, hogy a káosz gyakori vagy ritka jelenség-e a biológiában.
Káosz a kémiai, biokémiai rendszerekben
A nagy felfedezéseket gyakran fogadja elutasítás, idegenkedés, fõleg akkor, ha az újdonság nem a tudomány valamelyik “fellegvárából” érkezik. Pontosan ez történt Borisz Belouszov orosz biokémikussal is az ötvenes évek elején, amikor a Krebs-ciklus nagyon leegyszerûsített változatát tanulmányozta kémcsõben. Citromsavat és bromátionokat vegyített kénsavoldatban cérium katalizátor jelenlétében. Megdöbbenéssel tapasztalta, hogy a keverék rövid idõn belül sárga lett, majd kb. egy perc múlva színtelenné vált, majd megint sárgává, s ez az oszcilláció több mint egy órán keresztül folytatódott. Ez a jelenség abban az idõben annyira ellentmondott az általános felfogásnak és tapasztalatnak, hogy a tudományos világtól elzárt Szovjetunióban élõ Belouszov képtelen volt eredményeit megjelentetni nemzetközi szakfolyóiratban. Megfigyelését végül egy szovjet orvosi találkozó orosz nyelvû kiadványában sikerült közölnie. Természetesen eredményeirõl a szakma továbbra sem vett tudomást, mígnem egy fiatal doktorandusz, Zsabotyinszkij többször megismételve Belouszov kísérleteit, 1968-ban egy prágai nemzetközi konferencián be is mutatta az oszcilláló reakciót. Ekkorra már a tudósvilág figyelme a nemlineáris jelenségek felé fordult, így az elõadás sikere óriási volt. Belouszov, aki egy új tudományágat indított útjára, két év múlva meghalt, Zsabotyinszkij viszont a Szovjetunió ünnepelt tudósa lett.
Késõbb kimutatták, hogy ezekben a rendszerekben az oxidáció, vékony haladó hullámfrontok mentén terjed és a hullámok találkozásukkor kiolthatják egymást. Érdemes megjegyezni, hogy e jelenség kísértetiesen hasonlít arra, ahogyan az ingerülethullámok viselkednek a szív- és az idegszövetekben. Mi több, ha a reakció az oldat folytonos átáramoltatása mellett játszódik le, akkor bizonyos áramlási sebességek esetén a reagensek koncentrációja kaotikusan változik.
 |
| 3. ábra. Glükóz periodikus bevitele esetén
(alsó ábra) a NADH-koncentráció szabálytalanul fluktuál (felsõ ábra). Az adatok elemzésével megmutatható, hogy a rendszer kaotikus (Rapp, 1986 nyomán) |
Mégsem ez, hanem egy enzimreakció volt az elsõ bizonyítottan kaotikus kémiai reakció. Olsen és Degn, dán bikémikusok a NADH (az ATP-hez hasonlóan energiatároló szerves molekula) oxidációját vizsgálták peroxidáz katalizátor jelenlétében. Az oldat folyamatos keverése közben az O2 passzív diffúzióval jutott be a rendszerbe, közben a NADH-t folyamatosan táplálták az oldatba. A reakció nagyobb peroxidáz enzimkoncentráció esetén oszcillációt, míg kisebb koncentrációk mellett kaotikus viselkedést mutatott. Bár e kísérlet továbbra is csak egyszerû “karikatúrája” az élõ sejtekben lezajlódó kémiai folyamatoknak, az régóta köztudott, hogy periodikus kémiai oszcilláció számos sejtkultúrában vagy sejtpreparátumban megfigyelhetõ. Így pl. a glikolízis vagy a sejten belüli Ca-cAMP (calcium-ciklikus AMP) intermedierjei idõben oszcillálnak. A reakciókat mindkét esetben allosztérikus enzimek szabályozzák, azaz a reakcióháló egyes elemei ezen enzimekhez kapcsolódva aktiválják (bekapcsolják) vagy gátolják (kikapcsolják) azokat. A glikolízis folyamatára sikerült egy meglepõen egyszerû, a kísérletekkel összhangban lévõ matematikai modellt is készíteni. A modell szerint a glukóz állandó beáramlás esetén oszcilláló termékkoncentráció (pl. ATP, vagy NADH) várható, míg a glükóz periodikus adagolása kaotikusan változó termékkoncentrációt okozhat. A fenti eredménnyel teljes összhangban élesztõgomba (Saccharomyces cerevisiae) sejtpreparátumokon sikerült kimutatni, hogy a NADH mennyiség valóban mutathat kaotikus jelleget, ha a glükóz periodikusan áramlik a rendszerbe (3. ábra).
Tehát az oszcilláló nemlineáris kémiai hálózatok könnyen kaotikussá válhatnak, ha a bemenõ anyagok koncentrációja is oszcillál. Ezek szerint ha két (vagy több) oszcilláló ciklust összekapcsolunk, kaotikus rendszerekhez juthatunk. A sejtben igen sok ilyen kapcsolat létezik, várható tehát, hogy kaotikus jelenségek nem csupán a vegyészek kémcsövében, hanem az élõ sejtek kémiai hálózatában is elõbb-utóbb megfigyelhetõk lesznek. A periodikus viselkedés, ill. a periodikusan viselkedõ nemlineáris alrendszerek összekapcsolódása magasabb szervezõdési szinteken még szembeötlõbb. A legismertebb, általában periodikus viselkedést mutató sejtrendszerek: az idegrendszer és a szív. Ennek alapján nem kizárt, hogy bizonyos körülmények között mind a szív, mind az idegrendszer kaotikussá válhat.
Kaotikus idegrendszer, kaotikus szív
 |
| 4. ábra. A tintahal óriásaxonján mért elektromos jel kaotikus (felül), ha periodikus elektromos impulzu- sokkal ingereljük (alul). A mérések szerint a membránpotenciál kaoti- kusan oszcillál (Aihara és Matsumoto, 1986 nyomán) |
Az elõzõ fejezetben nem véletlenül került szóba a Ca-cAMP-ciklus. A cAMP a sejten belüli kommunikáció egy fontos eleme. A sejten kívülrõl érkezõ hormonutasítás a sejtmembránban lévõ adenilát-cikláz enzimet aktiválja, ami ATP-bõl cAMP-t állít elõ. A cAMP pedig más citoplazmatikus vagy membránenzimeket aktivál. Kimutatták azt is, hogy a cAMP felszabadítja a sejtben a fehérjékhez (pl. a kalmodulinhoz) kötött Ca2+-ionokat, így hozzájárul a membrán két oldala közötti potenciálkülönbség megváltozásához. A Ca2+-ion viszont gátolja az adenilát-cikláz aktivitását, míg a Ca-kalmodulin komplex serkenti azt. Tehát egy összetett szabályozórendszerrõl van szó, ami kapcsolatban áll a sejt polarizációs állapotával. Az idegsejtek elektromos aktivitását, ill. állapotát pontosan a membrán két oldala közötti potenciálkülönbség határozza meg, következésképpen az idegsejtek elektromos viselkedését befolyásolja a példaként említett Ca-cAMP-ciklus dinamikai jellege. Matematikai megfontolások alapján valószínûsíthetõ, hogy a Ca-cAMP ciklus periodikus vagy akár kaotikus is lehet, tehát a neuronaktivitás kaotikussága szintén elképzelhetõ. Megerõsíti ezt a gyanút, hogy az idegsejtek elektromos viselkedésének leírására szolgáló modellek bizonyítottan kaotikus impulzuskibocsájtást eredményezhetnek, ha a rendszert periodikus jellel ingereljük. Ez az a pont, ahol az elvi fejtegetések összekapcsolódnak a kísérletekkel. Számos alacsonyabb rendû állat preparált idegsejtjében (pl. tintahal óriás axonjában) sikerült ugyanis kimutatni, hogy periodikus külsõ elektromos ingerlés hatására a kimenõ elektromos jel kaotikussá válik (4. ábra).
Valószínûsíthetõ tehát, hogy az élõ szervezetben (ahol a rengeteg idegsejt komplex szövevényt alkot), lehetnek olyan “idegsejt alhálózatok”, melyekben egyesek periodikus jeladóként, mások kaotikus rezonátorként viselkednek. E feltevés elvileg megvizsgálható az agyhullámok elemzésével vagy egyszerû pszichológiai tesztekkel is. Ha ugyanis az agy egyetlen feladatra összpontosít, akkor csak korlátozott területe kerül aktív állapotba. Jól ismert kísérleti összeállítás az, amikor a résztvevõknek egymás után sokszor elõre meghatározott ideig (pl. 3 vagy 5 másodpercig) gombot kell lenyomva tartanak. Az az idõ, amíg a gombot lenyomva tartják, az adatsor egy eleme. Ennek alapján (legalábbis elvileg) többé-kevésbé meghatározható, hogy az eltérések mögött egy sokváltozós zajos vagy egy néhány változót tartalmazó kaotikus idegmûködést van-e. Érdekes, hogy az említett adatok értelmezése nem egyértelmû. Sokan igazoltnak vélik a káosz jelenlétét az idegrendszerben, mások úgy látják, hogy az elemzésekbõl inkább egy sokváltozós véletlenszerû rendszer jelenléte olvasható ki. Az idegrendszer sajnálatosan gyakori rendellenessége az epilepszia. Az elnevezés számos egymástól különbözõ idegrendszeri probléma és tünetegyüttes összefoglaló neve. Bizonyos esetekben a beteg agyának meghatározott részébõl terjed szét a zavar a roham idején. Ilyenkor az epileptikus “mag” két roham között is folyamatosan megtalálható az agyban. Állatkísérletekkel kimutatták, hogy ha bizonyos anyagokat (pl. penicilint) közvetlenül juttatnak az agykéreg egy részébe, akkor kiváltható az imént említett ún. fokális epilepszia. Megmutatható, hogy a penicilin hatására az idegsejtek közötti kémiai szinapszisok erõssége megnõ. A kóros területen tehát túl aktív sejtek valószínûleg túlérzékeny kapcsolatokat tartanak fenn. Elképzelhetõ, hogy a krónikus mag, erõs periodikus jeleket kiadva magából, nagy agyi területet kényszerít oszcilláló vagy kaotikus viselkedésbe. Nem állítjuk, hogy az epilepszia az agy kaotikus állapota, inkább az valószínûsíthetõ, hogy a tünet az idegrendszer védekezése a kaotikus állapot kialakulása ellen.
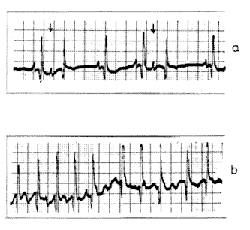 |
| 5. ábra. Aritmiás betegek EKG grafikonjai. A tüneteket egy második pacemaker megjelenése okozza. (a) Néha a normális ritmusnál kisebb frekvenciájú, extra összehúzódások jelentkeznek. (b) Pitvari fibrilláció. Nagyon gyors mozgás, rendezetlen állapot. Egyes elemzõk szerint a háttérben kaotikusjelenségek sejthetõk (Ganong, 1989 nyomán) |
A legismertebb nemlineáris oszcillátor a szív. Periodikus összehúzódásait és elernyedéseit a pacemaker sejtekbõl kiinduló elektromos hullámok vezérlik. A pacemaker sejtek normális esetben a jobb pitvar ún. szinuszcsomójában találhatók. A szívben lévô összes elektromosan aktív sejt között a szinuszcsomó sejtjei adják a legnagyobb frekvenciájú impulzust, ezért a többieket megelõzve karmesterként diktálják az ütemet. A korábban elmondottak alapján – gondolom – nem meglepõ, ha azt várjuk, hogy több pacemaker központ jelenléte esetén vagy külsõ periodikus gerjesztés hatására a szívingerületek kaotikussá válhatnak. Ezt az elképzelést támasztja alá a beteg szív gyakori tünetegyüttese, a szívaritmia. A tüneteket az elektrokardiogramm (EKG) hullámok ritmusa és alakja alapján számos csoportra bontják. Van, amikor a normális összhúzódások közé újak iktatódnak be, egyes súlyos esetekben viszont az EKG teljesen szabálytalan képet mutat (5. ábra). Az adatok elemzése alapján a legvalószínûbbnek az látszik, hogy a szabálytalanul mûködõ szív kaotikus, bár érdekes módon egyes elemzések alapján az egészséges szív is “gyengén” kaotikus viselkedést mutat. Köztudott, hogy az aritmiát leggyakrabban egy második pacemaker központ megjelenése okozza. Két karmester esetén a zenekar több ritmust is követhet (5. a ábra), de ha mindketten elég határozott jellemek, az is megeshet, hogy az együttes zûrzavarosan játszik (5. b ábra). A klinikai megfigyelések mellett közvetlen kísérletek is alátámasztják, hogy a többközpontú szívritmusszabályozás hevesen oszcilláló vagy kaotikusan mûködõ szívhez vezethet. A nyolcvanas években több kutatócsoport is végzett csirkeembriók szívszövetein ilyen irányú kísérleteket. A kiválasztott preparátumok önálló periodikus elektromos aktivitást mutattak. Ezután mikroelektródokat helyeztek a szövetdarabba, és azon keresztül kívülrõl periodikusan ingerelték a preparátum sejtjeit. Eközben mérték a preparátum elektromos aktivitását is. A külsõ gerjesztés frekvenciájának függvényében, a klinikai tapasztalatokkal teljes összhangban, mind az extra jeladást, mind a kaotikus elektromos aktivitást meg lehetett figyelni. Természetesen e kisérletek csupán leegyszerûsített modelljei a valóságnak, hiszen sem a pacemaker központok kölcsönhatását, sem a felsõbb idegi szabályozást, sem a szív bonyolult struktúráját nem veszik figyelembe.
| Természet Világa, | 129. évf. 8. sz. 1998. augusztus, 338–342. o. https://www.kfki.hu/chemonet/TermVil/ https://www.ch.bme.hu/chemonet/TermVil/ |