
3. ábra. Az 1-metil-adenin három izomer szerkezete
| KÉMIAI NOBEL-DÍJ, 1998 | KVANTUMKÉMIA |
FOGARASI GÉZA – SZALAY PÉTER
Számítógéppel a molekulák nyomában
Magyarok az élvonalban
Miként a fentiekbôl is sejthetô, a Nobel-díj ez alkalommal nem egyetlen zseniális, merõen új eredményt értékelt, hanem bizonyos értelemben a kvantumkémia egészének fejlôdését ismerte el. Elfogulatlanul állítható, hogy ebben a folyamatban magyar kutatók is igen jelentôs szerepet játszottak. Számos nevet lehetne említeni, de talán két kutató az, akiknek neve legvalószínûbben bekerült volna egy ilyen ismertetésbe akkor is, ha az külföldön íródik.
A DFT-módszerrel kapcsolatban már említettük annak elôdjét, Slater Xa-módszerét, mely más filozófiával, de lényegét tekintve ugyanazt csinálta, mint a Kohn–Sham-módszer. Ezen a területen Gáspár Rezsô publikált fontos eredményt még az 1950-es években, melynek alapján a Kohn–Sham-módszert Slater többször és egyértelmûen Gáspár–Kohn–Sham-módszerként idézte. (Gáspár Rezsô Debrecenben, a Kossuth Lajos Tüdományegyetem elméleti fizikai tanszékének emeritus professzora, sok évtizeden át a tanszék vezetôje).
Akár a hagyományos módszereket, akár a DFT-formalizmust tekintjük, gyakorlatilag minden mai kvantumkémiai számítás felhasználja a grádienstechnikát, melyet Pulay Péter publikált 1969-ben. Ennek az a lényege, hogy az energia mellett hatékony eljárással (analitikus deriválás) kiszámítjuk annak változását (deriváltját) az atommagok helyzete szerint. Ez nélkülözhetetlen a molekulák geometriájának meghatározásában, és kiindulási lépés bármilyen egyéb tulajdonság számításához. Ez az eredmény az egyik legfontosabb mérföldkô a kvantumkémia fejlôdésében, melynek jelentôségét nem a szerzôk magyar és személyes elfogultsága túlozza el: a Svéd Királyi Akadémia hivatalos sajtóközleménye a kémiai Nobel-díjról – amikor a háttérinformációban azt taglalja, Pople milyen eredményekre támaszkodott – összesen két nevet említ, Boys és Pulay nevét. Elôbbi a kvantumkémia elsô generációjához tartozott, s már nem él. Pulay a kitüntetetteknél is majdnem egy generációval fiatalabb korosztály képviselôje, s jelenleg is e tudományterület legsikeresebb mûvelôi közé tartozik. (Pulay Péter az ELTE-n volt a kvantumkémiai kutatások egyik úttörôje. Jelenleg az Egyesült Államokban él, a University of Arkansas professzora.)
A kvantumkémia alkalmazásai
A kvantumkémia mára valóban egyre általánosabban bevonult a kutatóvegyészek, legalábbis az alapkutatást végzô vegyészek kelléktárába, s alkalmazása nagyon sokoldalú. A következôkben csak példaként mutatunk be néhány fontosabb alkalmazási területet.
A számítógép mint szerkezetkutató "nagymûszer". A szerzõk szubjektív nézetében a kvantumkémia egyik legnagyobb haszna a szerkezetkutatásban van. A modern kémiának elengedhetetlen része a szerkezetkutatás. Ennek legelsô, s a gyakorlat szempontjából legfontosabb része a szerkezeti képlet megállapítása, de ezen túlmenôen jelentheti a részletes molekulageometria (térszerkezet) meghatározását, az elektrongerjesztések, molekularezgések, elektromos és mágneses tulajdonságok vizsgálatát stb. A szerkezetkutatásra a modern spektroszkópiai és diffrakciós "nagymûszerek" egész tárháza áll rendelkezésre, s ezekkel a fizikai módszerekkel – mint pl. az infravörös- és Raman-spektroszkópia, mágneses magrezonancia spektroszkópia (NMR), tömegspektrometria, röntgen-, ill. elektrondiffrakció – önmagukban is szinte "csodákra képes" a szerkezetkutató. A mérések kiértékelése azonban hagyományosan jórészt tapasztalati megfigyeléseken alapul. A kvantumkémiai számítások elvben lehetôvé teszik mindezen adatok elméleti kiszámítását, s így a kiértékelés sokkal megbízhatóbbá tételét. Ezen túlmenôen, a kvantumkémiai számításokkal sok esetben megkaphatók olyan adatok is, melyeket kísérletileg szinte lehetetlen lenne "elérni". A számítógép ebben az értelemben maga is szerkezetkutató "mûszer" a kvantumkémikus kezében. (Ez a gondolatsor adta jelen írás címét. Egyikünk (F. G.) pontosan 30 éve, az ifjú kutató rácsodálkozásával számolt be e lapban a kémiai szerkezetkutatás nagymûszereirôl "Fizikai módszerekkel a molekulák nyomában" címmel. Mára ilyen eszköz lett a számítógép is, mellyel a "molekulák nyomába szegôdve" kutatjuk a mikrovilágot.)
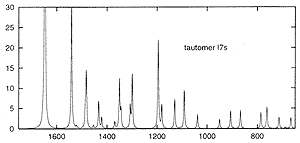
Infravörös spektrumok számítása. A spektroszkópia számos módszere közül választottuk példaként az infravörös- (IR) spektroszkópiát, mely e módszerek régi, de máig is egyik legelterjedtebb, leghatékonyabb változata. Ha egy anyagon infravörös fényt bocsátunk át, azt az anyag kisebb-nagyobb mértékben elnyeli, abszorbeálja. Az abszorpció a fény frekvenciájának függvényében változik. Az így kapott "spektrum" egy adott anyagra annyira jellemzô, hogy találóan a molekulák "ujjlenyomatának" szokták nevezni.
Az infravörös spektrum fizikai hátterében az áll, hogy egy molekulában az atomok állandó rezgô mozgást végeznek, s az infravörös fény e rezgéseket gerjeszti. A fény akkor nyelôdik el, ha frekvenciája megegyezik valamelyik molekularezgés frekvenciájával. A molekularezgések elméletileg, kvantumkémiai számításokból ma már egyre nagyobb pontossággal meghatározhatók. (E téren végzett úttörô munkát a magyarokkal kapcsolatban már említett Pulay Péter. Ilyen számítások elképzelhetetlenek a grádiensmódszer nélkül.) A számításokból nemcsak a frekvenciák, hanem az abszorpció mértéke, az infravörös intenzitások is meghatározhatók.

 |
 |
 |
| 4. ábra. Az 1-metil-adenin izomer szerkezeteinek
számított infravörös spektruma. Függõleges tengely: intenzitás (relatív skála), vízszintes tengely: hullámszám (1/cm) |
Energetikai adatok meghatározása. A kémiai folyamatok energiaváltozásokkal járnak, egy reakció irányát (az általában kisebb entrópiatagtól eltekintve) az határozza meg, hogy melyik irányban csökken az energia. Ahhoz tehát, hogy eldönthessük, bizonyos kiindulási anyagok átalakulhatnak-e más anyagokká (termékekké), elôször is az érintett molekulák energiáját kell meghatározni. Kiindulásként nézzük meg, milyen pontossággal képes a kvantumkémia az atomok energiáját meghatározni. Az 1. táblázatban feltüntettük néhány atom számított energiáját. Az alkalmazott számítási módszerek balól jobbra haladva egyre magasabb elméleti szintet jelentenek. A részletesen tárgyalt HF- és DFT-módszerek mellett feltüntettük a másodrendû perturbációszámításon alapuló ún. MP2-módszert, valamint a legmagasabb elérhetô elméleti szintet jelentô, a számítások bizonyos extrapolációját is alkalmazó ún. G2-szintet is (ez utóbbi módszert éppen Pople dolgozta ki [2b]). Láthatjuk a 1. táblázatból, hogy még a legalacsonyabb szintet jelentô HF-módszer is (százalékosan) nagyon jó eredményt ad. A kémiai reakciók során bekövetkezô energiaváltozások azonban az atomok és a molekulák teljes energiájához képest kicsik (1 hartree energia molekulánként kb. 630 kcal/mol energiának felel meg), így például a HF-szinten kapott energia pontossága nem feltétlenül elegendô kémiai célokra.
1. táblázat. Néhány atom különbözõ
kvantumkémiai módszerekkel számolt energiája
(–Eh,)* [2] alapján
*Eh (hartree) az energia atomi egysége,
1 Eh/molekula=630 kcal/mol
| Atom | HF | MP2 | DFT | G2 | egzakt |
| H | 0,4982 | 0,4982 | 0,4954 | 0,5000 | 0,5000 |
| He | 2,7552 | 2,8664 | 2,8978 | – | 2,9037 |
| Li | 7,4314 | 7,4319 | 7,4801 | 7,4322 | 7,4781 |
| C | 37,6809 | 37,7365 | 37,8320 | 37,7846 | 37,8450 |
| F | 99,3650 | 99,4890 | 99,7021 | 99,6328 | 99,7340 |
| Ne | 128,4744 | 128,6262 | 128,6262 | – | 128,9390 |
Sokkal többet mond tehát, ha a számított energiakülönbségeket tekintjük. A 2. táblázatban néhány kis molekula atomizációs energiáját tüntettük fel. Ez azt az energiát jelenti, amelyet az atomokra való felbontáshoz kellene befektetni. Látható, hogy a HF-módszer szinte használhatátlan eredményt ad, a kémiai pontosság (1–2 kcal/mol) csak a magasabb elméleti szinteken érhetô el. Az, hogy a DFT-módszer ilyen jól mûködik, magyarázza a DFT-módszer népszerûségét (a G2-számítások nagyságrendekkel több számítási kapacitástigényelnek). A táblázat adatainak körültekintô vizsgálatából persze az is látszik, hogy a G2 sokkal megbízhatóbb, a DFT pontossága egyenetlenebb, tehát használatakor körültekintôen kell eljárni.
2. táblázat. Elméleti és kísérleti atomizációs energiák (Do, kcal/mol) [2] alapján
| Atom | HF | MP2 | DFT | G2 | kísérleti |
| H2 | 75,9 | 86,6 | 103,2 | – | 103,3 |
| BeH | 48,8 | 45,3 | 53,9 | 45,5 | 46,9 |
| CH4 | 300,4 | 354,2 | 389,9 | 393,2 | 392,5 |
| H2O | 131,7 | 188,8 | 207,3 | 219,6 | 219,3 |
| CO2 | 234,7 | 381,0 | 392,9 | 384,6 | 381,9 |
| F2 | –34,3 | 36,8 | 54,4 | 36,6 | 36,9 |
Reakciódinamika. Az elméleti kémikus számára talán a legszebb, végsô feladat – túllépve az egyedi molekulák tulajdonságainak vizsgálatán – annak megértése, hogyan játszódik le a kötések felhasadásával, majd az atomok kapcsolatainak átrendezôdésével maga a kémiai reakció. Ilyenkor tehát már nemcsak az elektronok mozgására vagyunk tekintettel, hanem leírjuk az eddig rögzítettnek tekintett atommagok mozgását is. Az ilyen számítások nagy kihívást jelentenek az elmélet számára, de már vannak eredmények – igaz, csak a legegyszerûbb rendszerekre.
Illusztrációként egy, a tanszékünkön jelenleg folyó kutatásból [3] mutatunk be részletet. A szóban forgó kérdés a hipobrómossav (HOBr) molekula elbomlása ultraibolya sugárzás hatására ("fotodisszociáció"). A folyamat a magaslégkörben zajlik le, s jelentôsége abban áll, hogy ez a reakció sebességmeghatározó lehet egy, az ózon lebontását katalizáló reakcióciklusban.
A hipobrómossav fotodisszociációjának vizsgálatához
szükség van nemcsak az elektron-alapállapot, hanem gerjesztett
elektron-állapotok vizsgálatára is, hiszen a fény
hatására az elektronok magasabb energiaszintre kerülnek.
Hogy a magok mozgását is le tudjuk írni, mindkét
állapotban szükség van a molekula energiájára
az atommagok összes elrendezôdésénél. Az
ezt leíró függvény (ún. potenciálfelület)
adja
meg, hogyan változik a molekula energiája a "magkoordináták"
(az atommagok helyzetének) függvényében. Más
szavakkal ez a potenciális energia, amelyet a magok éreznek
mozgásuk során. A potenciálfelületre megbízható
eredményeket csak a kvantumkémia jelenlegi csúcsait
jelentô, legkorszerûbb – s hihetetlenül gépidô-igényes
– módszereivel lehet kapni. Az 5. ábrán látható
a HOBr-molekula alapállapotának és egyik gerjesztett
állapotának potenciálfelülete a vizsgált
reakció szempontjából releváns két koordináta
függvényében. (Meghatározásukhoz modern
munkaállomáson több mint egy hónap tiszta gépidôre
volt szükség!) Az ábrán jól látszik,
hogy az alapállapot esetében a függvény minimumot
mutat: ez felel meg a stabilis magelrendezôdésnek, azaz a
megfelelô koordinátaértékek jellemzik a molekula
geometriáját. A gerjesztett állapot potenciálfelületén
minimum nincs, a molekula ebben az állapotban disszociál.
A leegyszerûsített kép alapján is világos,
hogy mi történik a besugárzás hatására:
az elektronok magasabb energiaszintre kerülnek, ahol a magokat már
nem tartja össze az elektronfelhô. A folyamat kvantitatív
leírásához a potenciálfelület ismeretében
meg kell oldani a magokra vonatkozó (idôfüggô)
Schrödinger-egyenletet. Eredményül a magok (idôfüggô)
hullámfüggvényét kapjuk, amelybôl már
könnyen meghatározható a kémia számára
fontos reakciósebességi állandó (jelen esetben
a disszociáció sebessége), vagy az is, hogy milyen
állapotú termékek milyen arányban keletkeznek
(hatáskeresztmetszet).
 |
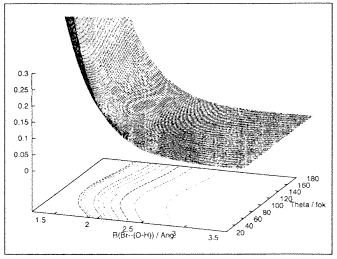 |
| 5.a ábra. A HOBr-molekula potenciálfelülete az
elektron-alapállapotban |
5.b ábra. A HOBr-molekula potenciálfelülete az
elsõ gerjesztett elektron-állapotban |
Mint látható, a reakciódinamikai számítások felhasználják azokat a módszereket, amelyek kifejlesztéséért Pople és Kohn professzor Nobel-díjat kapott, de egyben túl is lépnek ezeken, hiszen a magok mozgását is igyekeznek leírni. Az új Nobel-díjasok munkájához mérhetô erôfeszítésekre van még szükség ahhoz, hogy a kvantumkémia a reakciók tanulmányozásában is elérje azt a teljesítôképességet, amelyet mára az egyedi molekuláknál elért.
| Természet Világa, | 130. évf. 3. sz. 1999. március, 113–119. o.
https://www.kfki.hu/chemonet/TermVil/ https://www.ch.bme.hu/chemonet/TermVil/ |
| Vissza a tartalomjegyzékhez | Beszélgetés John Pople-lal 1995-ben |