Az 1998. évi Nobel-díjat megosztva John A. Pople és Walter Kohn kapta a kvantumkémia területén végzett munkájáért. A kvantumkémia a kémia egyik ága, mely elméleti alapon, számítógépes módszerekkel tanulmányozza a molekulákat annak érdekében, hogy a kémiai tulajdonságokat megértsük, s végsô célként akár tervezni tudjuk. Ez elvileg mintegy hetven éve, a kvantummechanika megalkotása óta lehetséges. Ahhoz azonban, hogy az elvi lehetôség egyre inkább gyakorlattá válhassék, évtizedek óriási elméleti-metodikai erôfeszítéseire és a számítástechnikai forradalomra volt szükség. A metodikai fejlôdés az elmúlt 3-4 évtizedben két irányban haladt: a "hagyományos" módszerek a Y hullámfüggvényre építenek, míg a sûrûségfunkcionál-elmélet (Density Functinal Theory, DFT) kísérlet arra, hogy csupán a – jóval egyszerûbb – r elektronsûrûséggel dolgozzunk. E két irány egy-egy kiemelkedô képviselôje a két kitüntetett, akiknek a következô hivatalos indoklással adományozták a Nobel-díjat: "Walter Kohnnak a sûrûségfunkcionál-elmélet kidolgozásáért és John Pople-nak a kvantumkémiai számítási módszerek kidolgozásáért."
 

John A. Pople 1925-ben született Burnham-on-Sea/Somersetben, az Egyesült Királyságban. Brit állampolgár. Matematikából szerzett PhD-fokozatot 1951-ben, Cambridge-ben. 1964-ben a kémiai fizika professzora lett a Carnegie-Mellon Universityn (Pittsburgh/USA), majd 1986-tól a kémia profeszszora a Northwestern Universityn (USA), ahol jelenleg is aktív.

Walter Kohn Bécsben született 1923-ban. 1950 és 1960 között Pittsburghben (USA), a Carnegie Insitute of Technology, majd 1960-tól 1979-ig San Diegóban, a University of California professzora. 1979 és 1984 között az Institute of Theoretical Physics/Santa Barbara igazgatója, ahol ma is dolgozik.

A kémia alapvetôen kísérleti tudomány. A vegyész – bár számos tapasztalat alapján nagyon szisztematikusan képes dolgozni s részben tervezni is – a dolog lényegét tekintve mégis szinte véletlenszerûen, 'trial and error', "próba-szerencse" elven igyekszik újabb és újabb gyógyszereket, mûanyagokat, speciális tulajdonságú anyagokat elôállítani. Jellemzô például, hogy általában sok száz vagy több ezer vegyületet kell ahhoz szintetizálni, hogy közülük akár csak egybôl is gyógyszer lehessen. Felvetôdik a kérdés, nem lehetne-e ezt a munkát szigorúbb elméleti alapra helyezni? Az elvi válasz egyértelmû: a kémiai tulajdonságokat a molekulákon belüli (intramolekuláris) és a molekulák közti (intermolekuláris) kölcsönhatások szabják meg. Ezeknek a természetét pontosan ismerjük, s igen jó közelitésben egyszerûen a töltött részecskékre, a pozitív atommagokra, ill. a negatív elektronokra vonatkozó Coulomb-törvénnyel jellemezhetjük. A leírás módjára a kvantummechanika kínál szabatos formalizmust. Ezért írhatta Dirac már 1929-ben: "A fizika nagy részének és a kémia egészének matematikai elméletéhez szükséges törvények tehát teljes egészében ismertek, és a nehézség csak abban áll, hogy e törvények egzakt alkalmazása olyan egyenletekhez vezet, melyek túl komplikáltak ahhoz, hogy megoldhatók lennének."

A kvantumkémikusok évtizedek óta azon fáradoznak, hogy sikerüljön az utóbbi problémán túllépni, s a szóban forgó egyenleteket kellô pontossággal megoldhatóvá tenni. Ahhoz, hogy e munkák lényegét megértsük, elôször megpróbáljuk szemléletes, kvalitatív képben megvilágítani a kémiai kötés mibenlétét. Ezután vázoljuk a kvantumkémia fontosabb számítási módszereit, melyeknek kifejlesztéséhez a most kitüntetett két tudós jelentôsen hozzájárult. (Érinteni fogjuk magyar kutatók meghatározó szerepét is.) Végül néhány példán illusztráljuk, hol tart ma a kémia ezen ága, melyek a jellemzô alkalmazási területek.

A kémiai kötés

Közel két évszázada annak, hogy Dalton – igen egyszerû megfigyelések alapján, a kémiai reakciókban részt vevô anyagok "súlyviszonyainak" (tömegarányainak) mérésébôl – az anyag atomos szerkezetére következtetett. Az atomok adott rend szerinti összekapcsolódása a molekula, a kémiai reakció pedig nem más, mint az atomi kapcsolatok átrendezôdése. Az a kérdés azonban, hogy milyen erôk tartják össze az atomokat a molekulákban, rejtély maradt az egész 19. század során. Nehéz is lett volna a kémiai kötést megérteni, hiszen az atom közel egy évszázadig az anyag végsô építôkövét, megbonthatatlan egységét jelentette a tudomány számára.

A kémiai kötés lényegének megértéséhez az atom belsô szerkezetének felismerésére volt szükség. Kerek száz éve, az elektron felfedezése, majd e század elején az atommag felfedezése szolgáltatta az atomra vonatkozó mai ismereteink kísérleti alapját: az atomnak szinte teljes tömege a méretéhez képest rendkívül tömör atommagban összpontosul, s e pozitív töltésû mag körül keringenek a negatív elektronok. Azonban egy ilyen rendszer a klasszikus fizika szerint képtelenség, nem lehetne stabil, mert a keringô töltés energiát sugározva be kellene essen a magba! Az atomi-molekuláris jelenségek leírásához teljesen új elméletre volt szükség. Az 1920-as évek közepén megszületett a kvantummechanika, a 20. század új világképet jelentô tudományos eredménye.

A kvantummechanika filozófiai tekintetben is teljesen új szemléletet vezetett be, melyhez valójában mindmáig nem könnyû hozzászokni. E szerint a mikrovilágban a részecskék mozgása elvileg nem követhetô nyomon olyan részletességgel, ahogyan azt a makrovilágban, hétköznapi tapasztalataink alapján megszoktuk. Szemben például a bolygók mozgásával, az atomban nincs az elektronnak a klasszikus értelemben vett pályája, mozgásáról csak statisztikus-valószínûségi kijelentés tehetô. (Ez valóban bizarr szemlélet. Nem véletlenül berzenkedett Einstein, legalábbis az értelmezés tekintetében: ,Der liebe Gott würfelt nicht' – "a Jóisten nem szerencsejátékos".)

A kvantummechanika mára teljesen megállapodott, minden kísérlettel összhangban lévô elmélete szerint egy rendszer matematikai leírását a Schrödinger-egyenlet adja:
 

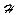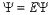(1)

Ebben a szimbolikusan tömör egyenletben a 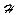 ,operátor' a Y függvényre hatva egy bonyolult differenciálegyenletet jelöl ki (E a rendszer energiája). Az atomot, molekulát a függvény jellemzi, ennek ismeretében elviekben mindent tudunk a rendszerrôl, ami a kvantummechanika szerint egyáltalán lehetséges. Szemléletes tartalma négyzetének van. Ha egyetlen elektron van az atomban (hidrogénatom), Y²(r)-rel arányos az elektron megtalálási valószínûsége a tér egy adott r pontjában. A megtalálási valószínûséget úgy is értelmezhetjük, hogy az egyelektronnyi töltés a térben felhôként oszlik szét és statisztikus átlagban Y²(r) = r(r) az elektronsûrûség. Többelektronos atomok, molekulák esetében az összes elektronra vonatkozó információt hordozza, s jelentése bonyolultabb (I. késôbb). Ilyenkor is jól definiált azonban a tér egy adott pontjában a teljes, átlagos elektronsûrûség.

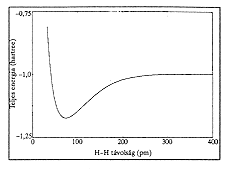1. ábra. A hidrogénmolekula ener- giája az atomtávolság függvényében

A kémiai kötés mibenlétét vizsgálhatjuk energetikai szemlélettel. A kötés ekkor azt jelenti, hogy a molekulává kapcsolódott
atomok teljes energiája kisebb, mint a szabad atomok energiájának összege: az atomok molekulává kapcsolódása energianyereséggel jár. Ez a kérdés a kvantummechanika segítségével a következõképp ragadható meg. Tekintsük a legegyszerûbb kétatomos molekulát, a hidrogént (H₂). Ha a magtávolság függvényében többször megoldjuk az (1) Schrödinger-egyenletet, az energiára az 1. ábra szerinti minimumgörbét kapjuk. Ezen "potenciálgödörben" a rendszer stabil. A végtelen távolságban lévô atomok energiájának különbsége a gödör mélyének megfelelô energia, ill. a "disszociációs energia", D_e. Az ábrához a számításokat csak demonstrációs céllal, de valójában igen pontos, "korrelációs" módszerrel (I. késôbb) végeztük. D_e számított értéke 109,1 kcal/mol, a kísérleti érték 109,4 kcal/mol. (Az egyezés gyakorlatilag tökéletessé is tehetô.)

Fentieken túl szeretnénk szemléletesen is megérteni, hogy mi tartja össze a molekulát. Errôl a kvantummechanika alapján a következô mondható. A molekula ,vázát' tehát adott (legkedvezôbb) térbeli ekendezôdésben az atommagok alkotják, s ezen pozitív töltések terében mozognak az elektronok. Az eredô átlagos elektronsûrûség túlnyomó része az atommagokon koncentrálódik, azoknak a töltését nagyrészt leárnyékolva. 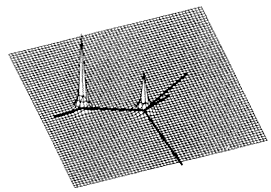A túl egyszerû H₂-nél kicsit bonyolultabb példát választva, a 2.a ábra a metil-alkohol (CH₃OH) molekulában mutatja az elektronsûrûséget olyan léptékben, hogy csak a legnagyobb értékek észlelhetôek, a szén- és az oxigénatomon. A H-atomokon a jóval kisebb maximumok ebben a léptékben nem láthatók, s még kevésbé látszik az atomok közti elektronsûrûség. 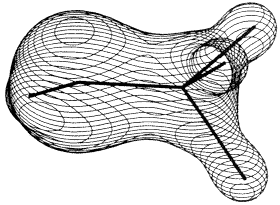A kémia szempontjából azonban az a meghatározó, hogy a teljes elektronsûrûségnek egy kicsiny, de nem elhanyagolható része az atomok közti térben koncentrálódik. A 2.b ábra a metil-alkohol elektronsûrûségének egy másik fajta, szintvonalas ábrázolása. A függvényértékeket úgy választottuk, hogy most már jól látható az elektronsûrûség az atomok közötti térrészben is: ez a negatív töltésfelhô ,ragasztja' össze a pozitív atomokat. Ebben a szemléletes megfogalmazásban tehát az atomok közti térben felhalmozódó negatív töltés az az "enyv", mely a pozitív töltésû magokat összetartja, ez jelenti a kémiai kötést.
 

2.a ábra. Elektronsûrûség-maximumok a metil-alkohol molekulában	2.b ábra. A metil-alkohol molekula elektron- sûrûségének szintvonalas ábrázolása

A kvantumkémia módszerei

A korábban szimbolikusan felírt (1) Schrödinger-egyenletet részletezve, ha N elektron mozog térben rögzített helyzetû atommagok terében, a Hamilton-operátor:

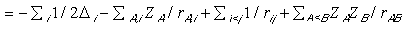(2a)

és a hullámfüggvény:

Y = Y(r1,r2,...rN) = Y(1,2,...N)

(2b)

A(2a)-ban D_i a második deriváltakból felépülô Laplace-operátor; atomi egységeket használtunk, ami azt jelenti, hogy a h Planck-állandóból adódó  = h/2p, valamint az elektron tömege és töltése egység, ezeket nem kellett kiírni; Z_A az Amag töltése (rendszáma); r_ij az i-edik és j-edik elektron távolsága; r_A,i az i-edik elektron távolsága az A magtól, r_AB az A és B mag távolsága. A (2b)-ben r_i az i-edik elektron helykoordinátáit jelöli (az elektronok spinkoordinátáit az egyszerûség kedvéért nem jelöltük); a második forma a szokásos tömörebb jelölés, mely csak indexekkel utal az elektronokra. A szokásos közelitésben az atommagok rögzítettek, ezért (2a) utolsó tagja csak egy konstans és a magkoordináták nem szerepelnek Y-ben (a magok helyzete csak egy rögzített paraméter).

Ebben az általános esetben tehát Y egy bonyolult sokváltozós függvény és Y² jelentése is összetettebb annál, amit az egyelektronos esetre fentebb elmondtunk.  Y² most a teljes elektronrendszerre vonatkozóan, az elektronok egy pillanatnyi elrendezôdését (egy adott elektroneloszlást) jellemzi.  Y²(r₁,r₂,...) annak a valószínûségével arányos, hogy az 1. elektron az r₁helyen, ugyanakkor a 2. elektron az r₂ helyen stb. tartózkodik. Ebben a fogalomban tehát benne van az elektronok mozgásának korrelációja: az, hogy milyen valószínûséggel van egy elektron adott helyen, nem adható meg önmagában, függ attól, hogy a többi elektron éppen hol van.

A Schrödinger-egyenlet a legegyszerûbb esetektôl eltekintve nem oldható meg egzakt formában. (Ez a megfogalmazás sok félreértésre adott okot. Az "egzakt" itt csak annyit jelent, hogy analitikus függvény formájában lenne megadható a megoldás. Természetesen ez nem megy, de a számítógépek korában numerikusan olyan pontossággal jellemezhetô egy függvény, hogy az analitikus alak hiánya nem feltétlenül jelent korlátozást.) Kétségtelen azonban, hogy a kvantumkémia ma alapvetôen különbözô közelítésekkel dolgozik.

A hagyományos út: Y. Ahogy azt a fentiekbôl várjuk, a kvantumkémia szokásos, "hagyományos" módszerei a Y-függvénnyel dolgoznak. A legelterjedtebb közelítés, s gyakorlatilag minden magasabb szintû számításnak is kiindulási pontja a Hartree- Fock- (HF) módszer. E modell fizikai lényege abban áll, hogy egy kiszemelt elektron a többi elektron átlagos terében mozog. Miként alább megpróbáljuk vázolni, technikailag ez arra vezet, hogy az általános sokelektronos Schrödinger-egyenlet helyett csak egy egyelektron egyenletet kell (igaz sokszor) megoldani. HF-számítások képezik az eddig végzett sok-sok (bizonyára több százezer) kvantumkémiai számítás legnagyobb részét (l. A Hartee–Fock-módszer).

A HF-modellnek jól megfogható, szemléletes tartalma van. Az elektronok "pályákon mozognak", a j_i pályán lévô elektron számára a v potenciál az a "tér", amelyet – a többi elektronnal való átlagos kölcsönhatásként – érez. Fontos azonban megjegyezni, hogy v_HF tartalma elég komplikált, pontos megértése részletesebb levezetést igényelne. Hangsúlyozzuk mindenesetre, hogy v_HF-ben a "többi elektronnal való kölcsönhatásban" az ezek által reprezentált töltéssûrûséggel való Coulomb-taszítás mellett benne van az ún. kicserélôdési effektus is. Ez utóbbi kvalitatíve annyit jelent, hogy az azonos spinû elektronok (de csak ezek) – a determináns alakú hullámfüggvénybôl kimutatható módon – a Cb-taszításon túlmenôen is "kerülik" egymást. Ezt hangsúlyozva, az alábbiak miatt a következô formális szétválasztást tesszük:
 

vHF = vCb + vx

(4c)

Visszatérve a HF-módszer gyakorlati kérdéseire, a (4) egyenletet nem differenciálegyenletként oldják meg, hanem a keresett j pályákat megfelelôen választott "bázisfüggvényekkel" (atompályák) sorbafejtve kezelik. A Fock-operátor szerepét ekkor a "Fock-mátrix" veszi át, s a probléma a számítógépeknek sokkal jobban megfelelô "mátrix sajátérték-egyenletre" vezet. Számítástechnikai szempontból a feladat igen nagyszámú integrál (a mátrixelemek) kiszámítását és tárolását, valamint a sajátérték-egyenlet (többszöri) megoldását jelenti.

Már a fent vázolt legelsô szint, a HF-módszer sem egyszerû. Nem véletlen, hogy talán két évtizede sincs, amikor Slater, a kvantumkémia egyik nagy alakja még elborzadva írt arról, hogy akár több millió integrál léphet fel a számításokban. Ezt ô még teljesen járhatatlan útnak tekintette. Szinte hihetetlen, hogy mára egy HF-számítás mégis mennyire "rutin" feladat lett. Például a fenti 2.a–2.b ábrák a szerzôk által ezen demonstrációs célra végzett Hartree-Fock számításából készültek. A metil-alkohol képlete CH₃OH, vagyis 6 atomot tartalmaz, s az elektronok száma 18. Az elvégzett közepes ab initio szintû számítás (melyben közel félmillió integrál lép fel) mindössze néhány másodpercet igényelt egy ma átlagos teljesítményûnek nevezhetô munkaállomáson. HF-szinten ma néhányszor tíz atomból álló molekulák könnyen számolhatók, s akár egy-két száz atomig lehet jelenleg felmenni. Ekkor azonban a gépidô már órákban, napokban mérhetô.

A HF-módszeren túllépô eljárásokat "korrelációs módszerek"-ként szokás emlegetni. Az a célunk, hogy az elektronok mozgásának fentebb említett korreláltságát igyekezzünk minél pontosabban figyelembe venni. Az eljárások technikája különbözô lehet, de nagyjából mindegyiknek az a lényege, hogy a (3) egyenletbeli HF egy-determináns helyett determinánsok lineáris kombinációja a hullámfüggvény:
 

Ycorr = Si ci Di

(5)

A determinánsokat úgy állitjuk elô, hogy a (4) egyenlet megoldásaiból a betöltött pályák felett adódó, D_o-ban betöltetlen "virtuális" pályákat felhasználva, egyes elektronokat magasabb pályákra teszünk.

A korrelációs számításoknak igen nagy a számításigénye, s a molekula méretének (pontosabban: az elektronok számának) magasabb (akár 6–8-adik!) hatványával nô. A korrelációs módszerek is különbözô szinteket jelentenek, a legmagasabb szintû számítások pontossága már minden igényt kielégít, de ezek 5–10 atomos molekulákra korlátozódnak. (Ilyenkor azonban Gbyte nagyságú központi memória, több tíz Gbyte diszk-kapacitás szükséges, s a gépidô a leggyorsabb gépeken is hetekben, akár hónapokban mérhetô).

A nehézségek ellenére a kvantumkémia e hagyományos útján óriási fejlôdés volt az elmúlt 30 évben. Világszerte számos kutatócsoport és sok száz kutató vett részt az elmélet fejlesztésében, s e munkák igazi vezéralakja volt John A. Pople, a Nobel-díj egyik kitüntetettje. Pople professzor sokoldalú munkájának szintézisét talán leginkább a Gaussian programcsomag jelképezi. E számítógép-program elsô verziója még 1970-ben készült el irányításával. Mára ebbôl – 30–40 kutató ,bedolgozásával' – egy kereskedelmi programcsomag lett, mely gyakorlatilag a világ minden egyetemén és számos kutatóhelyen megtalálható.

A sûrûség funkcionál-elmélet (DFT). A fent vázolt hagyományos módszer rendkívüli bonyolultságát látva, kezdetektôl fogva foglalkoztatta a kutatókat a kérdés: lehetséges-e egyszerûbb leírás? Miként említettük, ennek lényege az lenne, hogy a Y hullámfüggvény helyett a sokkal egyszerûbb r  elektronsûrûségre építsünk elméletet. Szemben a sokváltozós Y-vel, r  csak a három térkoordináta függvénye, r=r(r). Már a kvantummechanika hajnalán voltak ilyen próbálkozások (Thomas és Fermi, illetve Dirac), az 1950-es évektôl pedig Slater vezette be az ún. Xa-módszert. Ezeknek a kísérleteknek a célja azonban hangsúlyozottan az volt, hogy tovább egyszerûsítsék a már önmagában is közelítô Hartree–Fock-módszert. Új filozófiát vezetett be e kérdéskörben a most kitüntetett Walter Kohn. Elméleti eredménye egy nevezetes tétel (Hohenberg–Kohn-tétel, 1964), miszerint egy rendszert (atomot, molekulát) egyértelmûen meghatároz az alapállapotú elektronsûrûség, r(r). Utóbbiból tehát meghatározható az energia, E[r], s ez – legalábbis elvileg – nem kell, hogy közelítés legyen: ha E[r]-t ismernénk, az eredmény egzakt lenne. Ez a sûrûségfunkcionál-elmélet (DFT) alapgondolata (lásd A sûrûségfunkcionál-elmélet technikája).

A DFT-módszer technikája tulajdonképp visszatérést jelent a szokásos és fent vázolt HF-módszerhez. A (6) egyenlet teljesen analóg a (4) egyenlettel, azzal a különbséggel, hogy a Hartree-Fock-potenciál (4c)-beli v_x tagja helyett most a v_xc tag szerepel. Utóbbi a kicserélôdést és a korrelációt igyekszik egyetlen potenciállal leírni. v_xc-re különbözô formákat használnak, fizikai modelleken alapuló megfontolások, részben empirikus tapasztalatok alapján.

A DFT-módszer több évtizedes "vajúdás" után azzal vált sikeressé, hogy – bizonyos technikai (intégrálási) problémák mellett – a v_xc potenciálra a legutóbbi években sikerült egyre jobb formulákat kidolgozni. Ezáltal az eredmények meglepôen jók, kb. az egyszerûbb korrelációs közelítések pontosságát érik el, azoknál lényegesen ,olcsóbban' (kisebb számítógép-kapacitást igényelve). Így a DFT-módszer jelenleg a kvantumkémia nagy "slágere". ADFT gyakorlati sikeréhez számos kutató járult hozzá, a kitüntetett Kohn professzor érdeme a tétel megfogalmazása, mely a késôbbi munkákat inspirálta.

Folytatás