Káosz az élőközösségekben
Nemlineáris jelenségek kompetitív rendszerekben és táplálékhálózatokban
azon nem másít semmi rend,
se Isten se az ördögök:
múlónak látszik és örök.
Weöres Sándor: Öröklét (részlet)
Szinte nincs is már olyan nap, hogy a világban ne történne valahol ökológiai katasztrófa, vagy ne kapnánk hírt arról, megbomlott valamelyik térségben az ökológiai egyensúly. Az ökológia tehát hétköznapi fogalommá vált. De mivel is foglalkozik e tudomány? Kezdjük azzal, mi az ökológia alapkérdése, mivel foglalkozik az ökológus.
Induljunk ki abból a naiv feltevésből (nullhipotézisből), hogy a föld tetszőleges pontján bármely faj bármely időpontban tetszőleges mennyiségben fordul elő. Tapasztalatunk szerint ez a hipotézis hamis. Az ökológia alapkérdése az, hogy miért, és milyen mértékben hamis ez az elmélet. Kicsit kevésbé elvontan fogalmazva, az a kérdés, hogy a különböző fajok populációinak milyen együtteseit lehet megfigyelni, az együtt megfigyelhető populációk milyen mennyiségben, milyen tér- és időbeni mintázatban vannak jelen, s ami a legnehezebb, hogyan tudjuk magyarázni e megfigyeléseket (lásd folyóiratunk 1994. novemberi számát). Ökológiai egyensúlyról, illetve annak megbomlásáról éppen azért lehet beszélni, mert a fajok (különböző időskálákon) jellegzetes tér- és időbeni mintázatokban fordulnak elő.
Mit tudunk általában az ökológiai kölcsönhatásokról? Azt, hogy (és ez egyik legfontosabb tulajdonságuk) nemlineárisak. Vagyis az ökológiában a legtöbb esetben a hatás eredménye nem egyenesen arányos a hatással, két-háromszoros hatás eredménye nem lesz két-háromszoros nagyságú. Például egy populáció tényleges növekedési üteme nemcsak attól függ, hogy hány szaporodóképes egyed van a populációban, hanem például attól is, hogy milyen erős a versengés a forrásokért. Ez utóbbi mennyiség pedig az egyedszámsűrűség négyzetével arányos. Ha tehát az egyedszámsűrűség a kétszeresére nő, a forrásokért folyó versengés erőssége négyszer nagyobb lesz. Ehhez hasonlóan, a zsákmány–ragadozó, vagy gazda–parazita kölcsönhatások sem lineárisak.
Mivel a nemlineáris, viszonylag kevés változós determinisztikus dinamikai rendszerek jellegzetessége a kaotikus viselkedés (lásd folyóiratunk 1998. szeptemberi számát), várható, hogy ez a dinamikai viselkedés az ökológiai folyamatokban is szerephez jut. Azonban nem hallgatható el, hogy az élőközösségek többségében fajok tucatjaihoz tartozó egyedek állnak kapcsolatban egymással, tehát kevés változós rendszereknek ritkán tekinthetjük őket. Hasonlóan kérdéses, milyen mértékben determinisztikusak az ökológiai folyamatok. (E kérdésre az írás végén még visszatérek.) Mindezen kételyek ellenére igen sok kutató véli úgy, hogy a kaotikus jelenségeknek fontos szerepük van az ökológiai folyamatok megértésében.
A továbbiakban két alapvető fontosságú ökológiai kérdés segítségével
fogom bemutatni, hogy a kaotikus, illetve általában a nemlineáris dinamikára
jellemző tulajdonságok kulcsszerepet játszhatnak a megfigyelt ökológiai
mintázatok kialakításában. E két kérdés az ún. „planktonparadoxon”, valamint
a mindenevők szerepe a táplálékhálózatok stabilitásában.
A planktonparadoxon
Köztudott, hogy a legtöbb természetes vízben rengeteg apró egysejtű él. Sokuk számára az életműködéshez szükséges energiát a fény szolgáltatja. Ezeket az élőlényeket összefoglalóan fitoplanktonoknak nevezzük. Ha egy kora nyári napon mintát veszünk a Balaton vizéből, akkor számos, akár többtucatnyi fotoszintetizáló planktonfaj egyedeit tudjuk meghatározni. (Bevallom, én erre nem lennék képes.) A fitoplanktonsejtek növekedését és szaporodási sebességét a fény erőssége s néhány vízben oldott szervetlen anyag (például foszfor, nitrogén, széndioxid) koncentrációja befolyásolja. Tehát az együtt élő fajok száma jóval meghaladhatja a szaporodást befolyásoló tényezők számát. Igen ám, de ha ezt a folyamatot matematikailag modellezzük, arra a következtetésre jutunk, hogy az együtt élő fajok száma nem lehet több, mint az egymástól független növekedést befolyásoló (ún. limitáló) tényezők száma. Tehát a tapasztalat nem összeegyeztethető a matematikai leírás következményeivel. Ezt az ellentmondást nevezi a szakirodalom planktonparadoxonnak. A paradoxon nyilván onnan ered, hogy a matematikai modell feltevései között vannak olyanok, amelyek a valóságos folyamatokra nem illenek.
Lássuk, mit mutatnak a modellek! Az egyik legfontosabb alapfeltevés, hogy az egyedek és a növekedést meghatározó kémiai anyagok egyenletesen oszlanak el a vízben. Tehát egy jól kevert rendszert képzelünk el. Az áramló folyadékok azonban a valóságban csak ritkán tekinthetők homogénnek (jól kevertnek). Az élőlényeket és az oldott anyagokat általában bonyolult kaotikus pályákon szállítják, eloszlásuk korántsem egyenletes! Az utóbbi években számos tanulmány kimutatta, ha figyelembe vesszük a folyadékok valódi keverési tulajdonságait, számos kémiai és biológia folyamat (köztük a planktonparadoxon is) újraértelmezhető. (A sorozatban NeufeldZoltán cikke foglalkozik majd részletesen e témakörrel.) Továbbá, a matematikai leírás a környezeti fluktuációkat sem veszi tekintetbe. Vagyis nem számol például a hőmérsékleti ingadozásokkal és ciklusokkal, az alkalmanként érkező záporokkal, szélviharokkal. A sekély tavakban, mint amilyen a Balaton is, egyértelműen bizonyított, hogy az üledéket felkavaró viharoknak jelentős szerepük van a fitoplankton-közösség faji sokféleségének fenntartásában. A környezeti ingadozások tehát fontosak lehetnek a planktonparadoxon feloldásában. A harmadik, s jelen esetben részletesebben megvizsgálandó feltevés az, hogy a vizsgált matematikai modellben a forrásokért versengő (ún. kompetítor) fajok egyedszámai az idő múlásával egy-egy meghatározott egyensúlyi értékhez közelítenek (1. ábra). Mindennapi tapasztalatainkon alapuló várakozásunkkal ellentétben, a nemlineáris dinamikai rendszerek viselkedése általában ennél lényegesen összetettebb. Felvetődik tehát a kérdés: vajon a fitoplanktonrendszerek esetleges „belülről fakadó fluktuációja”, vagyis e dinamikai rendszerek esetleges kaotikus viselkedése magyarázhatja-e a fitoplankton-közösségek fajgazdagságát? A következő fejezet ezt a lehetőséget tekinti át részletesebben.
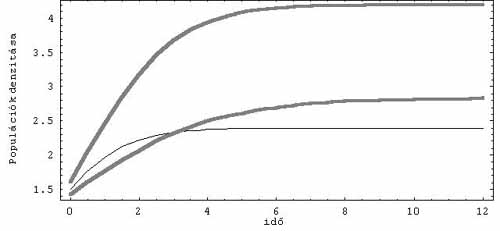
1. ábra. Stabil egyensúlyi értékhez (fixponthoz) tartó dinamika.
Három kopetítor egyedszámsűrűségének változása az idő függvényében
Planktonparadoxon és kaotikus populációk
Az ördög mindig a részletekben bújik meg. Talán éppen erre gondolt két holland kutató, Jef Huismann és Franz J. Weissing, amikor a fitoplankton-populácók versengését leíró jól ismert matematikai egyenleteket átnézték. Ahogy az előző fejezet végén rámutattam, ez a leírás számos, a probléma szempontjából lényeges ponton támadható. A kutatók egyetlen részletre koncentráltak, nevezetesen a tápanyagfelvétel matematikai leírására. Az eredeti modellekben (amelyek a planktonparadoxon kimondásához vezettek) a populációk növekedési üteme arányos a tápanyagok koncentrációjával és a populációk aktuális sűrűségének szorzatával, ráadásul a különböző tápanyagforrások egymástól függetlenül hatnak a populáció növekedésére. Az előbbi feltevés akkor igaz közelítőleg, ha tápanyagból nincs túl sok. Az utóbbi feltevés igaz lehet bizonyos esetekben, például akkor, ha egy ragadozó hal különböző fajhoz tartozó kisebb halakat fogyaszt, de a fitoplankton-közösségekre biztosan nem az. A fotoszintetizáló plankton szaporodási rátáját, illetve általában a szervetlen tápanyagokon élő élőlények gyarapodási sebességét mindig annak a szervetlen tápanyagnak a mennyisége határozza meg, amelyből hiányt szenved az élőlény. Ez a középiskolai tankönyvekben is megtalálható ún. Liebig-szabály. Tehát a fitoplankton esetében a növekedés mértékét minden időpillanatban a tápanyagforrások közül egyedül az fogja meghatározni, melyből a szükségeshez képest a legkevesebb van. Ez a feltétel a matematika nyelvére viszonylag egyszerűen lefordítható, s máris kész egy olyan modell, mely ebben a részletében pontosabb leírása a valóságnak. Ezek után nem kellett mást tenni, csupán az így kapott dinamikai rendszer viselkedését különböző paraméterek beállítása mellett számítógépen szimulálni. Az esetek egy részében semmi váratlan nem történik. Ha mondjuk három különböző forrást tételeztek föl, akkor egy, kettő vagy három faj tudott együtt élni, s az egyedszámsűrűségük (más szóval denzitásuk) valamilyen egyensúlyi értékhez tartott (1. ábra). A rendszer azonban bizonyos esetekben kaotikusan viselkedik, s ilyenkor a hosszú távon együtt élő fajok száma meghaladhatja a növekedést limitáló források számát (2. ábra). Ez akkor következhet be, ha a versengő fajok növekedését különböző források limitálják, miközben ezektől a forrásoktól más és más forrásokat aknáznak ki a leghatékonyabban. Tehát, ha például az 1. faj a 2. forrást használja ki a legjobban, de a növekedési üteme a 3. forrás mennyiségére érzékeny, a 2. faj a 3. forrást aknázza ki a leghatékonyabban, de az 1. forrás szabályozza a növekedését. Vagyis a kompetíciós viszonyokban valamilyen ciklikusság figyelhető meg.
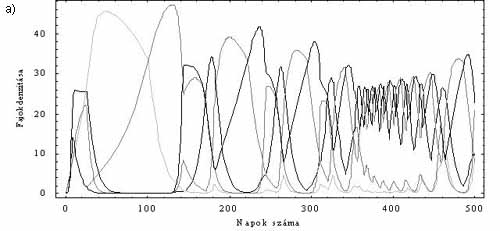
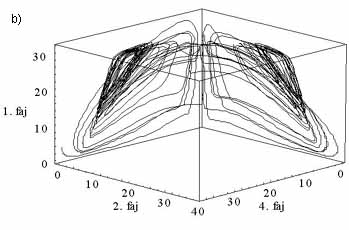
2. ábra. Három tápanyagforráson élő öt kompetítotfaj. a) Az egyedsázmsűrűségek kaotikusan változnak az időben. A különböző fajokat elétrő tónusú szüreke színezés különbözteti meg. b) Az 1., a 4. és 2. faj sűrűségének együttes változásaa kaotikus attraktoron. (Ez az ún. fázistérbeli ábrázolás.)
A részletesebb vizsgálatok során kiderült, hogy a modell viselkedése rendkívül összetett. Előfordulhat például, hogy az esetenként hosszú ideig tartó átmeneti (tranziens) kaotikus viselkedés egyszer csak megszűnik. Ezt követően csupán három faj marad életben, s az egyedszámok ciklikusan váltakoznak (3a. ábra). A kaotikus rendszerek közismert tulajdonsága, hogy a kezdeti állapotok kicsiny különbsége igen gyorsan jelentős állapotbeli eltéréseket okoz. Az már kevéssé tudott, hogy számos nemlineáris rendszerben a kezdeti értékek kicsiny változtatásával a rendszer teljesen más végállapotba kerülhet. Biológiai modellünk is ilyen. Ha a 3a. ábránál használt paramétereket megtartjuk, és csupán a kezdeti populációméreteket változtatjuk meg hajszálnyival, akkor a tranziens káoszt követően más fajok maradnak fenn, mint az előző esetben (3b. ábra). E jelenség magyarázatának lényege, hogy a 2. és 3. faj, valamint a 4. és az 5. faj külön-külön egy-egy oszcillátorpárt alkot, melyeket az 1. faj kapcsol össze. A tranziens kaotikus tartományban (a kezdeti állapottól függően) a tápanyag valamelyik faj számára tartósan túl alacsony lesz. Így ez a faj és a vele szoros kapcsolatban lévő párja kihal. E dinamikai viselkedés fontos elméleti következménye az, hogy amennyiben a modell jól írja le a valóságot, az egyes planktonközösségek fajösszetétele elvileg sem jósolható meg.
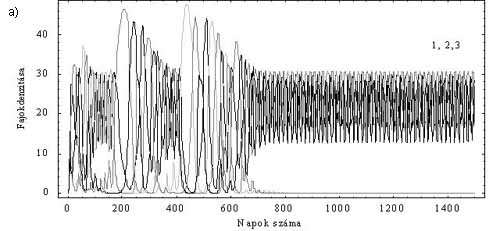
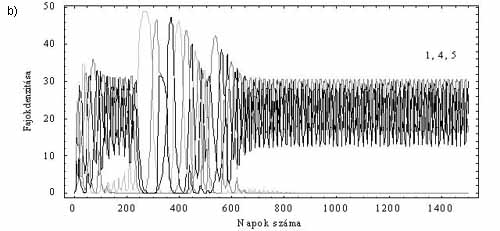
3. ábra. Tranziens káosz és érzékenység a kezdeti értékre. a) A hosszan tartó tranziens káoszt követően az 1., a 2. és a 3. faj él együtt. b) Kicsit eltérő kezdeti feltételek hatására a tranziens után az 1., a 4. és az 5.faj oszcillál
Mielőtt teljesen beleszeretnénk ebbe a dinamikai tulajdonságait tekintve igen szép modellbe, vizsgáljuk meg, mi az esélye annak, hogy a valóságban is ilyen belső dinamikai fluktuációk tartják fenn a fitoplankton-közösségek diverzitását. Láthattuk ugyanis, hogy bizonyos feltételek esetén 5 faj is együtt tudott élni 3 forráson, máskor meg csak 3 (esetleg ennél is kevesebb). Kérdés tehát, hogy a dinamikai fluktuációkból származó fajgazdagság mennyire valószínű. Átfogó számítógépes vizsgálatok eredményeként kiderült, ha a forráskihasználást és a forrásfelvételi sebességet meghatározó paramétereket véletlenszerűen válogatjuk egy-egy előre megadott tartományból, akkor az esetek igen kicsiny, kb. 0,1%-ában kapunk kaotikus s egyben fajgazdag planktonközösséget. Ha a paramétereket úgy választjuk ki, hogy a fajok azokat a forrásokat fogyasztják a leghatékonyabban, amelyektől növekedésük leginkább függ, akkor durván az esetek 11%-ában lesz a közösség kaotikus. Azonban, ha az imént említett ciklikus szabályt követjük a paraméterek válogatásánál, akkor kb. 37% lesz az esélye annak, hogy 3-nál több kaotikusan oszcilláló faj fennmaradjon. Az imént elmondott vizsgálatokat 5-8 független forrás esetén is elvégezték, és hasonló eredményekre jutottak. A döntő kérdés tehát az, hogy a fitoplankton-közösségekben milyen kapcsolat van a fajok és az egyes ökológiailag fontos tulajdonságai között. Érdekes módon, a plankton e jellemzőiről nem sokat tudunk. Annyi azért elmondható, hogy a véletlenszerű kapcsolat nagyon valószínűtlennek tűnik, míg a másik két elképzelést valamelyest a mérések is megerősítik.
Amennyiben a fitoplankton-közösségek fajgazdagságáért a rendszer viselkedéséből fakadó determinisztikus káosz a felelős, azt kéne tapasztalnunk, hogy az ilyen populációk egyedszáma kiszámíthatatlan ingadozásokat mutat (2. ábra). Valóban, az esetek többségében ez meg is figyelhető. A gond csupán az, hogy a populációk fluktuációjának számos egyéb, az előzőtől nehezen elkülöníthető oka is lehet. Egyrészt a természetes vizekben általában maguk az áramlások térben és időben is kaotikusak, másrészt a mindig jelenlévő külső környezeti fluktuációk is okozhatnak jelentős ingadozásokat a populációk méretében. Ezek az elméleti eredmények azért figyelemreméltóak, mert a planktonközösségek viselkedése laboratóriumban, szabályozott körülmények között is jól vizsgálható. Ha a fitoplankton-közösségek kaotikusak, azt a közeljövőben kísérletileg is igazolni fogják. Várjuk az erről szóló beszámolókat.
Táplálékhálózatok, mindenevők, gyenge kapcsolatok
Az olvasó joggal kérdezhetné; a fitoplankton-közösségek vizsgálatakor miért nem vettük figyelembe, hogy a planktonokat más fajok (például a zooplanktonok, puhatestűek és különböző halak) is fogyasztják. Ennek oka az, hogy a fitoplanktonoknál a predátorok hatása nem számottevő, ráadásul jelenlétük legtöbbször még növeli is a fajgazdagságot. (Hogy miért, erre nem térünk ki, mert a ragadozó általában a nagyobb tömegben előforduló táplálékot nagyobb arányban fogyasztja, így kiegyenlíti a kompetítorok közötti különbségeket.) Amennyiben egy tó, vagy tengeröböl teljes ökoszisztémájának működésére vagyunk kíváncsiak, figyelembe kell vennünk a fito-, a zooplanktont és puhatestűeket, valamint a halakat, sőt a halakkal, vízinövényekkel táplálkozó többi gerincest is. Ahhoz, hogy az élőközösség fennmaradjon, szükség van olyan fajokra, amelyek a napfény energiáját felhasználva, szervetlen anyagokból építik fel sejtjeiket. Esetünkben ezek a fitoplanktonfajok és magasabb rendű vízinövények. Ezek tehát az elsődleges szervesanyag-termelők, melyek a legalsó táplálkozási szinten helyezkednek el. Az őket fogyasztók alkotják a következő táplálkozási szintet, majd következnek a második táplálkozási szinten lévőket fogyasztó fajok, és így tovább (4a. ábra). A legtöbb élőközösségben 3–5 táplálkozási szint különíthető el. (Ennek oka önmagában is izgalmas probléma.) A legtöbb faj a közvetlenül alatta lévő táplálkozási szinthez tartozó fajokat fogyasztja, de vannak kivételek is. Ezek a fajok a mindenevők vagy omnivórok(4b. ábra). A legismertebb mindenevő az ember, de vízközeli példánknál maradva, gondolhatunk szinte bármely ragadozó halra. A kis méretű ivadékhalak leginkább planktonokkal, később inkább kisebb halakkal (köztük saját fajtársaikkal is) táplálkoznak, miközben rovarokat, apró rákokat is fogyasztanak.

4. ábra. Táplálékhálózatok felépítése. a) Egy egyszerű táplálékhálózat. Az egyes szinteken több faj is lehet. b) Az előbbi hálózat, de a csúcsragadozó mindenevő
Az ökológusokat régóta foglalkoztatja az a kérdés, hogy a táplálékhálózatok szerkezetében milyen általános összefüggéseket lehet fölfedezni. Megfigyelték például, hogy egyes táplálékhálózatokban egyáltalán nincsenek mindenevők, míg más esetekben a mindenevők aránya igen magas is lehet (például a ragadozók csaknem fele ilyen). Felvetődik tehát a gyanú, hogy a mindenevők egyes hálózattípusok esetén a rendszer együtt-tartásáért felelősek, máskor éppen ellenkező a szerepük. Természetesen az omnivória sok esetben azért ritka, mert a különböző táplálkozási szinteken élő fajok elejtéséhez és/vagy megemésztéséhez egész más testfelépítésre, emésztőrendszerre stb.-re lenne szükség. Például a madaraknál a csőr felépítése nagyban meghatározza, hogy az állat magokkal vagy rovarokkal táplálkozik-e.
E nyilvánvaló kényszerfeltételek hatásától függetlenül, a ma már klasszikusnak tekinthető elméleti vizsgálatok leginkább arra a következtetésekre vezettek, hogy a mindenevők nagymértékben csökkentik a hálózat stabilitását. Pontosabban, azt sikerült a modellek segítségével kimutatni, hogy a mindenevők arányának növelésével rohamosan csökken azon hálózatok aránya, ahol egyensúlyban az összes faj denzitása valamilyen meghatározott pozitív értéket vesz fel. Emlékezzünk vissza arra, hogy a planktonközösségek vizsgálatakor is ez volt az egyik megkérdőjelezhető föltevés (1. ábra).
Természetesen a táplálékhálózatok is nemlineáris rendszerek, ezért dinamikai viselkedésük sokoldalú és összetett. Ezért Kevin McCann és Alan Hastings (amerikai elméleti ökológusok) a közelmúltban újra górcső alá vették ezt a kérdést. Olyan egyszerű táplálékhálózatokat vizsgáltak, ahol egy elsődleges szervesanyag-termelő, egy növényevő és egy ragadozó faj alkotta a hálózatot (4a. ábra). Azonban a fajok közötti kölcsönhatásokat a korábbi modelleknél lényegesen pontosabban vették figyelembe, ráadásul a tereptapasztalatok alapján a modell paramétereire is tudtak nagyságrendi becsléseket adni. Megmutatták, hogy ez a hálózat lehet kaotikus, előfordulhat tranziens káosz, a határciklus (itt a denzitások ciklikusan változnak), és esetenként a populációk stabil egyensúlyba is juthatnak.
Ezek után feltették, hogy a csúcsragadozó bizonyos arányban fogyasztja az elsődleges szervesanyag-termelőt is, tehát így ő már mindenevőnek számít (4b. ábra). A módosított modellben egyetlen paraméter értéke határozta meg, hogy milyen mértékben volt a ragadozó mindenevő. Például, ha ez az érték 0,1, akkor a mindenevő az energiaszükségletének 10%-át szerzi be a legalsó táplálkozási szintről. Így tehát azt is vizsgálni tudták, hogy a „mindenevőség” mértéke hogyan hat a táplálékhálózat viselkedésére. Legnagyobb meglepetésükre a nem túl erős mindenevő táplálkozási mód általában a populációk minimális méretét növelte, ráadásul kaotikus fluktuációk kialakulásának a lehetőségét is csökkentette (5. ábra). Ha a minimális populációméret növekszik, csökken az esélye annak, hogy egy faj valamilyen külső zavar miatt kipusztuljon, s ezzel esetleg az egész hálózat összeomoljon. Tehát a mindenevők egyrészt „védik” a táplálékhálózatot a külső zavarástól, másrészt csökkentik a kaotikus viselkedés kialakulásának esélyét is. Az imént elmondottak akkor nem igazak, amikor a mindenevők hiányában a hálózat stabil egyensúlyi értéket vesz fel. Éppen ez az a dinamikai eset, melyet a klasszikus vizsgálatok előtérbe helyeztek. Utóbb az is kiderült, hogy nemcsak a mindenevőknek lehet általában ilyen stabilizáló, hálózat-összetartó szerepe, hanem általában is igaznak tűnik, hogy a fajok közötti néhány gyengébb kölcsönhatás dinamikailag stabilizál és védelmet nyújt a környezeti fluktuációkkal szemben.
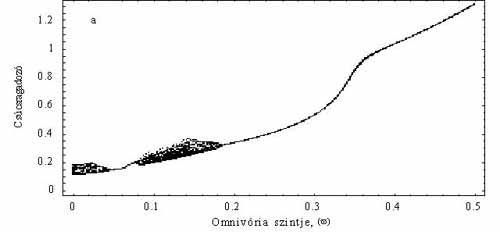
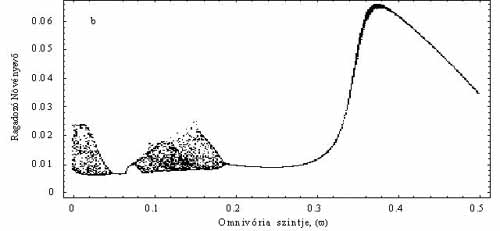
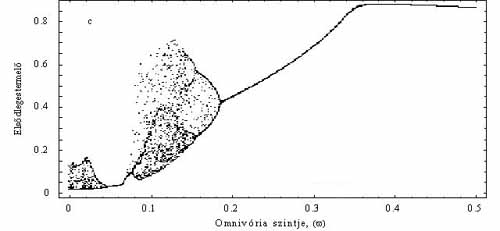
5. ábra. A mindenevő hatása, ha a táplálékhálózat kaotikus. Az x tengelyen az omnivória mértéke (w), az y tengelyen egy meghatározott időintervallumban mért legkisebb populációsűrűségek láthatóak. Ha az w nagyon kicsi, vegy egyáltalán nincs omnivória, akkor mindhárom populáció kaotikusan fluktuál. A paraméter növelésével előbb periodikusak lesznek a populációk (pl. 0,1 < w < 0,2), majd stabil egyensúlyi értéket vesznek fel (w > 0,2). Tehát egy gyenge, de nem elhanyagolható omnivória a hálózat egésze szemponjtából kedvező
A számos megválaszolatlan kérdés miatt az imént vázolt eredmények némi fenntartással kezelendők. Nem tudjuk például, hogy a gyenge kölcsönhatások stabilizáló szerepe mennyire jelentős a valósághoz közelebb álló nagyobb hálózatokban. Ráadásul egy igen új vizsgálat rámutatott arra, hogy a zsákmány-ragadozó kapcsolatot leíró matematikai összefüggések csekély (de biológiailag megalapozott) módosítása a hálózat dinamikai viselkedését, és a gyenge kölcsönhatások szerepét alapvetően megváltoztatja. A vizsgált modellek egytől egyik feltételezik, hogy a környezeti fluktuációk és a periodikus (évszakos, napi) változások elhanyagolhatóak. Vajon igazak maradnak-e a következtetések, ha ettől a feltevéstől eltekintünk?
Sajnos a nemlineáris rendszerek alaptulajdonsága, hogy a rendszerben történő kicsiny változtatás a viselkedésben jelentős minőségi változást okoz. Ezért, ha nehezünkre esik is, bele kell törődnünk, hogy egy-egy eseti vizsgálatból nemigen lehet túlzottan általános következtetéseket levonni.
Kitekintés
Ahogy azt a cikk elején már kifejtettük, a vizsgált ökológiai rendszereket úgy képzeljük el, hogy a résztvevők mozgása folyamatosan és tökéletesen elkeveri azokat. A valóságban azonban az egyedek egyes helyeken nagyobb sűrűségben, máshol ritkábban fordulnak elő. Mozgásuk élőhelyükön sokféle lehet. Szállíthatja őket víz (fitoplankton), szél, esetleg az állatok (edényes növények spórái, pollenje, magok), vagy mozoghatnak aktívan, saját mozgásszervük segítségével. Tehát az ökológiai folyamatok leírásához általában a térbeli folyamatokat is modellezni kell.
Képzeljük el, hogy egy ragadozó és egy lehetséges zsákmánya él egy területen. A ragadozó aktívan keresi a zsákmányt, az áldozat viszont menekülni próbál. A modellek szerint gyakran megtörténik, hogy mind a ragadozó, mind a zsákmány egyedeinek sűrűsége kaotikusan változik a terület egyazon kiválasztott részletén, de ha egyazon időpillanatban megvizsgáljuk az egész területen az egyedsűrűségeket, akkor is egymástól eltérő kaotikusan változó értékeket fogunk mérni. A rendszer időben és térben is kaotikusan viselkedik. Az észak-európai pocok- és lemmingpopulációk adatsorai azt sugallják, hogy ilyen kaotikus hullámok a valóságban is megjelennek.
Természetesen a térbeli folyamatok figyelembevételével még a legegyszerűbb élőközösség esetén sem mondhatjuk, hogy kevés változó határozza meg a populációk viselkedését, hiszen a számos lokális térrészlet kölcsönhatása alakítja ki ezt az összetett mintázatot. Továbbá, ahogy azt korábban már jeleztem, a mindig jelenlévő véletlenszerű környezeti hatások miatt csak erős jóindulattal tételezhető fel, hogy az ökológiai rendszerekben a kölcsönhatások determinisztikusak. Tehát az ökológiai rendszerek inkább sokváltozósak, s a külső zajnak általában fontos szerep jut.
Igyekeztem érzékeltetni azt is, hogy a kölcsönhatásokban felfedezett apró, részletbeni eltérések merőben eltérő viselkedést okozhatnak. Sajnos ezekről a részletekről az esetek döntő többségében semmit sem tudunk. Az elméleti ökológusok – talán a hagyományok, talán a kényelem miatt – a populációk méreteit folytonosan változó mennyiségeknek tekintik. Pedig tudjuk, hogy ez sem igaz, hiszen az erdőben élhet 10, 173 vagy 2018 szarvas, de például Ö–8 soha. Domokos Gábor e sorozatban megjelenő írása pont az ilyen típusú dinamikai rendszerek korántsem nyilvánvaló viselkedését mutatja be.
Az elmondottak alapján, a cikkben bemutatott érdekes eredményeknek kissé ellentmondva, megállapítható, hogy az ökológiában az alacsonydimenziós determinisztikus káosz nyilván nem lehet túl gyakori jelenség. Amit biztosan tudunk az, hogy nemlineáris rendszerekkel van dolgunk, melyek magukon viselik azok alapvető jellegzetességét, a komplexitást. Többek között ezért olyan izgalmas tudomány az elméleti ökológia.
Köszönetnyilvánítás
Köszönöm Domokos Gábornak és Tél Tamásnak segítő szándékú észrevételeiket
és tanácsaikat. Ezt a munkát a T032423-as és a T037726-os számú OTKA-pályázatok
támogatják. A szerző a Bolyai-ösztöndíj támogatásában is részesül.
Irodalom
Huisman J. and Weissing F. J. (2001) Fundamental unpredictability in
multispecies competition. The American Naturalist 157, 488–494
McCann K. and Hastings A. (1997) Re-evaluating the omnivory-stability
relationship in food webs. Proceedings of Royal Society B 264, 1249–1254
McCann K., Hastings A., Huxel G. R. (1998) Weak trophic interactions
and the balance of nature. Nature 395, 794–798
Pimm S. (1982) Food webs. London: Chapman & Hall.
Scheuring I. (1994) Gondolatok az ökológia törvényszerűségeiről: In
memoriam Juhász-Nagy Pál. Természet Világa 125,11: 503–507
Scheuring I. (1998) Kaotikus
jelenségek a biológiában. Természet Világa 129: 8, 338–342.
Tél T. (1998) A káosz temészetrajza.
Természet Világa 129,9: 386–388
| Természet Világa, | 133. évfolyam, 8. szám, 2002. augusztus
https://www.chemonet.hu/TermVil/ https://www.kfki.hu/chemonet/TermVil/ |
Vissza a tartalomjegyzékhez